
26. In many ways China’s rapid growth has been seen as a(n) _______ to improve the cooperation with other countries.
A. motivation B. attempt C. conception D. realization
25. _______ was known to all, perseverance is a kind of quality and that’s ______ it takes to do anything well.
A. As; which B. As; what C. It; which D. It; what
24. Many new workers _______ trained and in two months they will _______ to build a new railway.
A. are; be sending B. are being; be sent C. are; send D. will be; be to send
23. This is a very special flower and it can _______a strong sweet perfume at night.
A. given in B. give up C. give out D. give over
22.--What’s up, Mike? You look pale.
--Oh, I’m not feeling well in the stomach. I _______so much fried chicken just now.
A. shouldn’t eat B. mustn’t have eaten
C. shouldn’t have eaten D. mustn’t eat
第一节 单项填空(共15小题,每小题1分,满分15分)
从A. B. C. D 四个选项中选出可以填入空白处的最佳选项。
21. She reckons that you should have ______ minimum of three exercise classes a week to get any of _______benefits.
A. a; \ B. \;the C. the; the D. a; the
20. 已知等差数列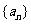 中,公差
中,公差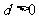 ,其前
,其前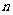 项和为
项和为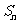 ,且满足
,且满足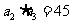 ,
,
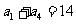 .
.
(1)求数列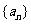 的通项公式;
的通项公式;
(2)设由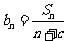 (
(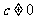 )构成的新数列为
)构成的新数列为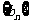 ,求证:当且仅当
,求证:当且仅当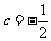 时,数列
时,数列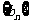 是等差数列;
是等差数列;
(3)对于(2)中的等差数列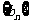 ,设
,设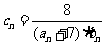 (
(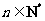 ),数列
),数列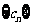 的前
的前
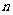 项和为
项和为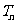 ,现有数列
,现有数列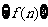 ,
,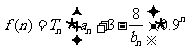 (
(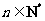 ),
),
是否存在整数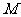 ,使
,使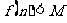 对一切
对一切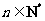 都成立?若存在,求出
都成立?若存在,求出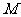 的最小
的最小
值,若不存在,请说明理由.
解:(1)∵等差数列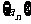 中,公差
中,公差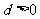 ,
,
∴ (2分)
(2分)
(2)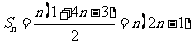 ,
,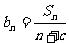
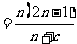 ,
(4分)
,
(4分)
由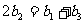 得
得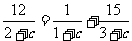 ,化简得
,化简得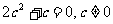 ,∴
,∴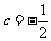 (5分)
(5分)
反之,令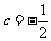 ,即得
,即得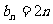 ,显然数列
,显然数列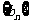 为等差数列,
为等差数列,
∴
当且仅当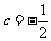 时,数列
时,数列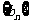 为等差数列.
(8分)
为等差数列.
(8分)
(3)
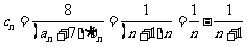
∴
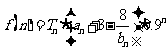
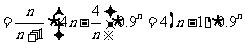 ( 10分)
( 10分)

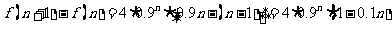
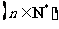
∴当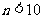 时,
时,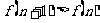 ,当
,当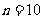 时,
时,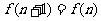 ,当
,当 时,
时,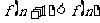 ,∴
,∴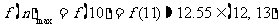 (13分)
(13分)
21已知函数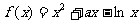 ,
,
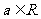
(1)若函数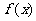 在
在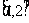 上是减函数,求实数
上是减函数,求实数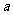 的取值范围;
的取值范围;
(2)令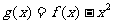 ,是否存在实数
,是否存在实数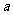 ,当
,当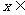
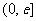 (
(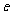 是自然常数)时,函数
是自然常数)时,函数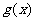 的最小值是3,若存在,求出
的最小值是3,若存在,求出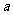 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)当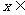
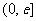 时,证明:
时,证明: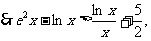
21已知函数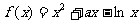
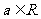
(1)若函数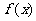 在
在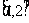 上是减函数,求实数
上是减函数,求实数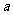 的取值范围;
的取值范围;
(2)令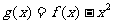 ,是否存在实数
,是否存在实数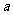 ,当
,当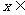
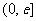 (
(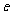 是自然常数)时,函数
是自然常数)时,函数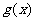 的最小值是3,若存在,求出
的最小值是3,若存在,求出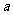 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)当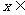
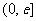 时,证明:
时,证明: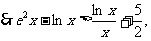
[解析]:(1)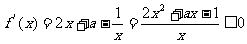 在
在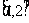 上恒成立,
上恒成立,
令 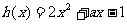 ,有
,有 得
得 ………
………
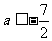 ………………………………………………………
5分
………………………………………………………
5分
(2)假设存在实数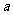 ,使
,使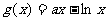 (
(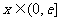 )有最小值3,
)有最小值3,
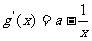
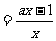 ………………………………6分
………………………………6分
①
当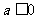 时,
时,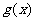 在
在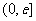 上单调递减,
上单调递减,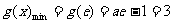 ,
,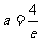 (舍去),
(舍去),
②当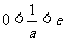 时,
时,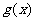 在
在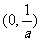 上单调递减,在
上单调递减,在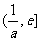 上单调递增
上单调递增
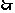
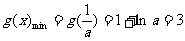 ,
,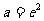 ,满足条件.
,满足条件.
③当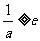 时,
时,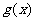 在
在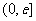 上单调递减,
上单调递减,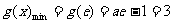 ,
,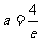 (舍去),
(舍去),
综上,存在实数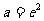 ,使得当
,使得当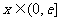 时
时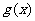 有最小值3. …………………10分
有最小值3. …………………10分
(3)令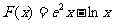 ,由(2)知,
,由(2)知,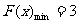 .令
.令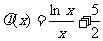 ,
,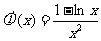 ,
,
当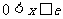 时,
时,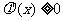 ,
,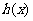 在
在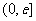 上单调递增
上单调递增
∴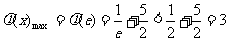 :
:
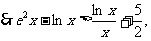 .………14分
.………14分
19. 某化工厂打算投入一条新的生产线,但需要经环保部门审批同意方可投入生产,已知该厂连续生产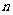 个月的累计产量为
个月的累计产量为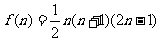 吨,但如果产量超过96吨,将会给环境造成危害.
吨,但如果产量超过96吨,将会给环境造成危害.
(1)请你代表环保部门给厂拟定最长的生产周期;
(2)若该厂在环保部门的规定下生产,但需要每月交纳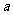 万元的环保税,已知每吨产品售价
万元的环保税,已知每吨产品售价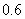 万元,第
万元,第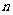 个月的工人工资为
个月的工人工资为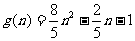 万元,若每月都赢利,求出
万元,若每月都赢利,求出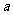 的范围.
的范围.
解:(1)第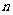 个月的月产量=
个月的月产量=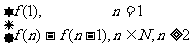 .
.
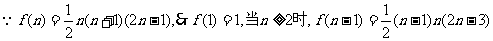 ,
,
 .
.
令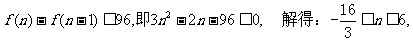
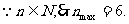
(2)若每月都赢利,则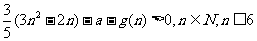 恒成立.
恒成立.
即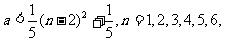 恒成立,则
恒成立,则
令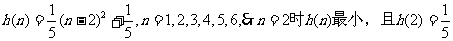
所以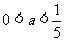 .
.
解:(1)第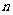 个月的月产量=
个月的月产量=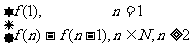 .
.
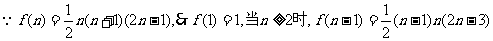 ,
,
 .
.
令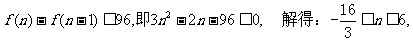
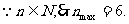
(2)若每月都赢利,则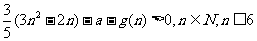 恒成立.
恒成立.
即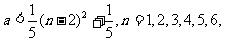 恒成立,则
恒成立,则
令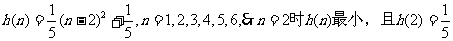
所以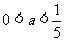 .
.
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com