
5、某班学生在一次数学考试中成绩分布如下表:
|
分数段 |
[0,80) |
[80,90) |
[90,100) |
[100,110) |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
|
人数 |
2 |
5 |
6 |
8 |
12 |
6 |
4 |
2 |
那么分数在[100,110)中的频率和分数不满110分的累积频率分别是(精确到0.01)………( )
A、0.08,0.47 B、0.47,0.18 C、0.18,0.50 D、0.38,0.75
4、某校有高一学生300人,高二学生270人,高三学生210人,现教育局督导组欲用分层抽样的方法抽取26名学生进行问卷调查,则下列判断正确的是……………………………………( )
A、高一学生被抽到的概率最大 B、高三学生被抽到的概率最大
C、高三学生被抽到的概率最小 D、每名学生被抽到的概率相等。
3、一个容量为20的样本数据,分组后组距与频数如下:(10,20],2;(20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70],2. 则样本在区间(-50,50]上的频率为……( )
A、5% B、25% C、50% D、70%
1、袋中有40个小球,其中红色球16个、蓝色球12个、白色球8个、黄色球4个,从中随机抽取10个球作成一个样本,则这个样本恰好是按分层抽样方法得到的概率为………………( )
A、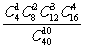 B、
B、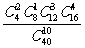 C、
C、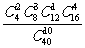 D、
D、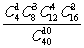
23.已知函数 (
(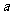 为实常数)
为实常数)
(1)若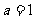 ,作函数
,作函数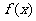 的图像;
的图像;
(2)设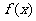 在区间
在区间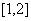 上的最小值为
上的最小值为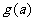 ,求
,求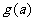 的表达式:
的表达式:
(3)设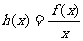 ,若函数
,若函数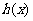 在区间
在区间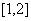 上是增函数,求实数
上是增函数,求实数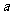 的取值范围.
的取值范围.
22.斜率为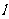 的直线过抛物线
的直线过抛物线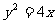 的焦点,且与抛物线交于两点
的焦点,且与抛物线交于两点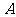 、
、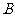 .
.
(1)求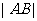 的值;
的值;
(2)将直线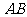 按向量
按向量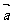 =(-2,0)平移得直线
=(-2,0)平移得直线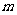 ,
,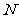 是
是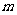 上的动点,求
上的动点,求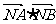 的最小值.
的最小值.
(3)设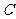 (2,0),
(2,0),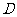 为抛物线
为抛物线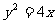 上一动点,证明:存在一条定直线
上一动点,证明:存在一条定直线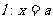 ,使得
,使得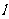 被以
被以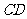 为直径的圆截得的弦长为定值,并求出直线
为直径的圆截得的弦长为定值,并求出直线 的方程.
的方程.
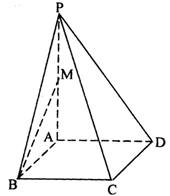
21.如图,在四棱锥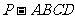 中,底面
中,底面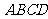 是边长为2的菱形,∠
是边长为2的菱形,∠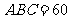 °,
°,
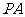 ⊥平面
⊥平面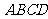 ,
,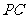 与平面
与平面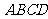 所成角的大小为
所成角的大小为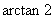 ,
,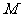 为
为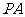 的中点.
的中点.
(1)求四棱锥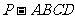 的体积;
的体积;
 (2)求异面直线
(2)求异面直线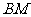 与
与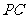 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
20.已知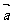 =
=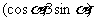 ,
,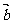 =
=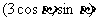 ,
,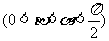 是平面上的两个向量
是平面上的两个向量
(1)试用 、
、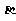 表示
表示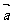 ·
·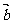 .
.
(2)若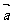 ·
·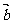 =
=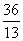 ,且
,且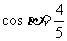 ,求
,求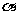 的值.(结果用反三角函数值表示)
的值.(结果用反三角函数值表示)
19.设数列{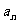 }的前
}的前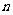 项和为
项和为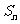 ,
,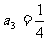 .对任意
.对任意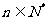 ,向量
,向量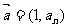 ,
,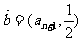 满足
满足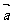 ⊥
⊥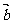 ,求
,求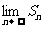 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com