
(一)选择题:
1、(07全国Ⅰ)已知向量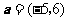 ,
,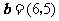 ,则
,则 与
与 ( )
( )
A、垂直 B、不垂直也不平行 C、平行且同向 D、平行且反向
2、(07上海)直角坐标系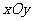 中,
中,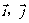 分别是与
分别是与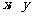 轴正方向同向的单位向量.在直角三角形
轴正方向同向的单位向量.在直角三角形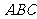 中,若
中,若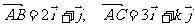 ,则
,则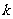 的可能值个数是( )
的可能值个数是( )
A、1 B、2 C、3 D、4
3、(07辽宁)若向量 与
与 不共线,
不共线,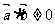 ,且
,且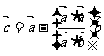 ,则向量
,则向量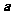 与
与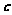 的夹角为( )
A、0 B、
的夹角为( )
A、0 B、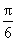 C、
C、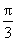 D、
D、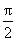
4、(07湖南)设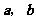 是非零向量,若函数
是非零向量,若函数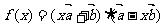 的图象是一条直线,则必有( ) A、
的图象是一条直线,则必有( ) A、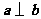 B、
B、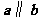 C、
C、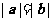 D、
D、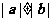
5、(06北京)若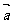 与
与 都是非零向量,则“
都是非零向量,则“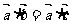 ”是“
”是“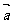
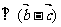 ”的( )
”的( )
A、充分而不必要条件 B、必要而不充分条件
C、充分必要条件 D、既不充分也不必要条件
6、(06江苏)已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,满足
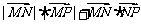 =0,则动点P(x,y)的轨迹方程为( )
=0,则动点P(x,y)的轨迹方程为( )
A、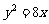 B、
B、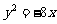 C、
C、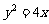 D、
D、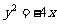
7、(06湖南)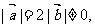 且关于
且关于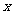 的方程
的方程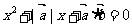 有实根, 则
有实根, 则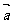 与
与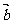 的夹角的取值范围是( )
的夹角的取值范围是( )
A、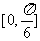 B、
B、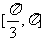 C、
C、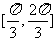 D、
D、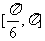
8、(06重庆)与向量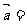
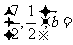
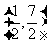 的夹解相等,且模为1的向量是( )
的夹解相等,且模为1的向量是( )
A、 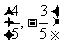 B、
B、
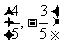 或
或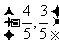
C、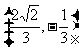 D、
D、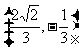 或
或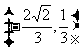
9、(05北京)| a |=1,| b |=2,c = a + b,且c⊥a,则向量a与b的夹角为( )
A、30° B、60° C、120° D、150°
10、(05全国Ⅱ)点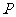 在平面上作匀速直线运动,速度向量
在平面上作匀速直线运动,速度向量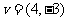 (即点
(即点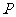 的运动方向与
的运动方向与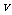 相同,且每秒移动的距离为
相同,且每秒移动的距离为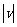 个单位).设开始时点
个单位).设开始时点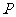 的坐标为
的坐标为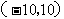 ,则5秒后点
,则5秒后点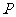 的坐标为
的坐标为
A、(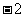 ,4) B、(
,4) B、(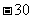 ,25) C、(10,
,25) C、(10,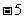 ) D、(5,
) D、(5,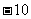 )
)
例1、(07山东)在直角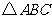 中,
中,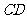 是斜边
是斜边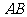 上的高,则下列等式不成立的是( )
上的高,则下列等式不成立的是( )
A、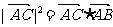 B、
B、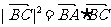
C、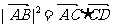 D.
D.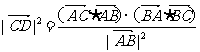
例2、(06浙江)设向量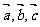 满足
满足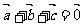 ,
,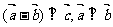 若
若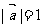 ,则|
,则|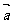 |
|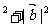 +
+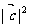 的值是 ;
的值是 ;
例3、(05江苏)在△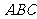 中,
中, 为中线
为中线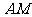 上的一个动点,若
上的一个动点,若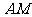 =2,则
=2,则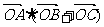 的最小值是
;
的最小值是
;
例4、(05山东)已知向量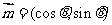 和
和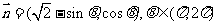 ,且
,且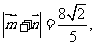 求
求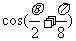 的值。
的值。
(二)填空题:
10、 (07江西)如图,在
(07江西)如图,在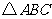 中,点
中,点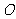 是
是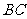 的中点,过点
的中点,过点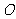 的直线分别交直线
的直线分别交直线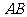 ,
,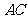 于不同的两点
于不同的两点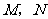 ,若
,若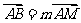 ,
,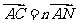 ,则
,则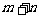 的值为 ;
的值为 ;
11、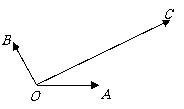 (07陕西)如图,平面内有三个向量
(07陕西)如图,平面内有三个向量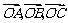 ,其中
,其中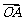 与
与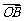 的夹角为
的夹角为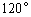 ,
,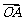 与
与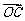 的夹角为
的夹角为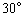 ,且
,且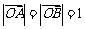 ,
,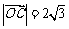 .若
.若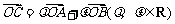 ,则
,则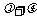 的值为
的值为
;
12、(06北京)若三点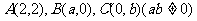 共线,则
共线,则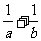 的值等于 ;
的值等于 ;
13、(05天津)在直角坐标系xOy中,已知点A (0,1)和点B (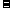 3,4),若点C在∠AOB的平分线上且
3,4),若点C在∠AOB的平分线上且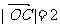 ,则
,则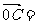 __________。
__________。
(一)选择题:
1、(07海南)已知平面向量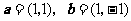 ,则向量
,则向量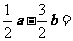 ( )
( )
A、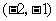 B、
B、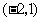 C、
C、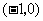 D、
D、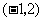
2、(07福建)对于向量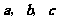 和实数
和实数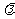 ,下列命题中真命题是( )
,下列命题中真命题是( )
A、若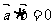 ,则
,则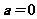 或
或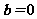 B、若
B、若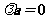 ,则
,则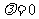 或
或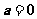
C、若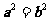 ,则
,则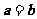 或
或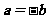 D、若
D、若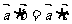 ,则
,则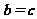
3、(07浙江)若非零向量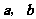 满足
满足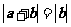 ,则( )
,则( )
A、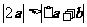 B、
B、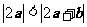 C、
C、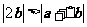 D、
D、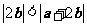
4、(07四川)设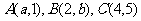 ,为坐标平面上三点,O为坐标原点,若
,为坐标平面上三点,O为坐标原点,若
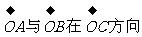 上的投影相同,则
上的投影相同,则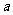 与
与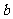 满足的关系式为( )
满足的关系式为( )
A、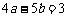 B、
B、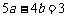 C、
C、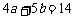 D、
D、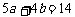
5、(07上海春)如图,平面内的两条相交直线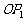 和
和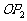 将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界)
将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界) 若
若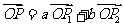 ,且点
,且点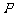 落在第Ⅲ部分,则实数
落在第Ⅲ部分,则实数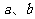 满足
满足 ( )
( )
A、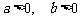 B、
B、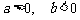
C、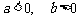 D、
D、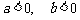
6、 (06广东)如图所示,
(06广东)如图所示,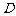 是
是 的边
的边 上的中点,则向量
上的中点,则向量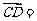 ( )
( )
A、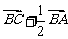 B.、
B.、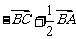
C、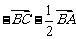 D、
D、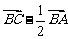
7、(06山东)设向量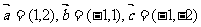 ,若表示向量
,若表示向量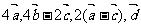 的有向线段首尾相连能构成四边形,则向量
的有向线段首尾相连能构成四边形,则向量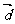 为( )
为( )
A、(2,6) B、(-2,6) C、(2,-6) D、(-2,-6)
8、(06辽宁)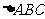 的三内角
的三内角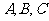 所对边的长分别为
所对边的长分别为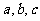 设向量
设向量
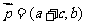 ,
, ,若
,若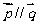 ,则角
,则角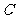 的大小为( )
的大小为( )
A、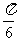 B、
B、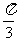 C、
C、 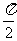 D、
D、 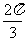
9、(05山东)已知向量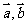 ,且
,且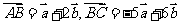 ,
,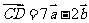 ,则一定共线的三点是( )
,则一定共线的三点是( )
A、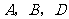 B、
B、 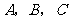 C、
C、 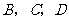 D、
D、 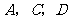
例1、(08上海春)已知向量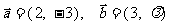 ,若
,若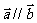 ,则
,则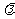 等于( )
等于( )
A、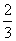 B、
B、 C、
C、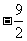 D、
D、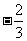
例2、(07天津)设两个向量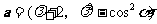 和
和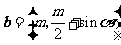 ,其中
,其中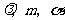 为实数.若
为实数.若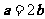 ,则
,则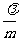 的取值范围是( )
的取值范围是( )
A、[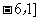 B、
B、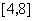 C、
C、 D、
D、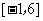
例3、(07全国Ⅱ)在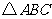 中,已知
中,已知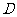 是
是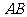 边上一点,若
边上一点,若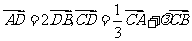 ,则
,则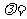 ( )
( )
A、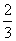 B、
B、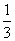 C、
C、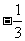 D、
D、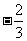
例4、(06全国Ⅰ)设平面向量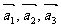 的和
的和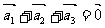 。如果向量
。如果向量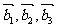 满足
满足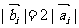 ,且
,且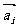 顺时针旋转
顺时针旋转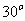 后与
后与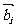 同向,其中
同向,其中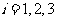 ,则( )
,则( )
A、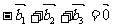 B、
B、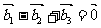
C、 D、
D、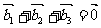
例5、(06安徽)在平行四边形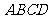 中,
中,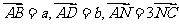 ,
,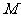 为
为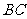 的中点,则
的中点,则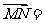 _______。(用
_______。(用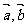 表示)
表示)
例6、(05全国Ⅲ)已知向量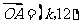 ,
,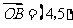 ,
,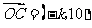 ,且
,且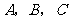 三点共线,则
三点共线,则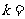 ;
;
例7、(05上海22)在直角坐标平面中,已知点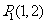 ,
,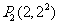 ,
,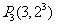 ,…,
,…,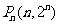 ,其中
,其中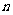 是正整数.对平面上任一点
是正整数.对平面上任一点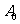 ,记
,记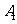 为
为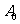 关于点
关于点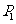 的对称点,
的对称点,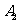 为
为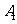 关于点
关于点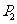 的对称点,……,
的对称点,……,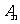 为
为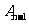 关于点
关于点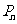 的对称点。(1)求向量
的对称点。(1)求向量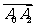 的坐标;(2)当点
的坐标;(2)当点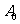 在曲线
在曲线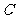 上移动时,点
上移动时,点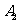 的轨迹是函数
的轨迹是函数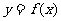 的图象,其中
的图象,其中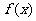 是以3为周期的周期函数,且当
是以3为周期的周期函数,且当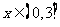 时,
时,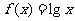 ,求以曲线
,求以曲线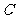 为图象的函数在
为图象的函数在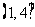 的解析式;(3)对任意偶数
的解析式;(3)对任意偶数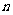 ,用
,用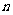 表示向量
表示向量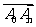 的坐标。
的坐标。
[解](1)设点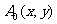 ,A0关于点P1的对称点A1的坐标为
,A0关于点P1的对称点A1的坐标为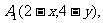
A1关于点P2的对称点A2的坐标为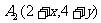 ,所以,
,所以,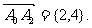
(2)[解法一]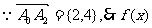 的图象由曲线C向右平移2个单位,再向上平移
的图象由曲线C向右平移2个单位,再向上平移
4个单位得到.
因此,基线C是函数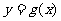 的图象,其中
的图象,其中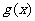 是以3为周期的周期函数,且当
是以3为周期的周期函数,且当

[解法二]设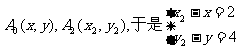
若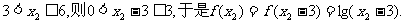
当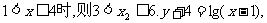
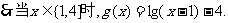
(3)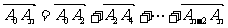
由于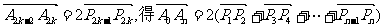 ,
,
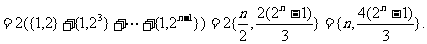
18.暑假不补课,我们却怀念校园中结伴玩乐的情景;平时上学时,我们又期盼早点放假。我们在矛盾中成长着。矛盾是我们人生绕不过的弯,有的人在矛盾面前迷惘了人生的方向,有的人在矛盾中学会了选择,有的人在解决矛盾中长大,而在有的人看来,这所谓的矛盾并不是矛盾。
请以“矛盾,成长的音符”为题,写一篇不少于800字的文章。
要求:①角度自选;②立意自定;③除诗歌外,文体自选。
语文Ⅱ(加试题)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com