
3.在数列{an}中,如果存在非零常数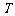 ,使得am+T =am对于任意的非零自然数
,使得am+T =am对于任意的非零自然数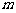 均成立,那么就称数列{an}为周期数列,其中
均成立,那么就称数列{an}为周期数列,其中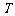 叫数列{an}的周期。已知数列{xn}满足xn+1=|xn–xn-1|(n≥2),如果x1=1,x2=a(a∈R,a≠0),当数列{xn}的周期最小时,该数列前2005项的和是
叫数列{an}的周期。已知数列{xn}满足xn+1=|xn–xn-1|(n≥2),如果x1=1,x2=a(a∈R,a≠0),当数列{xn}的周期最小时,该数列前2005项的和是
A.668 B.669 C.1336 D.1337
2.根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量Sn(万件)近似地满足Sn=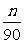 (21n-n2-5)(n=1,2,……,12),按此预测,在本年度内,需求量超过1.5万件的月份是
(21n-n2-5)(n=1,2,……,12),按此预测,在本年度内,需求量超过1.5万件的月份是
A.5月、6月 B.6月、7月 C.7月、8月 D.8月、9月
1.若数列{an}前8项的值各异,且an+8=an对任意n∈N*都成立,则下列数列中可取遍{an}前8项值的数列为
A.{a2k+1} B.{a3k+1} C.{a4k+1} D.{a6k+1}
23. (本小题满分10分)设函数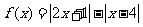 .
.
(I)解不等式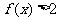 ;
;
(II)求函数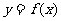 的最小值.
的最小值.
22.(本小题满分10分)如图,⊙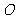 的直径
的直径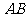 的延长线与弦
的延长线与弦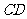 的延长线
的延长线
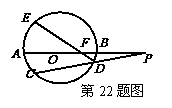 相交于点
相交于点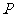 , D
, D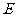 为⊙O上一点,
为⊙O上一点,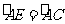 ,
,
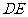 交
交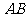 于点
于点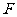 ,且
,且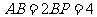 ,
,
求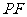 的长度.
的长度.
21. (本小题满分12分) 已知函数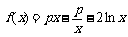 .
.
⑴ 若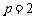 ,求曲线
,求曲线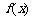 在点
在点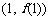 处的切线方程;
处的切线方程;
⑵ 若函数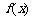 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
⑶ 设函数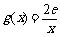 ,若在
,若在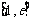 上至少存在一点
上至少存在一点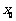 ,使得
,使得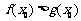 成立,求实数
成立,求实数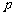 的取值范围.
的取值范围.
选做题:从下列22~23两小题中任选做一小题,如果两小题都做,则只按前一小题记分
20. (本小题满分12分)如图,已知抛物线方程为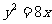 。
。
⑴直线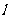 过抛物线的焦点F,且垂直于x轴,
过抛物线的焦点F,且垂直于x轴,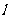 与抛物线交于
与抛物线交于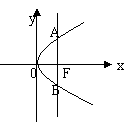 A、B两点,
A、B两点,
求AB的长度。
⑵直线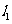 过抛物线的焦点
过抛物线的焦点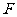 ,且倾斜角为
,且倾斜角为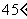 ,直线
,直线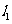 与抛
与抛
物线相交于C、D两点,O为原点。求△OCD的面积。
19.(本小题满分12分)如图所示,在棱长为2的正方体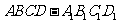 中,
中,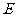 、
、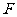 分别为
分别为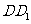 、
、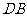 的中点.
的中点.
(Ⅰ)求证: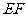 //平面
//平面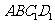 ;
;
(Ⅱ)求证: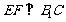 ;
;
(Ⅲ)求三棱锥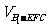 的体积.
的体积.
18. (本小题满分12分)把一颗骰子投掷两次,第一次出现的点数记为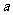 ,第二次出现的点数记为
,第二次出现的点数记为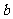 。已知直线
。已知直线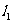 :
: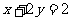 ,直线
,直线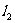 :
: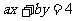 ,试求:(Ⅰ)直线
,试求:(Ⅰ)直线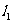 、
、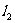 相交的概率; (Ⅱ)直线
相交的概率; (Ⅱ)直线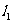 、
、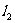 平行的概率;
平行的概率;

17. (本小题满分12分) 设函数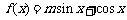
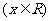 的图象经过点
的图象经过点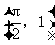 .(Ⅰ)求
.(Ⅰ)求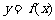 的解析式,并求函数的最小正周期和最值.
的解析式,并求函数的最小正周期和最值.
(Ⅱ)若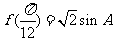 ,其中
,其中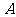 是面积为
是面积为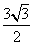 的锐角
的锐角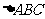 的内角,且
的内角,且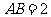 ,
,
求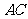 和
和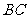 的长.
的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com