
(二)填空题:
3、(06上海)三个同学对问题“关于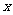 的不等式
的不等式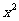 +25+|
+25+|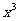 -5
-5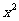 |
|
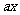 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数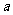 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量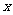 的函数,右边仅含常数,求函数的最值”.
的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于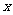 的函数,作出函数图像”.
的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即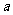 的取值范围是
的取值范围是
(一)选择题:
1、(06全国Ⅰ)用长度分别为2、3、4、5、6(单位: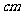 )的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为( )
)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为( )
A、 B、
B、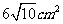 C、
C、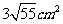 D、
D、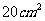
2、(06江西)若不等式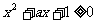 对于一切
对于一切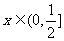 成立,则
成立,则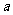 的取值范围是( )
的取值范围是( )
A、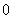 B、
B、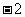 C、
C、 D、
D、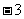
例1、(05湖南)集合 ,若“a=1”是“
,若“a=1”是“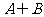 ≠
≠ ”的充分条件, 则
”的充分条件, 则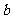 的取值范围是( )
的取值范围是( )
A、-2≤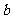 <0 B、0<
<0 B、0<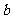 ≤2 C、-3<
≤2 C、-3<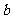 <-1 D、-1≤
<-1 D、-1≤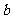 <2
<2
例2、(05山东)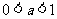 ,下列不等式一定成立的是( )
,下列不等式一定成立的是( )
A、 B、
B、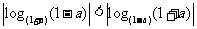
C、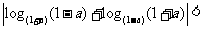
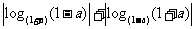
D、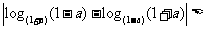
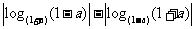
例3、(05北京春19)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量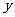 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度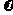 (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为: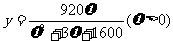 。
。
(1)在该时段内,当汽车的平均速度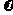 为多少时,车流量最大?最大车流量为多少?(精确到
为多少时,车流量最大?最大车流量为多少?(精确到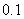 千辆/小时)
千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车站的平均速度应在什么范围内?
例4、(04福建21)已知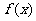 =
=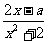 (x∈
(x∈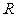 )在区间[-1,1]上是增函数。(Ⅰ)求实数
)在区间[-1,1]上是增函数。(Ⅰ)求实数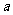 的值所组成的集合
的值所组成的集合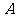 ;(Ⅱ)设关于x的方程
;(Ⅱ)设关于x的方程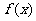 =
=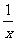 的两个非零实根为x1、x2.试问:是否存在实数
的两个非零实根为x1、x2.试问:是否存在实数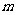 ,使得不等式
,使得不等式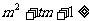
 对任意
对任意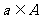 及
及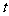 ∈[-1,1]恒成立?若存在,求
∈[-1,1]恒成立?若存在,求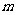 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
解:(Ⅰ)f'(x)=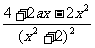 =
= 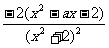 ,
,
∵f(x)在[-1,1]上是增函数,
∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立. ①
设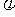 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一:
① 
 -1≤a≤1,
-1≤a≤1,
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}. 方法二:
①
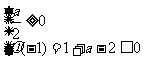 或
或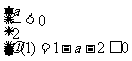
 0≤a≤1
或 -1≤a≤0
0≤a≤1
或 -1≤a≤0
 -1≤a≤1.
-1≤a≤1.
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
(Ⅱ)由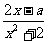 =
=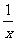 ,得x2-ax-2=0, ∵△=a2+8>0
,得x2-ax-2=0, ∵△=a2+8>0
∴x1,x2是方程x2-ax-2=0的两非零实根,x1+x2=a,x1x2=-2,
从而|x1-x2|=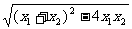 =
=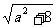 .
.
∵-1≤a≤1,∴|x1-x2|= ≤3.
≤3.
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立. ②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:
②  g(-1)=m2-m-2≥0,g(1)=m2+m-2≥0,
g(-1)=m2-m-2≥0,g(1)=m2+m-2≥0,
 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
方法二:
当m=0时,②显然不成立;
当m≠0时,
② m>0,g(-1)=m2-m-2≥0 或 m<0,g(1)=m2+m-2≥0
m>0,g(-1)=m2-m-2≥0 或 m<0,g(1)=m2+m-2≥0
 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}。
(一)选择题:
1、(06江苏)设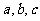 是互不相等的正数,则下列等式中不恒成立的是
是互不相等的正数,则下列等式中不恒成立的是
(A)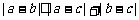 (B)
(B)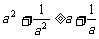
(C)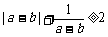 (D)
(D)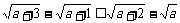
2、(06陕西)已知集合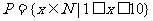 ,集合
,集合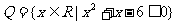 , 则
, 则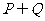 等于( )
A.、{2} B、{1,2} C、{2,3} D、{1,2,3}
等于( )
A.、{2} B、{1,2} C、{2,3} D、{1,2,3}
3、(06江西)若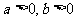 ,则不等式
,则不等式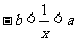 等价于( )
等价于( )
A、 或
或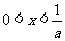 B、
B、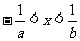
C、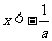 或
或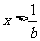 D、
D、 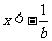 或
或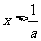
4、(04北京)已知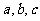 满足
满足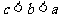 ,且
,且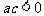 ,那么下列选项中一定成立的是(
)
,那么下列选项中一定成立的是(
)
A、 B、
B、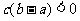 C、
C、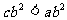 D、
D、
5、(04湖北)若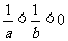 ,则下列不等式①
,则下列不等式①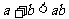 ;②
;②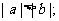 ③
③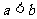 ;④
;④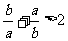 中,正确的不等式有( )
中,正确的不等式有( )
A、1个 B、2个 C、3个 D、4个
6、(04上海)某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
|
行业名称 |
计算机 |
机械 |
营销 |
物流 |
贸易 |
|
应聘人数 |
215830 |
200250 |
154676 |
74570 |
65280 |
|
行业名称 |
计算机 |
营销 |
机械 |
建筑 |
化工 |
|
招聘人数 |
124620 |
102935 |
89115 |
76516 |
70436 |
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是( )
A、计算机行业好于化工行业 B、建筑行业好于物流行业
C、机械行业最紧张 D、营销行业比贸易行业紧张
例1、(06上海春)
例2、(04湖北)若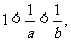 则下列结论中不正确的是( )
则下列结论中不正确的是( )
A、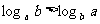 B、
B、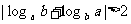
C、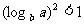 D、
D、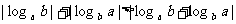
例3、(04辽宁)对于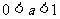 ,给出下列四个不等式:
,给出下列四个不等式:
①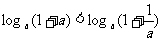 ②
②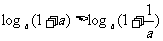
③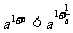 ④
④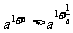 其中成立的是( )
其中成立的是( )
A、①与③ B、①与④ C、②与③ D、②与④
(二)填空题:
7、(05重庆)集合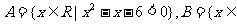 R|
R| 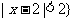 ,则
,则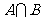 = ;
= ;
8、(06江苏)不等式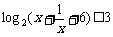 的解集为
;
的解集为
;
9、(07浙江)不等式 的解集是
。
的解集是
。
(一)选择题:
1、(04重庆)不等式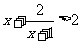 的解集是( )
的解集是( )
A 、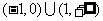 B、
B、
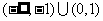
C 、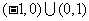 D、
D、
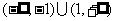
2、(05上海)已知集合 ,
,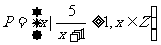 ,则
,则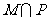 等于( )
等于( )
A、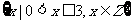 B、
B、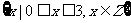
C、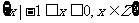 D、
D、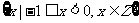
3、(06全国Ⅰ)设集合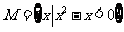 ,
,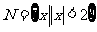 ,则( )
,则( )
A、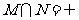 B、
B、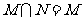 C、
C、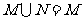 D、
D、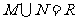
4、(06山东)设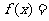
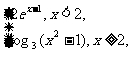
 则不等式
则不等式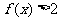 的解集为( )
的解集为( )
A、(1,2) (3,+∞)
B、(
(3,+∞)
B、(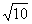 ,+∞)
,+∞)
C、(1,2)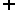 (
(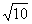 ,+∞) D、(1,2)
,+∞) D、(1,2)
5、(07湖南)不等式 的解集是( )
的解集是( )
A、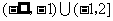 B、
B、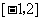 C、
C、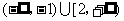 D、
D、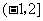
6、(07全国Ⅱ)不等式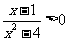 的解集是( )
的解集是( )
A、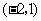 B、
B、 C、
C、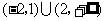 D、
D、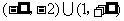
例1、(07上海春)若关于x的不等式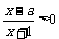 的解集为
的解集为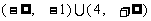 ,则
,则
实数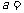 ;
;
例2、(06上海春)不等式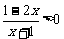 的解集是
;
的解集是
;
例3、(05福建)已知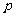 :
: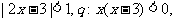 则
则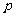 是
是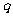 的( )
的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
例4、(05江西)已知函数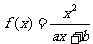 (a,
(a,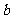 为常数)且方程
为常数)且方程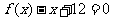 有两个实根为
有两个实根为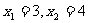 。
。
(1)求函数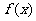 的解析式;
的解析式;
(2)设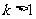 ,解关于x的不等式;
,解关于x的不等式;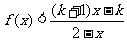 。
。
[思路点拨]本题主要考查求函数的解析式及含参分式不等式的解法.
[正确解答](1)将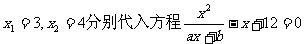 得
得
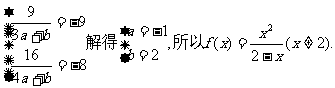
(2)不等式即为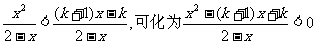
即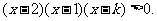
①当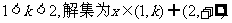
②当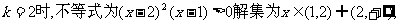
③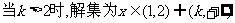 .
.
[解后反思]解不等式的过程实质上就是转化的过程,分式不等式转化成整式不等式,解分式不等式一般情况下是移项,通分,然后转化成整式不等式,对于高次不等式,借助数轴法,则简单,快捷,另外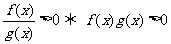 ,
,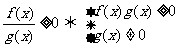
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com