
4. 已知命题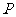 :
: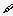
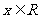 ,使得
,使得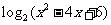 ≤
≤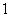 ,那么
,那么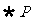 是( )
是( )
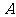 .
.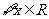 ,都有
,都有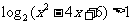 ;
; 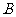 .
.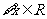 ,使得
,使得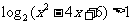 ;
;
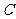 .
.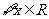 ,都有
,都有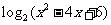 ≤
≤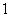 ;
; 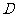 .
.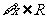 ,使得
,使得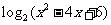 ≤
≤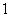 .
.
3、已知 函数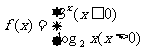 ,那么
,那么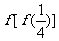 的值为 ( )
的值为 ( )
A. 9
B.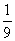 C.
C.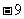 D.
D.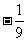
2、判断下列各组中的两个函数是同一函数的为( )
⑴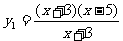 ,
,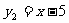 ;⑵
;⑵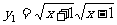 ,
,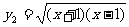 ;
;
⑶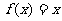 ,
,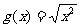 ; ⑷
; ⑷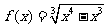 ,
,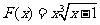 ;
;
⑸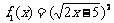 ,
,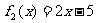

A ⑴、⑵ B
⑴、⑵ B ⑵、⑶ C
⑵、⑶ C ⑷ D
⑷ D ⑶、⑸
⑶、⑸
1、集合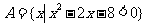 ,集合
,集合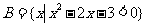 ,则
,则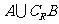 是( )
是( )
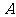 .
.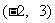
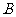 .
.
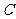 .
.
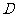 .
.
(二)填空题:
7、(07海南)某校安排5个班到4个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排一个班,不同的安排方法共有 种;(用数字作答)
8、(07辽宁)将数字1,2,3,4,5,6拼成一列,记第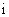 个数为
个数为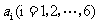 ,若
,若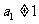 ,
,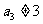 ,
,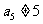 ,
,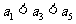 ,则不同的排列方法有 种(用数字作答);
,则不同的排列方法有 种(用数字作答);
9、(07陕西)安排3名支教教师去6所学校任教,每校至多2人,则不同的分配方案共有
种;(用数字作答)
10、(07江苏)某校开设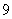 门课程供学生选修,其中
门课程供学生选修,其中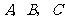 三门由于上课时间相同,至多选一门,学校规定,每位同学选修
三门由于上课时间相同,至多选一门,学校规定,每位同学选修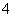 门,共有_____种不同的选修方案.(用数值作答)
门,共有_____种不同的选修方案.(用数值作答)
11、(07浙江)某书店有11种杂志,2元1本的8种,1元1本的3种,小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是 (用数字作答);
12、(07湖南)将杨辉三角中的奇数换成1,偶数换成0,得到如图1所示的0-1三角数表.从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第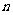 次全行的数都为1的是第 行;第61行中1的个数是 ;
次全行的数都为1的是第 行;第61行中1的个数是 ;
第1行 1 1
第2行 1 0 1
第3行 1 1 1 1
第4行 1 0 0 0 1
第5行 1 1 0 0 1 1
…… ………………………………………
13、(06江苏)今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有 种不同的方法(用数字作答)。
(一)选择题:
1、(07北京)记者要为5名志愿都和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( )
A、1440种 B、960种 C、720种 D、480种
2、(07四川)用数字0,1,2,3,4,5可以组成没有重复数字,并且比20000大的五位偶数共有( )
A、288个 B、240个 C、144个 D、126个
3、(06山东)已知集合A={5},B={1,2},C={1,3,4},从这三个集合中各取一个元素构成空间直角坐标系中点的坐标,则确定的不同点的个数为
A、33 B、34 C、35 D、36
4、(06湖南)某外商计划在4个候选城市投资3个不同的项目, 且在同一个城市投资的项目不超过2个, 则该外商不同的投资方案有
A、 16种 B、36种 C、42种 D、60种
5、(06天津)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )
A、10种 B、20种 C、36种 D、52种
6、(05全国Ⅰ)过三棱柱任意两个顶点的直线共15条,其中异面直线有( )
A、18对 B、24对 C、30对 D、36对
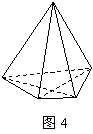 例1、(07广东)如果一个凸多面体是
例1、(07广东)如果一个凸多面体是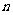 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条,这些直线中共有
棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条,这些直线中共有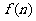 对异面直线,则
对异面直线,则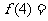 ;
;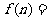 .(答案用数字或
.(答案用数字或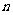 的解析式表示)
的解析式表示)
例2、(07全国Ⅱ)从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有( )
A、40种 B、60种 C、100种 D、120种
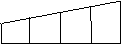 例3、(07天津)如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有 种(用数字作答).
例3、(07天津)如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有 种(用数字作答).
例4、(06全国Ⅰ)设集合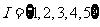 。选择
。选择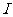 的两个非空子集
的两个非空子集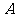 和
和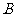 ,要使
,要使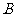 中最小的数大于
中最小的数大于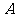 中最大的数,则不同的选择方法共有( )
中最大的数,则不同的选择方法共有( )
A、50种 B、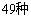 C、48种
D、47种
C、48种
D、47种
(三)解答题:
12、(07四川22)设函数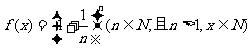 .
.
(Ⅰ)当x=6时,求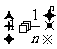 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数x,证明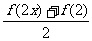 >
>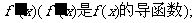
(Ⅲ)是否存在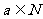 ,使得
,使得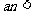
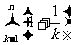 <
<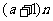 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由。
恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由。
(Ⅰ)解:展开式中二项式系数最大的项是第4项,这项是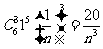
(Ⅱ)证法一:因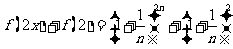
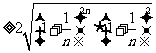
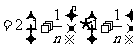
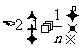
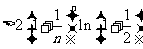
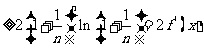
证法二:因为
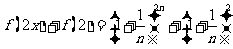

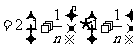
而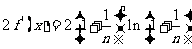
故只需对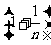 和
和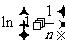 进行比较。
进行比较。
令 ,有
,有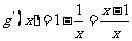
由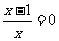 ,得
,得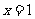
因为当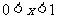 时,
时,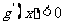 ,
,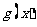 单调递减;当
单调递减;当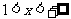 时,
时,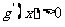 ,
,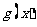 单调递增,所以在
单调递增,所以在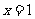 处
处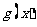 有极小值
有极小值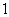
故当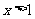 时,
时,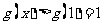 ,
,
从而有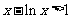 ,亦即
,亦即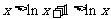
故有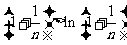 恒成立。
恒成立。
所以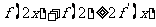 ,原不等式成立。
,原不等式成立。
(Ⅲ)对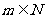 ,且
,且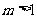
有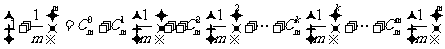
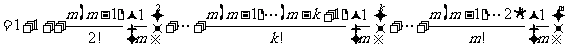
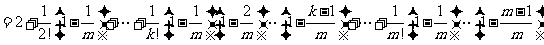
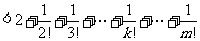
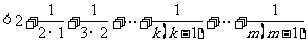

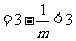
又因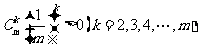 ,故
,故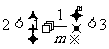
∵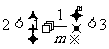 ,从而有
,从而有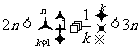 成立,
成立,
即存在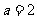 ,使得
,使得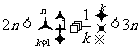 恒成立。
恒成立。
(二)填空题:
8、(07天津)若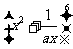 的二项展开式中
的二项展开式中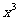 的系数为
的系数为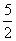 ,则
,则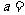 (用数字作答);
(用数字作答);
9、(06全国Ⅱ)在(x4+)10的展开式中常数项是 (用数字作答);
10、(06广东)在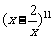 的展开式中,
的展开式中,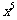 的系数为________;
的系数为________;
11、(05全国Ⅰ)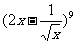 的展开式中,常数项为 (用数字作答)。
的展开式中,常数项为 (用数字作答)。
(一)选择题:
1、(07湖北)如果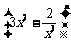 的展开式中含有非零常数项,则正整数
的展开式中含有非零常数项,则正整数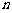 的最小值为( )
的最小值为( )
A、3 B、5 C、6 D、10
2、(07重庆)若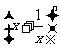 展开式的二项式系数之和为
展开式的二项式系数之和为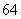 ,则展开式的常数项为( )
,则展开式的常数项为( )
A、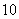 B、
B、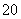 C、
C、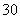 D、
D、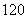
3、(07江西)已知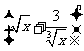 展开式中,各项系数的和与其各项二项式系数的和之比为
展开式中,各项系数的和与其各项二项式系数的和之比为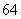 ,则
,则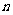 等于( ) A、
等于( ) A、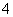 B、
B、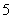 C、
C、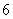 D、
D、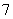
4、(06山东)已知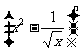 的展开式中第三项与第五项的系数之比为-
的展开式中第三项与第五项的系数之比为-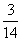 ,其中
,其中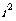 =-1,则展开式中常数项是( )
=-1,则展开式中常数项是( )
A、-45i B、 45i C、 -45 D、45
5、(06江苏)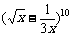 的展开式中含
的展开式中含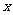 的正整数指数幂的项数是( )
的正整数指数幂的项数是( )
A、0 B、2 C、4 D、6
6、(06浙江)若多项式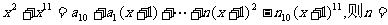 ( )
( )
A、9
B、10
C、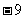 D、
D、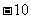
7、(06湖北)在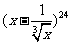 的展开式中,
的展开式中,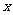 的幂的指数是整数的项共有( )
的幂的指数是整数的项共有( )
A、3项 B、4项 C、5项 D、6项
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com