
7、⑴证明:当a>1时,不等式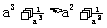 成立。
成立。
⑵要使上述不等式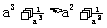 成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由。
成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由。
⑶请你根据⑴、⑵的证明,试写出一个类似的更为一般的结论,且给予证明。
解:(1)证: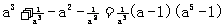 ,∵a>1,∴
,∵a>1,∴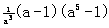 >0,
>0,
∴原不等式成立 (6¢)
(2)∵a-1与a5-1同号对任何a>0且a¹1恒成立,∴上述不等式的条件可放宽
为a>0且a¹1 (9¢)
(3)根据(1)(2)的证明,可推知:若a>0且a¹1,m>n>0,则有 (12¢)
(12¢)
证:左式-右式= (14¢)
(14¢)
若a>1,则由m>n>0Þam-n>0,am+n>0Þ不等式成立;
若0<a<1,则由m>n>0Þ0<am-n<1, 0<am+n<1Þ不等式成立.(16¢)
6、已知函数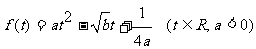 的最大值为正实数,集合
的最大值为正实数,集合
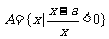 ,集合
,集合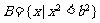 。
。
(1)求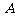 和
和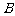 ;
;
(2)定义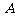 与
与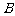 的差集:
的差集: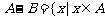 且
且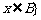 。
。
设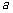 ,
,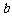 ,
,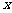 均为整数,且
均为整数,且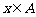 。
。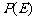 为
为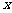 取自
取自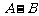 的概率,
的概率,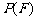 为
为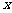 取自
取自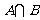 的概率,写出
的概率,写出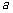 与
与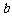 的二组值,使
的二组值,使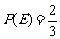 ,
,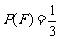 。
。
(3)若函数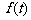 中,
中,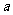 ,
,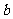 是(2)中
是(2)中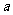 较大的一组,试写出
较大的一组,试写出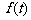 在区间[
在区间[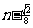 ,n]上的最大值函数
,n]上的最大值函数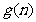 的表达式。
的表达式。
解:(1)∵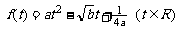 ,配方得
,配方得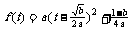 ,由
,由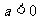 得最大值
得最大值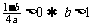 。……………………………………………………………3分
。……………………………………………………………3分
∴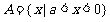 ,
,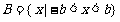 。…………………………6分
。…………………………6分
(2)要使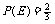 ,
,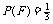 。可以使①
。可以使①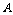 中有3个元素,
中有3个元素,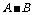 中有2个元素,
中有2个元素, 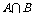 中有1个元素。则
中有1个元素。则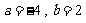 。…………………………………………………9分
。…………………………………………………9分
②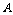 中有6个元素,
中有6个元素,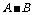 中有4个元素,
中有4个元素, 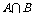 中有2个元素。则
中有2个元素。则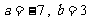 …………………………………………………………………………12分
…………………………………………………………………………12分
(3)由(2)知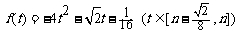 …………………………13分
…………………………13分
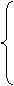
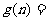
 ………………………………………………18分
………………………………………………18分
5、已知两个向量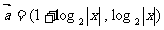 ,
,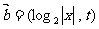
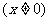 .
.
(1)若t=1且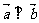 ,求实数x的值;.
,求实数x的值;.
(2)对tÎR写出函数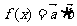 具备的性质.
具备的性质.
解:(1)由已知得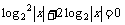 ……2分
……2分
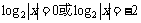 ……4分
……4分
解得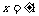 ,或
,或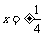 ……6分
……6分
(2)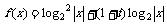 ……8分
……8分
具备的性质:
①偶函数;
②当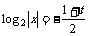 即
即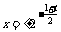 时,
时,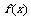 取得最小值
取得最小值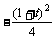 (写出值域为
(写出值域为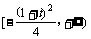 也可);
也可);
③单调性:在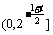 上递减,
上递减,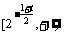 上递增;由对称性,在
上递增;由对称性,在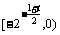 上递增,在
上递增,在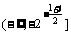 递减
……14分
递减
……14分
说明:写出一个性质得3分,写出两个性质得5分,写出三个性质得6分,包括写出函数的零点(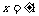 ,
, )等皆可。写出函数的定义域不得分,写错扣1分
)等皆可。写出函数的定义域不得分,写错扣1分

.
4、(理)已知
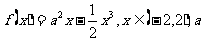 为正常数。
为正常数。
(1)可以证明:定理“若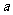 、
、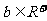 ,则
,则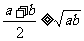 (当且仅当
(当且仅当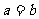 时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
(2)若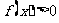 在
在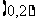 上恒成立,且函数
上恒成立,且函数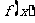 的最大值大于
的最大值大于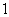 ,求实数
,求实数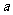 的取值范围,并由此猜测
的取值范围,并由此猜测 的单调性(无需证明);
的单调性(无需证明);
(3)对满足(2)的条件的一个常数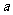 ,设
,设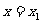 时,
时,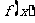 取得最大值。试构造一个定义在
取得最大值。试构造一个定义在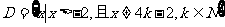 上的函数
上的函数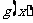 ,使当
,使当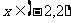 时,
时,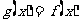 ,当
,当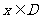 时,
时,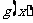 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以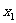 为首项的等差数列。
为首项的等差数列。
(文)已知函数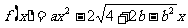 ,
,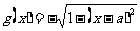 ,
,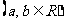
(Ⅰ)当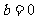 时,若
时,若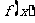 在
在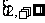 上单调递增,求
上单调递增,求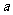 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对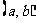 :当
:当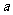 是整数时,存在
是整数时,存在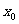 ,使得
,使得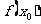 是
是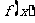 的最大值,
的最大值,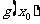 是
是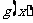 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对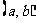 ,试构造一个定义在
,试构造一个定义在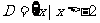 ,且
,且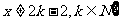 上的函数
上的函数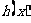 ,使当
,使当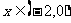 时,
时,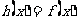 ,当
,当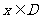 时,
时,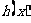 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以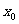 为首项的等差数列。
为首项的等差数列。
(理)解:(1)若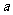 、
、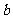 、
、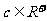 ,则
,则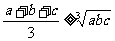 (当且仅当
(当且仅当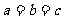 时取等号)。
时取等号)。
(2)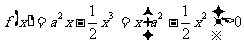 在
在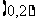 上恒成立,即
上恒成立,即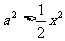 在
在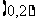 上恒成立,
上恒成立,
∵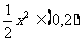 ,∴
,∴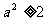 ,即
,即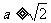 ,
,
又∵
 ∴
∴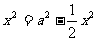 ,即
,即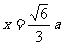 时,
时,
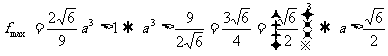 ,
,
又∵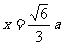
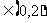 ,∴
,∴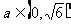 。
综上,得
。
综上,得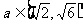 。
。
易知,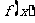 是奇函数,∵
是奇函数,∵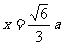 时,函数有最大值,
时,函数有最大值,
∴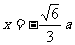 时,函数有最小值。
时,函数有最小值。
故猜测: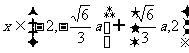 时,
时,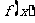 单调递减;
单调递减;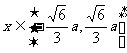 时,
时,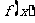 单调递增。
单调递增。
(3)依题意,只需构造以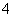 为周期的周期函数即可。
为周期的周期函数即可。
如对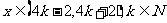 ,
,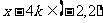 ,此时
,此时
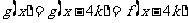 ,
,
即 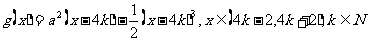 。
。
(文)解:(Ⅰ)当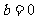 时,
时,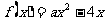 ,
,
若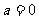 ,
,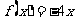 ,则
,则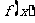 在
在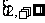 上单调递减,不符题意。
上单调递减,不符题意。
故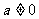 ,要使
,要使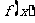 在
在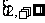 上单调递增,必须满足
上单调递增,必须满足 ,∴
,∴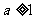 。
。
(Ⅱ)若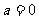 ,
,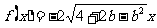 ,则
,则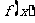 无最大值,故
无最大值,故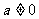 ,
,
∴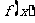 为二次函数,
为二次函数,
要使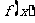 有最大值,必须满足
有最大值,必须满足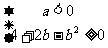 ,即
,即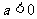 且
且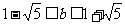 ,
,
此时,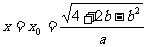 时,
时,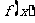 有最大值。
有最大值。
又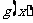 取最小值时,
取最小值时,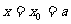 ,依题意,有
,依题意,有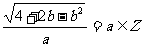 ,则
,则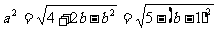 ,
,
∵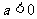 且
且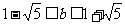 ,∴
,∴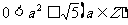 ,得
,得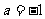 ,此时
,此时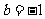 或
或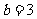 。
。
∴满足条件的实数对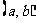 是
是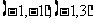 。
。
(Ⅲ)当实数对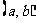 是
是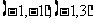 时,
时,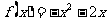
依题意,只需构造以2(或2的正整数倍)为周期的周期函数即可。
如对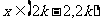 ,
,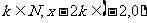 ,
,
此时, ,
,
故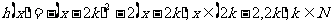

3、(12′=9′+3′)(理)设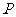 表示幂函数
表示幂函数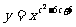 在
在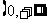 上是增函数的
上是增函数的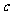 的集合;
的集合;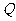 表示不等式
表示不等式 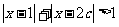 对任意
对任意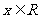 恒成立的
恒成立的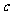 的集合。(1)求
的集合。(1)求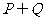 ;(2)试写出一个解集为
;(2)试写出一个解集为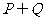 的不等式。
的不等式。
(文)设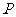 表示幂函数
表示幂函数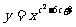 在
在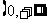 上是增函数的
上是增函数的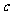 的集合;
的集合;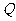 表示不等式
表示不等式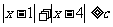 对任意
对任意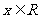 恒成立的
恒成立的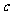 的集合。(1)求
的集合。(1)求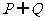 ;(2)试写出一个解集为
;(2)试写出一个解集为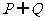 的不等式。
的不等式。
解:(理)(1)∵幂函数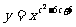 在
在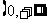 上是增函数,∴
上是增函数,∴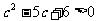 ,即
,即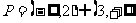 ,
,
又不等式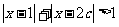 对任意
对任意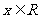 恒成立,∴
恒成立,∴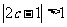 ,即
,即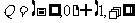 ,
,
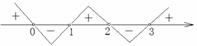 ∴
∴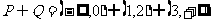 。
。
(2)一个解集为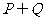 的不等式可以是
的不等式可以是
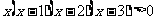 。
。
(文)(1)∵幂函数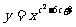 在
在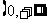 上是增函数,∴
上是增函数,∴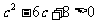 ,即
,即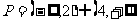 ,
,
又不等式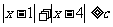 对任意
对任意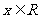 恒成立,∴
恒成立,∴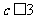 ,即
,即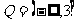 ,
,
∴ 。
。
(2)一个解集为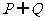 的不等式可以是
的不等式可以是
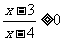 。
。
2、用水清洗一堆蔬菜上残留的农药的效果假定如下:用x单位量的水清洗一次以后,蔬菜上残留的农药量与这次清洗前残留的农药量之比为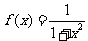 .
.
(Ⅰ)试解释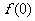 的实际意义;
的实际意义;
(Ⅱ)现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次.哪种方案清洗后蔬菜上残留的农药比较少?请说明理由.
解:(I)f(0)=1.表示没有用水清洗时,蔬菜上的农药量没有变化.……………2'
(Ⅱ)设清洗前蔬菜上的农药量为1,那么用a单位量的水清洗1次后.残留的农药量为 W1=1×f(a)=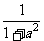 ;……………………………………………………………………4'
;……………………………………………………………………4'
又如果用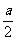 单位量的水清洗1次,残留的农药量为1×f(
单位量的水清洗1次,残留的农药量为1×f(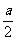 )=
)=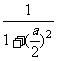 ,
,
此后再用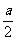 单位量的水清洗1次后,残留的农药量为
单位量的水清洗1次后,残留的农药量为
W2=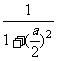 ·f(
·f(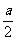 )=[
)=[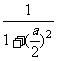 ]2=
]2=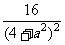 .……………………………8'
.……………………………8'
由于W1-W2=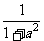 -
-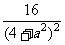 =
=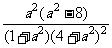 ,………………………9'
,………………………9'
故当a>2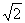 时,W1>W2,此时,把a单位量的水平均分成2份后,清洗两次,残留的农药量较少;当a=2
时,W1>W2,此时,把a单位量的水平均分成2份后,清洗两次,残留的农药量较少;当a=2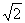 时,W1=W2,此时,两种清洗方式效果相同;当a<2
时,W1=W2,此时,两种清洗方式效果相同;当a<2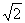 时,W1<W2,此时,把a单位量的水清洗一次,残留的农药量较少.…………………………12'
时,W1<W2,此时,把a单位量的水清洗一次,残留的农药量较少.…………………………12'
22.(本小题满分14分)
已知函数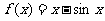
(Ⅰ)若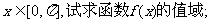
(Ⅱ)若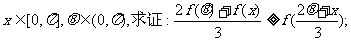
(Ⅲ)若
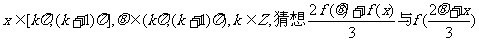 的大小关系(不必写出比较过程).
的大小关系(不必写出比较过程).
解:(Ⅰ)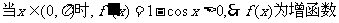

(Ⅱ)设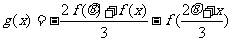
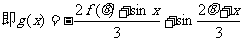
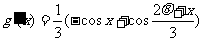 ……6分
……6分
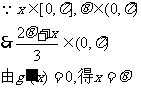
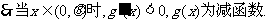
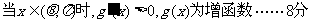

(Ⅲ)在题设条件下,当k为偶数时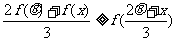
当k为奇数时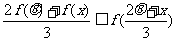 ……14分
……14分

21.(本小题满分12分)
垂直于x轴的直线交双曲线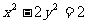 于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)
于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)
(Ⅰ)证明: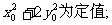
(Ⅱ)过P作斜率为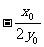 的直线l,原点到直线l的距离为d,求d的最小值.
的直线l,原点到直线l的距离为d,求d的最小值.
解(Ⅰ)证明: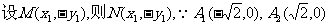
 ①
①
直线A2N的方程为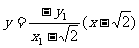 ②……4分
②……4分
①×②,得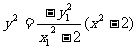

(Ⅱ)
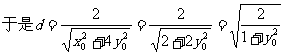 ……10分
……10分
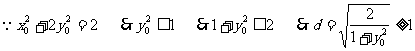
当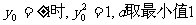 ……12分
……12分
3.唐山二模
22.(本小题满分14分)
(理)给定正整数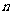 和正数
和正数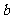 ,对于满足条件
,对于满足条件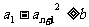 的所有无穷等差数列
的所有无穷等差数列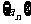 ,试求
,试求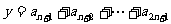 的最大值,并求出
的最大值,并求出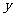 取最大值时
取最大值时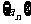 的首项和公差.
的首项和公差.
(文)给定正整数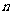 和正数
和正数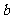 ,对于满足条件
,对于满足条件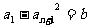 的所有无穷等差数列
的所有无穷等差数列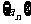 ,试求
,试求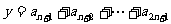 的最大值,并求出
的最大值,并求出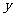 取最大值时
取最大值时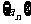 的首项和公差.
的首项和公差.
(理)解:设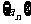 公差为
公差为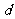 ,则
,则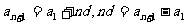 . 3分
. 3分
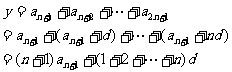
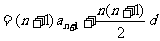 4分
4分
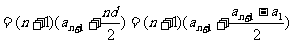
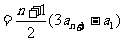 . 7分
. 7分
又 .
.
∴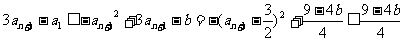 ,
,
当且仅当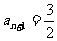 时,等号成立. 11分
时,等号成立. 11分
∴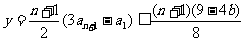 . 13分
. 13分
当数列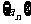 首项
首项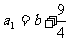 ,公差
,公差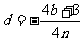 时,
时,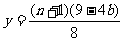 ,
,
∴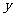 的最大值为
的最大值为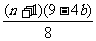 . 14分
. 14分
(文)解:设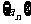 公差为
公差为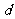 ,则
,则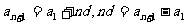 . 3分
. 3分
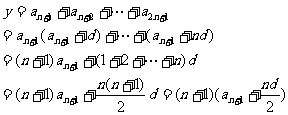
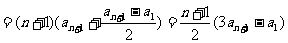 , 6分
, 6分
又 .
.
∴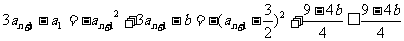 .
.
当且仅当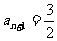 时,等号成立. 11分
时,等号成立. 11分
∴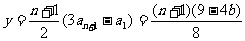 . 13分
. 13分
当数列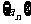 首项
首项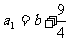 ,公差
,公差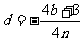 时,
时,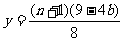 .
.
∴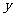 的最大值为
的最大值为 . 14分
. 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com