
21.(本小题满分12分)
设椭圆 的左焦点为
的左焦点为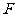 ,上顶点为
,上顶点为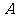 ,过点
,过点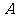 与
与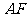 垂直的直线分别交椭圆和
垂直的直线分别交椭圆和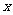 轴正半轴于
轴正半轴于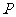 ,
,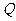 两点,且
两点,且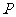 分向量
分向量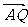 所成的比为8∶5.
所成的比为8∶5.
(1)求椭圆的离心率;
(2)若过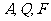 三点的圆恰好与直线
三点的圆恰好与直线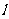 :
: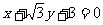 相切,求椭圆方程.
相切,求椭圆方程.
解:(1)设点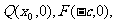 其中
其中 .
.
由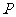 分
分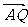 所成的比为8∶5,得
所成的比为8∶5,得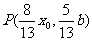 , 2分
, 2分
∴ .①, 4分
.①, 4分
而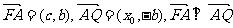 ,
,
∴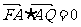 .
. .②, 5分
.②, 5分
由①②知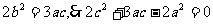 .
.
∴ . 6分
. 6分
(2)满足条件的圆心为 ,
,
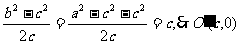 , 8分
, 8分
圆半径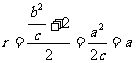 . 10分
. 10分
由圆与直线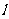 :
: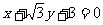 相切得,
相切得, ,
,
又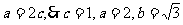 .
.
∴椭圆方程为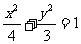 . 12分
. 12分
2.石家庄模拟
20. (本小题满分13分)
已知数列的前n项和为,且对任意自然数都成立,其中m为常数,且。
(I)求证数列是等比数列;
(II)设数列的公比,数列满足:
,试问当m为何值时,
成立?
解:(I)由已知
(2)
由得:,即对任意都成立
(II)当时,
由题意知
13分
19. (本小题满分14分)
设双曲线的两个焦点分别为,离心率为2。
(I)求此双曲线的渐近线的方程;
 (II)若A、B分别为上的点,且,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
(II)若A、B分别为上的点,且,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
(III)过点能否作出直线,使与双曲线交于P、Q两点,且。若存在,求出直线的方程;若不存在,说明理由。
解:(I)
,渐近线方程为 4分
(II)设,AB的中点
则M的轨迹是中心在原点,焦点在x轴上,长轴长为,短轴长为的椭圆。(9分)
(III)假设存在满足条件的直线
设
由(i)(ii)得
∴k不存在,即不存在满足条件的直线。 14分
1.北京丰台区二模
22. (14分)△ABC中,|AB|=|AC|=1,,P1为AB边上的一点,,从P1向BC作垂线,垂足是Q1;从Q1向CA作垂线,垂足是R1;从R1向AB作垂线,垂足是P2,再由P2开始重复上述作法,依次得Q2,R2,P3;Q3,R3,P4……
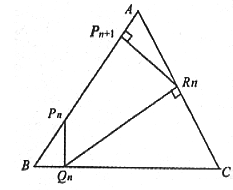
(1)令BPn为xn,寻求BPn与(即)之间的关系。
(2)点列是否一定趋向于某一个定点P0?说明理由;
(3)若,则是否存在正整数m,使点P0与Pm之间的距离小于0.001?若存在,求m的最小值。
解:(1)由|AB|=|AC|=1,
从而△ABC为边长为1的正三角形 2分
则,于是
∴ 3分
同样
4分
又
即 5分
(2)由(1)可得:
∴的等比数列
∴ 7分
当
∴点Pn趋向点P0,其中P0在AB上,且BP0 9分
(3) 11分
由
当
∴的最小值为4 14分

21. (12分)已知定点A(0,1),B(0,-1),C(1,0),动点P满足
(1)求动点P的轨迹方程,并说明方程表示的曲线。
(2)当
解:(1)设p(x,y)
则
由得
3分
整理得(*) 4分
当k=1时,*式化为x=1表示直线 5分
当k≠1时,*式化为
表示心为半径的圆 6分
(2)当k=2时,*式化为
此时,
∴其最小值为2,最大值为6 12分
3.德州模拟
21.(本小题满分12分)
已知函数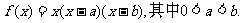
(Ⅰ)设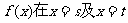 处取到极值,其中
处取到极值,其中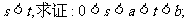
(Ⅱ)设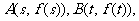 求证:线段AB的中点C在曲线y=f(x)上;
求证:线段AB的中点C在曲线y=f(x)上;
(Ⅲ)若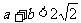 ,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直.
,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直.
解:(Ⅰ)以线段AB的中点O为原点,直线AB为x轴建立直角坐标系,
作CD⊥AB于D, 由题知: ①
①
而 ②
②
由①②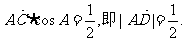 ………………2分
………………2分
同理,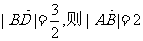 ∴A(-1,0)、B(1,0)……4分
∴A(-1,0)、B(1,0)……4分
设双曲线方程
由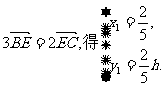 …………6分
…………6分
因为E、C两点在双曲线上,所以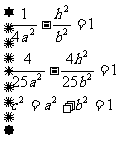 ………………8分
………………8分
解得 ,∴双曲线方程为
,∴双曲线方程为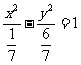 …………10分
…………10分
(Ⅱ)设
∵
∴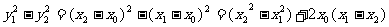 ①
①
又M、N在双曲线上,满足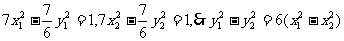 ②
②
将②代入①,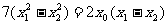
∵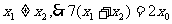 …………………………12分
…………………………12分
又
∴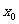 取值范围为(
取值范围为(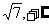 ) ………………14分
) ………………14分
20.(本小题满分12分)
数列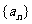 ,设Sn是数列的前n项和,并且满足
,设Sn是数列的前n项和,并且满足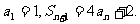
(Ⅰ)令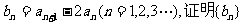 是等比数列,并求{bn}的通项公式;
是等比数列,并求{bn}的通项公式;
(Ⅱ)令
解:(Ⅰ)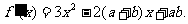
依题意知,s、t是二次方程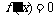 的两个实根.
的两个实根.
∵ ……2分
……2分
∴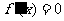 在区间(0,a)与(a,b)内分别有一个实根.
在区间(0,a)与(a,b)内分别有一个实根.
∵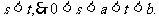 …………4分
…………4分
(Ⅱ)由s、t是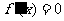 的两个实根,知
的两个实根,知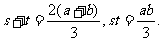
∴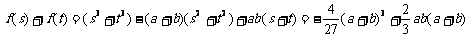 …6分
…6分
∵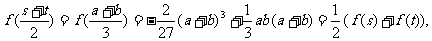
故AB的中点C(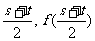 )在曲线y=f(x)上. ……8分
)在曲线y=f(x)上. ……8分
(Ⅲ)过曲线上点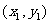 的切线方程为
的切线方程为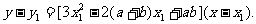
∵ ,又切线过原点.
,又切线过原点.
∴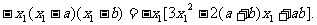
解得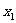 =0,或
=0,或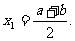
当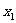 =0时,切线的斜率为ab;当
=0时,切线的斜率为ab;当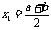 时,切线的斜率为
时,切线的斜率为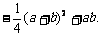 ……10分
……10分
∵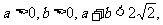 ∴两斜率之积
∴两斜率之积
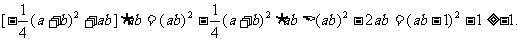
故两切线不垂直. ………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com