
 1测角仪原理
1测角仪原理
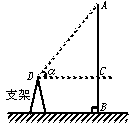
如图,对于建筑物AB,需测出角α,其中D为测角仪所处位置,在建筑物与地面垂直前提下,DC与地面平行DA为测角仪与建筑物顶端连线
2提出问题
(1)DC的水平如何保持?
(2)角α如何获得?
根据上述原理及所提问题,大家进行分组讨论,十五分钟后各组选一代表表述本组方案
3简易测角仪方案
方案Ⅰ
(1)实验器材:木板一块、量角器一个、三角架1个,硬纸条(3O cm), 铅垂线
铅垂线
(2)如图所示
①木板 ②硬纸条 ③支架 ④铅垂线 ⑤量角器 ⑥转动点
其中硬纸条、量角器固定在木板上,但可绕转动点⑥转动,木板固定在支架上,使铅垂线与矩形木板中心线重合以保持木板的水平
(3)测量时,使B、C和建筑物顶端重合,即三点一线,由于量角器随其移动,所以A点所示度数即所侧仰角的度数
(4)注意事项
①尽量加长BC以减少误差,②水平调整尤为重要,③测量多次数据取平均值,④测量时所选地面应保持水平
(5)不足之处
测量角度只能精确到1°
方案Ⅱ
 (1)实验器材:两个凳子、圆规、重垂线、三角板、卷尺
(1)实验器材:两个凳子、圆规、重垂线、三角板、卷尺
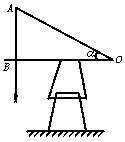
(2)示意图:
(3)测量步骤
①圆规一边OB固定在板凳边缘,
②在圆规另一边OA末端A点挂上重垂线,
③用三角板验证重垂线与OB是否垂直,若不垂直,可提升或降低O点,使它们垂直,
④用卷尺量出OB、AB长度,其中OA要与建筑物顶端共线,
⑤tanα=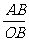 ,∴α=arctan
,∴α=arctan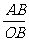
(4)注意事项
①圆规可用三合板,薄金属片之类材料做成,以减少测量误差,②在板凳上采取固定设施,可用钉子钉在板凳上,以防止测量时圆规的错位移动,③尽量使视线与O、A及所测建筑物的顶端位于同一直线上,④运算结果利用计算器得出
4研究问题
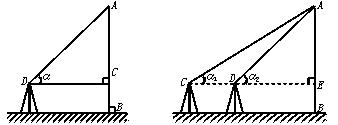 (1)测量底部能到达的建筑物高度
(1)测量底部能到达的建筑物高度
测出角α、DC长度,BC长度,在Rt△ADC中,求出AC,则AC+BC即为所求
(2)测量底部不能到达的建筑物高度
选点C、D两次测得仰角α1,α2,测出CD长度、BE长度
在△ACD中,利用正弦定理求出AD,而后在Rt△ADE中,求出AE,则AE+BE即为所求
4实习作业注意事项
(1)准备所需工具;(2)提前设计实习报告;(3)减少误差的措施;
(4)提前勘察地形以确定研究类型
5布置下节实习内容
测量电视发射塔的高度
前面两节,学习了解斜三角形的应用举例,具备了一定的解斜三角形的能力,并且了解到解斜三角形知识在生产、生活实际的各个方面的应用
这一节,我们将为应用解斜三角形知识的实习作业作准备工作
17.(2007北京四中模拟一)在△ABC中,A点的坐标为(3,0),BC边长为2,且BC在y轴上的区间[-3,3]上滑动.
(1)求△ABC外心的轨迹方程;
(2)设直线l∶y=3x+b与(1)的轨迹交于E,F两点,原点到直线l的距离为d,求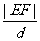 的最大值.并求出此时b的值.
的最大值.并求出此时b的值.
解 (1)设B点的坐标为(0,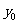 ),则C点坐标为(0,
),则C点坐标为(0,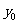 +2)(-3≤
+2)(-3≤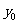 ≤1),
≤1),
则BC边的垂直平分线为y=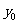 +1 ①
+1 ①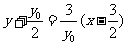 ②由①②消去
②由①②消去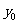 ,得
,得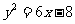 .∵
.∵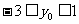 ,∴
,∴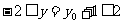 .故所求的△ABC外心的轨迹方程为:
.故所求的△ABC外心的轨迹方程为: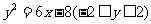 .
.
(2)将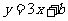 代入
代入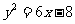 得
得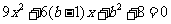 .由
.由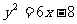 及
及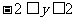 ,得
,得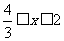 .所以方程①在区间
.所以方程①在区间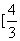 ,2
,2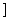 有两个实根.设
有两个实根.设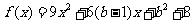 ,则方程③在
,则方程③在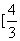 ,2
,2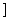 上有两个不等实根的充要条件是:
上有两个不等实根的充要条件是:
 得
得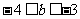
∵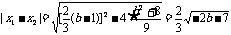 ∴
∴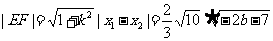
又原点到直线l的距离为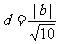 ,
,
∴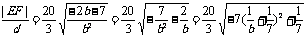 ∵
∵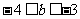 ,∴
,∴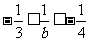 .
.
∴当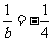 ,即
,即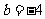 时,
时,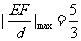 .
.
16. (江苏省泰兴市2007-2008学年第一学期高三调研)已知过点A(0,1),且方向向量为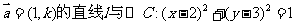 ,相交于M、N两点.
,相交于M、N两点.
(1)求实数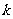 的取值范围;
的取值范围;
(2)求证: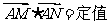 ;
;
(3)若O为坐标原点,且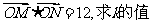 .
.
解 (1)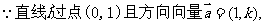

由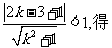
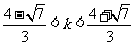 .
.
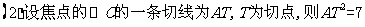
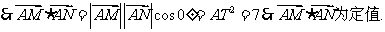
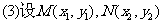
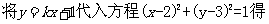
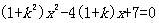
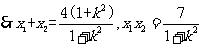
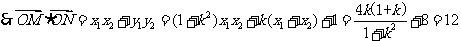
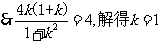
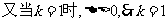 .
.
15.(广东地区2008年01月期末试题) 已知点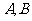 的坐标分别是
的坐标分别是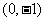 ,
,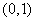 ,直线
,直线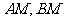 相交于点M,且它们的斜率之积为
相交于点M,且它们的斜率之积为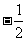 .
.
(1)求点M轨迹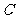 的方程;
的方程;
(2)若过点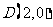 的直线
的直线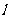 与(1)中的轨迹
与(1)中的轨迹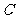 交于不同的两点
交于不同的两点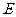 、
、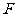 (
(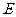 在
在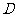 、
、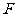 之间),试求
之间),试求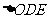 与
与 面积之比的取值范围(
面积之比的取值范围(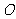 为坐标原点).
为坐标原点).
解(1)设点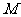 的坐标为
的坐标为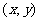 ,
,
∵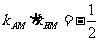 ,∴
,∴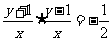 .
.
整理,得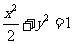 (
(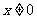 ),这就是动点M的轨迹方程.
),这就是动点M的轨迹方程.
(2)方法一 由题意知直线 的斜率存在,
的斜率存在,
设 的方程为
的方程为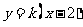 (
(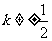 )
①
)
①
将①代入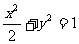 ,
,
得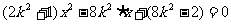 ,
,
由 ,解得
,解得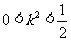 .
.
设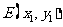 ,
,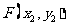 ,则
,则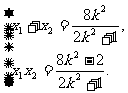 ②
②
令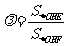 ,则
,则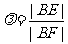 ,即
,即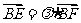 ,即
,即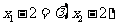 ,且
,且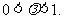
由②得,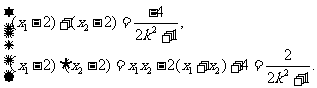
即
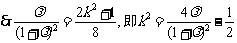 .
.
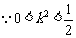 且
且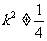
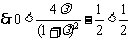 且
且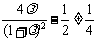 .
.
解得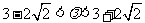 且
且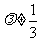
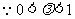 ,
,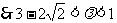 且
且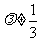 .
.
∴△OBE与△OBF面积之比的取值范围是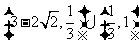 .
.
方法二 由题意知直线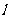 的斜率存在,
的斜率存在,
设 的方程为
的方程为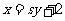
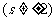 ①
①
将①代入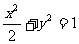 ,
,
整理,得 ,
,
由 ,解得
,解得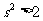 .
.
设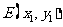 ,
,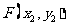 ,则
,则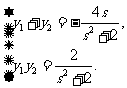 ②
②
令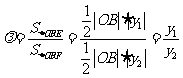 ,且
,且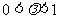 .
.
将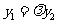 代入②,得
代入②,得
∴ .即
.即 .
.
∵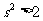 且
且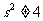 ,∴
,∴ 且
且 .
.
即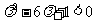 且
且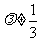 .
.
解得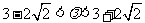 且
且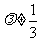 .
.
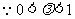 ,
,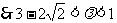 且
且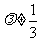 .
.
故△OBE与△OBF面积之比的取值范围是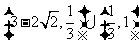 .
.
14.(江苏省南京市2008届高三第一次调研测试)已知:以点C (t, )(t∈R , t ≠ 0)为圆心的圆与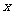 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程.
解 (1)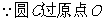 ,
,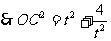 .
.
设圆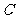 的方程是
的方程是 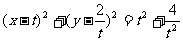
令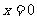 ,得
,得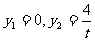 ;令
;令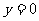 ,得
,得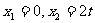
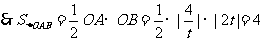 ,即:
,即: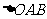 的面积为定值.
的面积为定值.
(2)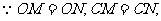
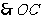 垂直平分线段
垂直平分线段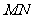 .
.
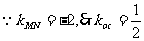 ,
,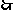 直线
直线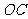 的方程是
的方程是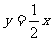 .
.
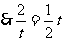 ,解得:
,解得: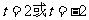
当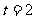 时,圆心
时,圆心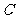 的坐标为
的坐标为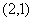 ,
,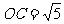 ,
,
此时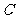 到直线
到直线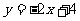 的距离
的距离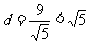 ,
,
圆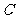 与直线
与直线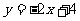 相交于两点.
相交于两点.
当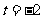 时,圆心
时,圆心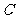 的坐标为
的坐标为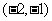 ,
,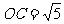 ,
,
此时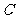 到直线
到直线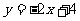 的距离
的距离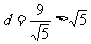
圆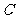 与直线
与直线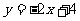 不相交,
不相交,
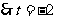 不符合题意舍去.
不符合题意舍去.
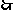 圆
圆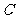 的方程为
的方程为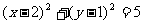 .
.
13.(唐山二模)⊙M:x2+y2=4,点P(x0,y0)在圆外,则直线x0x+y0y=4与⊙M的位置关系是_____
答案 相交
12.(2007石家庄一模)若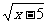 ≠kx+2对一切x≥5都成立,则k的取值范围是________.
≠kx+2对一切x≥5都成立,则k的取值范围是________.
答案 k>1/10或k<2/5
11. (江苏省泰兴市2007-2008学年第一学期高三调研)设直线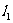 的方程为
的方程为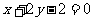 ,
,
将直线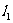 绕原点按逆时针方向旋转
绕原点按逆时针方向旋转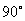 得到直线
得到直线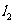 ,则
,则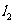 的方程是
的方程是
答案 2x-y+2=0
10.(湖南省长沙市一中2008届高三第六次月考)设直线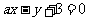 与圆(x-1)2+(y-2)2=4
与圆(x-1)2+(y-2)2=4
相交于A、B两点,且弦长为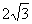 ,则a=
。
,则a=
。
答案 0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com