
10. 解:(1)由题意知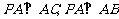 ,则
,则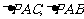 均为直角三角形…………………1分
均为直角三角形…………………1分
在 中,
中,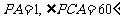 ,解得
,解得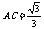 …………………………2分
…………………………2分
在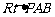 中,
中,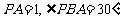 ,解得
,解得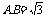 …………………………3分
…………………………3分
又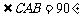 ,
,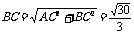 万米. …………………………5分
万米. …………………………5分
(2)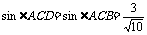 ,
,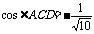 ,…………………………7分
,…………………………7分
又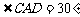 ,所以
,所以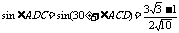 .…………………………9分
.…………………………9分
在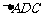 中,由正弦定理,
中,由正弦定理,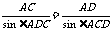 …………………………10分
…………………………10分
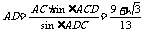 万米…………………………12分
万米…………………………12分
9. 根据余弦定理 AB2=a2+b2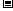 2abcos
2abcos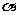 , AB=
, AB= .……………4分
.……………4分
cosB=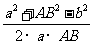 =
=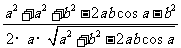
=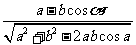 ,从而确定
,从而确定 B的大小. ……………8分
B的大小. ……………8分
同理可以得到cosA=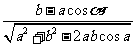 ,从而确定
,从而确定 A的大小. …………12分
A的大小. …………12分
8. (1)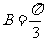 ,(2)
,(2)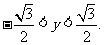
7. 由题意知: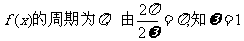 。------------3分
。------------3分
由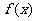 最大值为2,故
最大值为2,故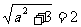 ,又
,又 ,
,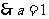 ------------6分
------------6分
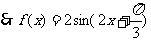 ……………………………………… 7分
……………………………………… 7分
(II)由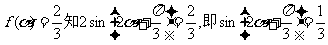 。
。
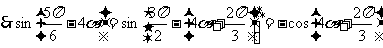
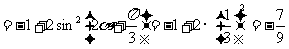 。………………………12分
。………………………12分
6. 解:(Ⅰ)(方法一)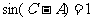 ,又
,又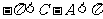 ,
,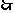
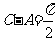 , ……..1分
, ……..1分
又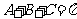 ,∴
,∴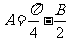 ,
……………………..2分
,
……………………..2分
∴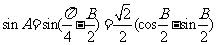 ,
……………………..4分
,
……………………..4分
∴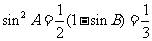 ,又
,又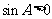 ,∴
,∴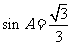 . ……………………6分
. ……………………6分
(方法二)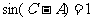 ,又
,又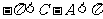 ,
,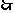
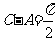 , ………1分
, ………1分
又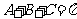 ,∴
,∴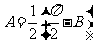 ,
……………………..2分
,
……………………..2分
∴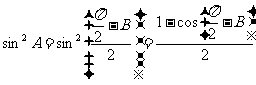 ,
……………………..4分
,
……………………..4分
∴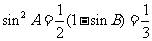 ,又
,又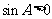 ,∴
,∴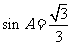 . ……………………6分
. ……………………6分
又(方法三)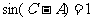 ,又
,又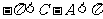 ,
,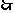
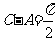 , ……..1分
, ……..1分
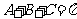 ,∴B=
,∴B=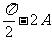 ,
……………………2分
,
……………………2分
∵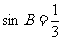 ∴
∴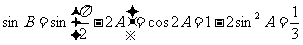 ,
,
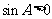 ,∴
,∴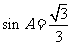 . ……………………6分
. ……………………6分
(Ⅱ)由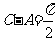 易知
易知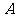 、
、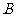 都是锐角,
都是锐角,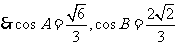 ,
,
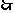
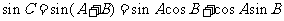
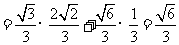 ,…8分
,…8分
由正弦定理可知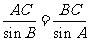 ∴
∴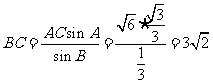 , ……10分
, ……10分
∴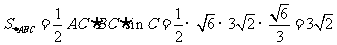 . ……………….12分
. ……………….12分
5. ⑴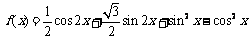
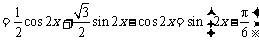 ,
,
∴最小正周期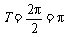 .
.
由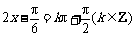 ,得
,得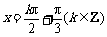
函数图象的对称轴方程为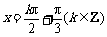
⑵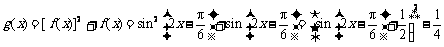
当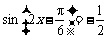 时,
时,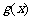 取得最小值
取得最小值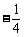 ;
;
当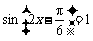 时,
时,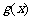 取得最大值2,
取得最大值2,
所以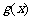 的值域为
的值域为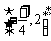 .
.
4. 解答:(1)当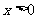 时,
时,
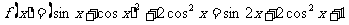

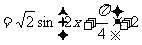
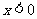 时,
时,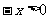 ,
,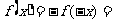
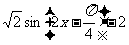 (6分)
(6分)
(2)若关于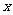 的方程
的方程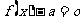 有解,
有解,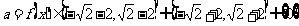 (12分)
(12分)
3. 解:(Ⅰ)在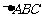 中,由
中,由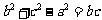 及余弦定理得
及余弦定理得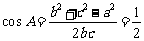 …2分
…2分
而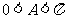 ,则
,则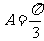 ; …………………4分
; …………………4分
(Ⅱ)由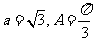 及正弦定理得
及正弦定理得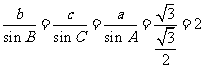 ,…………6分
,…………6分
同理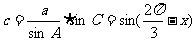 …………………8分
…………………8分
∴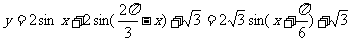 ……………………10分
……………………10分
∵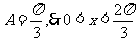 ∴
∴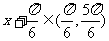 ,
,
∴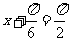 即
即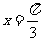 时,
时,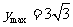 。 …………………12分
。 …………………12分
2. 解:10分钟后由观察点P测得气球在P的正东方向,仰角为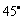 的S点处,
的S点处,
即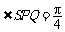 ,
所以
,
所以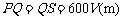 . (2分),
. (2分),
又10分钟后测得气球在P的东偏北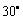 ,其仰角为
,其仰角为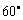 的T点处,
的T点处,
即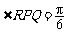 ,
,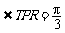 ,RT=2QS=1200V(m),(4分),
,RT=2QS=1200V(m),(4分),
于是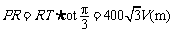 . (5分),在
. (5分),在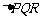 中由余弦定理得:
中由余弦定理得:
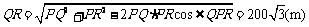 .(7分),
.(7分),
因为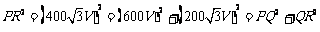 ,所以
,所以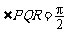 ,
,
即风向为正南风. (8分),
因为气球从S点到T点经历10分钟,即600s,
所以风速为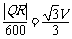 (m/s). (9分)
(m/s). (9分)
答:风向为正南风,风速为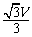 m/s. (10分)
m/s. (10分)
1. ⑴因为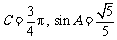
所以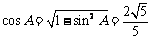
由已知得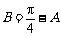 .
.
所以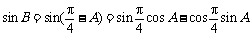
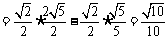
⑵由⑴知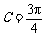 .
所以
.
所以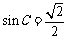 且
且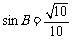 .
.
由正弦定理得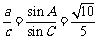 .
.
又因为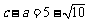 ,所以
,所以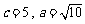 .
.
所以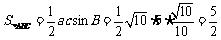
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com