
4. =(2,3),
=(2,3), =(-2,4),则(
=(-2,4),则( +
+ )·(
)·( -
- )= .
)= .
3.已知 =(4,3),向量
=(4,3),向量 是垂直
是垂直 的单位向量,则
的单位向量,则 等于( )
等于( )
A. 或
或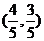 ?
B.
?
B. 或
或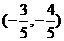 ?
?
?C.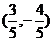 或
或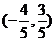 ? D.
? D.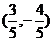 或
或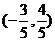 ?
?
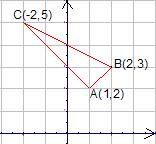
2.已知 (1,2),
(1,2), (2,3),
(2,3),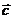 (-2,5),则△
(-2,5),则△

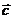 为( )
为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不等边三角形
1.若 =(-4,3),
=(-4,3), =(5,6),则3|
=(5,6),则3| |2-4
|2-4 =( )
=( )
A.23 ?B.57 ?C.63 ?D.83
例1 设 = (5, -7),
= (5, -7), = (-6, -4),求
= (-6, -4),求 ×
×
解: = 5×(-6) + (-7)×(-4) = -30 + 28 = -2
= 5×(-6) + (-7)×(-4) = -30 + 28 = -2
例2 已知 (1, 2),
(1, 2), (2, 3),
(2, 3),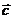 (-2, 5),求证:△ABC是直角三角形
(-2, 5),求证:△ABC是直角三角形
证明:∵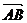 =(2-1, 3-2) = (1, 1),
=(2-1, 3-2) = (1, 1), 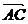 = (-2-1, 5-2) = (-3, 3)
= (-2-1, 5-2) = (-3, 3)
∴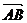 ×
×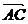 =1×(-3) + 1×3 = 0 ∴
=1×(-3) + 1×3 = 0 ∴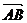 ^
^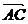
∴△ABC是直角三角形
例3
已知 = (3, -1),
= (3, -1), = (1, 2),求满足
= (1, 2),求满足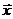 ×
× = 9与
= 9与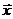 ×
× = -4的向量
= -4的向量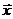
解:设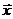 = (t, s),
= (t, s),
由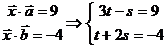
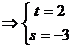 ∴
∴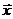 = (2, -3)
= (2, -3)
例4 已知 =(1,
=(1, ),
), =(
=( +1,
+1, -1),则
-1),则 与
与 的夹角是多少?
的夹角是多少?
分析:为求 与
与 夹角,需先求
夹角,需先求 及|
及| |·|
|·| |,再结合夹角θ的范围确定其值.
|,再结合夹角θ的范围确定其值.
解:由 =(1,
=(1, ),
), =(
=( +1,
+1, -1)
-1)
有 ·
· =
= +1+
+1+ (
( -1)=4,|
-1)=4,| |=2,|
|=2,| |=2
|=2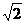 .
.
记 与
与 的夹角为θ,则cosθ=
的夹角为θ,则cosθ=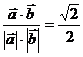
又∵0≤θ≤π,∴θ=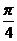
评述:已知三角形函数值求角时,应注重角的范围的确定.
例5
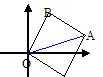
如图,以原点和A
(5, 2)为顶点作等腰直角△ABC,使Ð = 90°,求点
= 90°,求点 和向量
和向量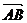 的坐标
的坐标
解:设 点坐标(x,
y),则
点坐标(x,
y),则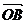 = (x, y),
= (x, y),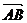 = (x-5, y-2)
= (x-5, y-2)
∵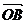 ^
^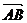 ∴x(x-5) + y(y-2) = 0即:x2 + y2
-5x - 2y = 0
∴x(x-5) + y(y-2) = 0即:x2 + y2
-5x - 2y = 0
又∵|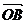 | = |
| = |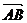 | ∴x2 + y2
= (x-5)2 + (y-2)2即:10x + 4y
= 29
| ∴x2 + y2
= (x-5)2 + (y-2)2即:10x + 4y
= 29
 由
由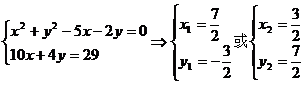
∴ 点坐标
点坐标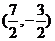 或
或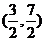 ;
;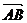 =
=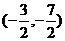 或
或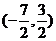
例6 在△ABC中,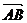 =(2, 3),
=(2, 3),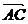 =(1, k),且△ABC的一个内角为直角,
=(1, k),且△ABC的一个内角为直角,
求k值
解:当 = 90°时,
= 90°时,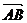 ×
×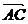 = 0,∴2×1 +3×k =
0 ∴k =
= 0,∴2×1 +3×k =
0 ∴k =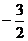
当 = 90°时,
= 90°时,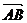 ×
×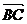 = 0,
= 0,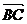 =
=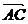 -
-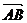 = (1-2, k-3) = (-1, k-3)
= (1-2, k-3) = (-1, k-3)
∴2×(-1) +3×(k-3) = 0 ∴k =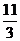
当C= 90°时,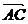 ×
×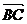 = 0,∴-1 + k(k-3) = 0 ∴k =
= 0,∴-1 + k(k-3) = 0 ∴k =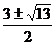
4.两向量夹角的余弦(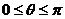 )
)
cosq =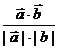

3.向量垂直的判定
设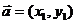 ,
,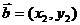 ,则
,则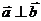
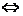
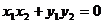
⒈平面两向量数量积的坐标表示
已知两个非零向量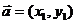 ,
,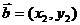 ,试用
,试用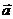 和
和 的坐标表示
的坐标表示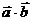
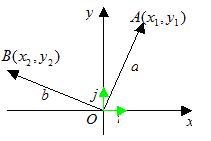
设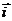 是
是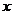 轴上的单位向量,
轴上的单位向量,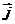 是
是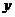 轴上的单位向量,那么
轴上的单位向量,那么
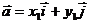 ,
,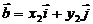
所以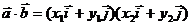
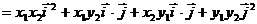
又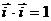 ,
,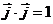 ,
,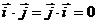
所以
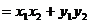
这就是说:两个向量的数量积等于它们对应坐标的乘积的和
即
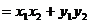
2.平面内两点间的距离公式
(1)设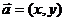 ,则
,则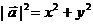 或
或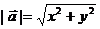
(2)如果表示向量 的有向线段的起点和终点的坐标分别为
的有向线段的起点和终点的坐标分别为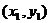 、
、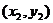 ,那么
,那么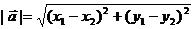 (平面内两点间的距离公式)
(平面内两点间的距离公式)
5. 平面向量数量积的运算律
交换律: ×
×  =
=  ×
× 
数乘结合律:(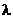
 )×
)× =
=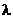 (
( ×
× ) =
) =  ×(
×(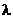
 )
)
分配律:( +
+  )×
)×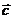 =
=  ×
×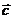 +
+  ×
×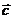
4.两个向量的数量积的性质:
设 、
、 为两个非零向量,
为两个非零向量,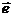 是与
是与 同向的单位向量
同向的单位向量
1°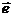 ×
× =
=  ×
×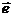 =|
=| |cosq;2°
|cosq;2° ^
^ Û
Û  ×
× = 0
= 0
3°当 与
与 同向时,
同向时, ×
× = |
= | ||
|| |;当
|;当 与
与 反向时,
反向时, ×
× = -|
= -| ||
|| |
|
特别的 ×
× = |
= | |2或
|2或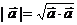
 4°cosq =
4°cosq =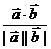 ;5°|
;5°| ×
× | ≤ |
| ≤ | ||
|| |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com