
(八)读右图。
 20.关于图中河湖补给关系的说法,正确的是 ( )
20.关于图中河湖补给关系的说法,正确的是 ( )
A.甲河补给A湖 B.A湖补给甲河
C.B湖补给乙河 D.乙河属于外流河
21.如果两幅图中等高距相同,下列说法正确
的是 ( )
A.甲河比乙河流速快
B.乙河比甲河流速快
C.甲河、乙河流速相同
 D.无法确定河流的流速
D.无法确定河流的流速
(七)在技术中,可以根据地物反射和辐射的渡谱特征来判断地物的状况。
17.阴雨天气中,对地物的分辨率较高的是 ( )
A.飞机可见光遥感 B.卫星可见光遥感
C.飞机微波遥感 D.卫星微波遥感
18.利用遥感技术,可以判断农作物的生长状况。这是因为 ( )
A.不同生长状况的农作物反射波谱不同
B.根据遥感图像可判断出土壤肥力的高低
|
D.根据遥感图像可判断出病虫害类型
19.在假彩色影像上,草、树和庄稼覆盖地区通常为 ( )
A.灰色和蓝色 B.灰白色 C.浅蓝色 D.红色
(三)2009年2月10日11点55分(西五区时间),美国“铱33”商业通信卫星和俄罗斯“宇宙2251”军用通信卫星在(72°N、98°E)高约790千米相撞,产生12000块碎片。
7.两卫星撞击点在大气层中的 ( )
A.对流层 B.平流层 C.中间层 D.电离层
8.两卫星撞击时北京时间为 ( )
A.2月11日0点55分 B.2月10日4点55分
C.2月9日22点55分 D.2月10日8点55分
9.两颗卫星相撞的时候,地球上太阳直射点的位置在 ( )
A.赤道和北回归线之间 B.北回归线和北极圈之间
C.赤道和南回归线之间 D.南回归线和南极圈之间
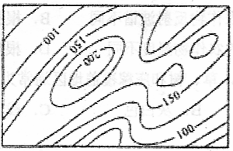 (四)地形等高线的弯曲与疏密蕴含着许多关于地形的信息。
(四)地形等高线的弯曲与疏密蕴含着许多关于地形的信息。
右图是某地区等高线地形示意图。
10.图中所示地区山脊的基本走向为( )
A.东北一西南向 B.东西向
C.西北一东南向 D.南北向
11.图示山体主峰的西北坡地形特征是( )
A.上、下部均陡峭
B.上部较陡,下部较缓
C.上、下部均平缓
D.上部较缓,下部较陡
 (五)右下图是某城市从市中心到远郊的土地利用空间结构示意图。
(五)右下图是某城市从市中心到远郊的土地利用空间结构示意图。
12.该城市2000年与2007年地价变化
反映了 ( )
①远郊地价升位幅度高于市中心
②地价整体有所上涨
③中心城区范围扩大
④城市规模扩大
A.①② B.①③
C.②④ D.③④
13.在2007年地价变化曲线上,近郊区地价出现了两个峰,根据城市功能分区理论模型推测该区可能建设了 ( )
①蔬菜种植基地 ②高新技术开发区 ③大学城 ④美术馆
A.①② B.②③ C.③④ D.①④
 (六)2009年2月25日,百岁外白渡桥重返苏州河。北跨桥身借助潮汐“回家”后第二
(六)2009年2月25日,百岁外白渡桥重返苏州河。北跨桥身借助潮汐“回家”后第二
天,南跨桥身也复位成功。
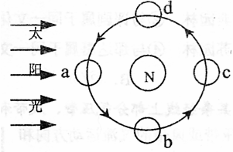
14.外白渡桥北跨拆身“回家”时,正值农历二月
初一。此时月球正处右侧“月球公转示意图”
中的 ( )
A.a B.b
C.c D.d
15.若仅考虑天文因素的影响,南跨桥身复位当日的涨潮时间比前一天约晚 ( )
A.25分钟 B.50分钟 C.15分钟 D.30分钟
16.外白渡桥东侧建造了苏州河河口水闸,其主要作用是 ( )
①防止船只碰撞、损毁外白渡桥 ②预防大潮汛,确保苏州河防汛墙安全
③调节苏州河水位,冲刷河道污染物 ④保证苏州河流量,提高通航能力
A.①② B.②③ C.②④ D.①④
(二)一些指标可以用来表示地理现象的发生与变化
4.下列叙述正确的是 ( )
A.老年人口比重≥7%为老龄化开始 B.震级≥7级始称为破坏生地震
C.中心风力超过12级为热带风暴 D.领海宽度为12千米
5.下列叙述正确的是 ( )
A.衡量人口分布的指标是人口总量
B.衡量水资源的指标是多年平均径流总量
C.衡量城市化水平的指标是居民人口总量
D.衡量对外贸易水平的指标是货运总量
6.决定气旋或反气旋天气系统内风速大小的直接原因是 ( )
A.地转偏向力 B.水平气压梯度力
C.下垫面摩擦力 D。气温递减率
 (一)板块构造学说是20世纪最重要的科学成果之一。右图为某种类型的板块边界示意图。
(一)板块构造学说是20世纪最重要的科学成果之一。右图为某种类型的板块边界示意图。
1.图示的板块边界是 ( )
A.人陆板块与大陆板块的碰撞边界
B.大洋板块内部的生蚝边界
C.大洋板块向大陆扳块的俯冲边界
D.大陆板块内部的生长边界
2.以下地貌单元中,成冈与图示机理相关的是 ( )
A.东非大裂谷 B.日本列岛 C.阿尔卑斯山脉 D.落基山脉
3.板块构造学说有助于人类进一步认识 ( )
①海陆问水循环的机理 ②洋流分布和运动规律
③地震分布和活动规律 ④矿产资源的分布规律
A.①② B.②③ C.③④ D.①③
10.(2006北京)已知点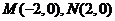 ,动点
,动点 满足条件
满足条件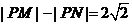 .记动点
.记动点 的轨迹为
的轨迹为 .
.
(Ⅰ)求 的方程;
的方程;
(Ⅱ)若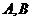 是
是 上的不同两点,
上的不同两点,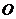 是坐标原点,求
是坐标原点,求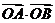 的最小值.
的最小值.
解法一:
(Ⅰ)由|PM|-|PN|=2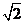 知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长a=
知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长a=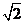 .
.
又半焦距c=2。故虚半轴长b= ,
,
所以W的方程为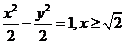
(Ⅱ)设A、B的坐标分别为(x1y1),(x2y2).
当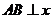 轴时,
轴时,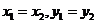 ,从而
,从而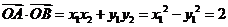 。
。
当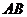 与
与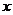 轴不垂直时,设直线
轴不垂直时,设直线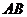 的方程为
的方程为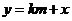 ,与
,与 的方程联立,消去
的方程联立,消去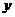 得
得
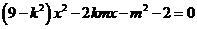 ,
,
故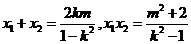
所以
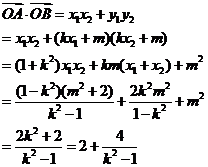
又因为 ,所以
,所以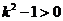 ,从而
,从而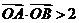 .
.
综上,当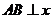 轴时,
轴时,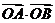 取得最小值2.
取得最小值2.
解法二:
(Ⅰ)同解法一.
(Ⅱ)设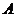 、
、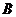 的坐标分别为
的坐标分别为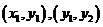 ,则
,则
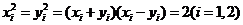
令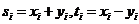 ,
,
则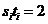 ,且
,且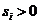 ,
,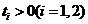 ,所以
,所以

当且仅当 ,即
,即 时“=”成立.
时“=”成立.
所以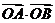 的最小值是2.
的最小值是2.
[探索题](2006安徽)如图,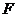 为双曲线
为双曲线 的右焦点,
的右焦点, 为双曲线
为双曲线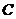 右支上一点,且位于
右支上一点,且位于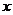 轴上方,
轴上方,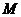 为左准线上一点,
为左准线上一点,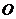 为坐标原点。已知四边形
为坐标原点。已知四边形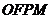 为平行四边形,
为平行四边形,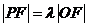 。
。
(Ⅰ)写出双曲线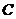 的离心率
的离心率 与
与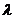 的关系式;
的关系式;
(Ⅱ)当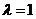 时,经过焦点
时,经过焦点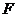 且平行于
且平行于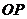 的直线交双曲线于
的直线交双曲线于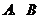 两点,若
两点,若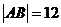 ,求此时的双曲线方程。
,求此时的双曲线方程。
(Ⅰ)解法1:设M′为PM与双曲线右准线的交点,F(c,0),则
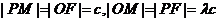


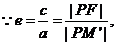

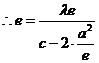
即
解法2:设 为
为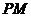 与双曲线右准线的交点,N为左准线与x轴的交点.
与双曲线右准线的交点,N为左准线与x轴的交点.
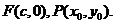 由于
由于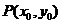 在双曲线右支上,则
在双曲线右支上,则
 ①
①
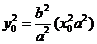 ②
②
由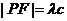 得
得
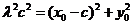 ③
③
将①、②代入③得
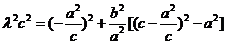
再将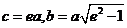 代入上式,得
代入上式,得
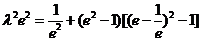
化简,得
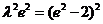 ④
④
由题意,点P位于双曲线右支上,从而
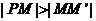
于是 即
即 又
又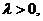 所以由④式得
所以由④式得

(Ⅱ)解:当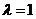 时,由
时,由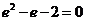 解得
解得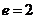
从而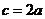 ,
,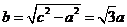
由此得双曲线得方程是

下面确定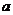 的值
的值
解法1:
设双曲线左准线与x轴的交点为N,P点的坐标为(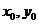 ),则
),则
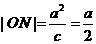 ,
,
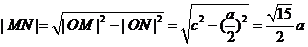
由于P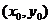 在双曲线的右支上,且位于x轴上方,因而
在双曲线的右支上,且位于x轴上方,因而
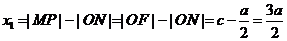 ,
,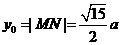
所以直线OP的斜率为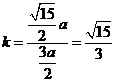
设过焦点F且平行于OP的直线与双曲线的交点为A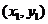 、B
、B ,则
,则
直线AB的斜线为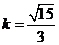 ,直线AB的方程为
,直线AB的方程为
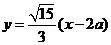
将其代入双曲线方程整理得

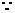
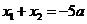 ,
,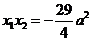
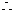
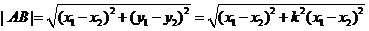
=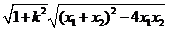
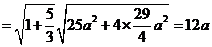
由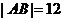 得
得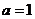 ,于是,所求双曲线得方程为
,于是,所求双曲线得方程为
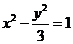
解法2.由条件知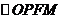 为菱形,其对角线OP与FM互相垂直平分,
为菱形,其对角线OP与FM互相垂直平分,
其交点Q为OP得中点
9.已知抛物线C:y2=4(x-1),椭圆C1的左焦点及左准线与抛物线C的焦点F和准线l分别重合.
(1)设B是椭圆C1短轴的一个端点,线段BF的中点为P,求点P的轨迹C2的方程;
(2)如果直线x+y=m与曲线C2相交于不同两点M、N,求m的取值范围.
(1)解法一:由y2=4(x-1)知抛物线C的焦点F坐标为(2,0).准线l的方程为x=0.设动椭圆C1的短轴的一个端点B的坐标为(x1,y1)(x1>2,y1≠0),点P(x,y),
|
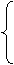
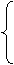
|
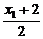 , x1=2x-2,
, x1=2x-2,
y=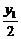 ,
y1=2y.
,
y1=2y.
∴B(2x-2,2y)(x>2,y≠0).
设点B在准线x=0上的射影为点B′,椭圆的中心为点O′,则椭圆离心率e=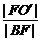 ,由
,由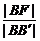 =
=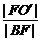 ,得
,得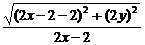 =
=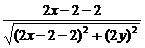 ,
,
整理,化简得y2=x-2(y≠0),这就是点P的轨迹方程.
解法二:抛物线y2=4(x-1)焦点为F(2,0),准线l:x=0.设P(x,y),
∵P为BF中点,
∴B(2x-2,2y)(x>2,y≠0).设椭圆C1的长半轴、短半轴、半焦距分别为a、b、c,
则c=(2x-2)-2=2x-4,b2=(2y)2=4y2,
∵(-c)-(- )=2,
)=2,
∴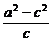 =2,
=2,
即b2=2c.∴4y2=2(2x-4),
即y2=x-2(y≠0),此即C2的轨迹方程.
|
|
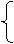 x+y=m,
x+y=m,
y2=x-2
m>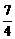 .
.
而当m=2时,直线x+y=2过点(2,0),这时它与曲线C2只有一个交点,
∴所求m的取值范围是(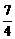 ,2)∪(2,+∞).
,2)∪(2,+∞).
8.(2006上海) 在平面直角坐标系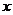 O
O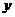 中,直线
中,直线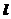 与抛物线
与抛物线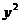 =2
=2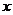 相交于A、B两点
相交于A、B两点
(1)求证:“如果直线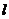 过点T(3,0),那么
过点T(3,0),那么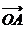
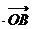 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由
[解](1)设过点T(3,0)的直线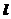 交抛物线y2=2x于点A(x1,y1)、B(x2,y2)
交抛物线y2=2x于点A(x1,y1)、B(x2,y2)
当直线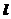 的钭率不存在时,直线
的钭率不存在时,直线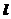 的方程为x=3,此时,直线
的方程为x=3,此时,直线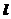 与抛物线相交于点A(3,
与抛物线相交于点A(3,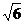 )、B(3,-
)、B(3,-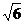 )
) ∴
∴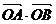 =3;
=3;
当直线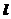 的钭率存在时,设直线
的钭率存在时,设直线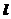 的方程为
的方程为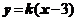 ,其中
,其中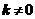 ,
,
由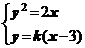 得
得 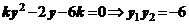
又 ∵
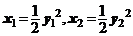 ,
,
∴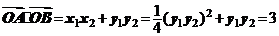 ,
,
综上所述,命题“如果直线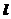 过点T(3,0),那么
过点T(3,0),那么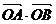 =3”是真命题;
=3”是真命题;
(2)逆命题是:设直线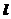 交抛物线y2=2x于A、B两点,如果
交抛物线y2=2x于A、B两点,如果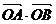 =3,那么该直线过点T(3,0)
=3,那么该直线过点T(3,0) 该命题是假命题
该命题是假命题
例如:取抛物线上的点A(2,2),B(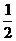 ,1),此时
,1),此时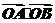 =3,
=3,
直线AB的方程为: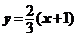 ,而T(3,0)不在直线AB上;
,而T(3,0)不在直线AB上;
说明:由抛物线y2=2x上的点A (x1,y1)、B (x2,y2) 满足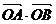 =3,可得y1y2=-6,
=3,可得y1y2=-6,
或y1y2=2,如果y1y2=-6,可证得直线AB过点(3,0);如果y1y2=2,可证得直线AB过点(-1,0),而不过点(3,0)
7. 正方形ABCD中,一条边AB在直线y=x+4上,另外两顶点C、D在抛物线y2=x上,求正方形的面积.
解:设CD所在直线的方程为y=x+t,
|
|
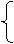 y=x+t,
y=x+t,
y2=x,
x2+(2t-1)x+t2=0,
∴|CD|=
=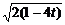 .
.
又直线AB与CD间距离为|AD|= ,
,
∵|AD|=|CD|,
∴t=-2或-6.
从而边长为3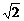 或5
或5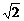 .
.
面积S1=(3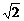 )2=18,S2=(5
)2=18,S2=(5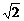 )2=50.
)2=50.
6.设过焦点F(1,0)的直线为y=k(x-1)(k≠0),A(x1,y1),B(x2,y2)
代入抛物线方程消去y得k2x2-2(k2+2)x+k2=0.
∵k2≠0,∴x1+x2=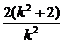 ,
,
|AB|=x1+x2+2=8, x1+x2=6. 可得k2=1.
∴△OAB的重心的横坐标为x=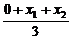 =2.
=2.
.法2: 由|AB|=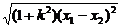 =8, 得k2=1…..
=8, 得k2=1…..
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com