
21.解:(1)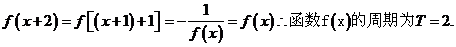
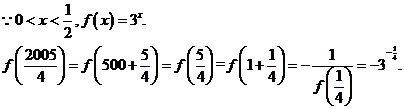
(2)因为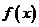 为奇函数,所以有
为奇函数,所以有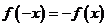 成立.
成立.
当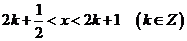 时,
时,
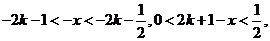
所以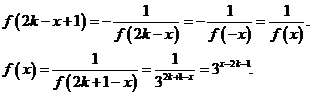
(3) 
|

|
版权所有:()
版权所有:()
20、解:(1)当a=1,b=-2时,f(x)=x2-x-3=x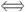 x2-2x-3=0
x2-2x-3=0
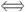 (x-3)(x+1)=0
(x-3)(x+1)=0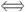 x=3或x=-1,
x=3或x=-1,
∴f(x)的不动点为x=3或x=-1.
(2)对于任意实数b,f(x)恒有两个相异不动点
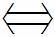 对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根
对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根
即ax2+bx+b-1=0恒有两个不等实根
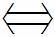 对任意实数b,Δ=b2-4a(b-1)>0恒成立
对任意实数b,Δ=b2-4a(b-1)>0恒成立
 对任意实数b,b2-4ab+4a>0恒成立
对任意实数b,b2-4ab+4a>0恒成立
 Δ′=16a2-16a<0
Δ′=16a2-16a<0
 a(a-1)<0
a(a-1)<0 0<a<1.
0<a<1.
19. 解:设投入B产品为 万,则投入A产品为
万,则投入A产品为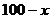 万,总收益为
万,总收益为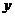 万。
万。
由题意可知: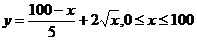 ,设
,设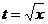 ,则
,则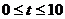 。
。
原式为: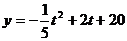 ,
,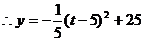 ,
,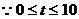 ,
,
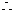 当
当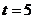 时,此时
时,此时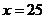 ,
,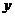 有最大值为25。
有最大值为25。
答:当投入A产品为75万,投入B产品为25万时,两种产品的年总收益最大为25万。
18.解:(1)a ≥-2
(2)由f(1+x)=f(1-x)得,
(1+x)2+a(1+x)+b=(1-x)2+a(1-x)+b,即:(a+2)x=0,
由于对任意的x都成立,∴ a=-2.
可知
f (x)=x 2-2x+b,下面证明函数f(x)在区间[1,+∞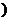 上是增函数.设
上是增函数.设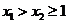 ,
,
则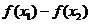 =(
=( )-(
)-(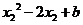 )
)
=(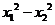 )-2(
)-2(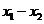 )=(
)=(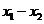 )(
)(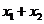 -2)
-2)
∵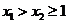 ,则
,则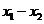 >0,且
>0,且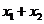 -2>2-2=0,
-2>2-2=0,
∴ 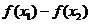 >0,即
>0,即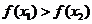 ,故函数f(x)在区间[1,+∞
,故函数f(x)在区间[1,+∞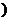 上是增函数.
上是增函数.
法2:可用导数证明
16解:p为真时: q为真时:
q为真时:
(1)p假q真: 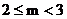
( 2)p真q假:

综上所述:m的取值范围 或
或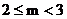
17、解:(1)由
得 推出
推出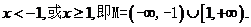
(2)由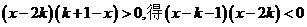
∵k<1,∴k+1>2k,故N=(2k,k+1).
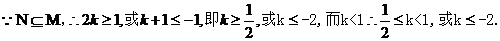
故当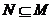 时,实数k的取值范围是
时,实数k的取值范围是
21.(满分14分)
设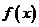 的定义域为
的定义域为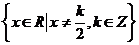 ,且
,且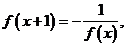 如果
如果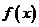 为奇函数,当
为奇函数,当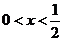 时,
时,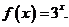
(1)求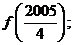
(2)当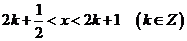 时,求
时,求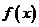
(3)是否存在这样的自然数 使得当
使得当 时,
时,
不等式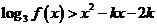 有实数解.
有实数解.
注意:请同学们将解答务必写在答卷的指定的位置上,否则不计分
|
一:选择题(本大题8小题,每题5分,共40分)
二、填空题(本大题7小题,每题5分,共35分)
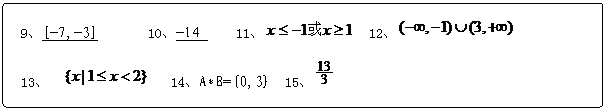
20、(满分12分)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.
已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
19. (满分13分)
某厂准备投资100万生产A,B两种新产品,据测算,投产后的年收益,A产品是总投入的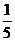 ,B产品则是总投入开平方后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大?
,B产品则是总投入开平方后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大?
注意:请同学们将解答务必写在答卷的指定的位置上,否则不计分
18.(满分12分)
已知函数f ( x )=x 2+ax+b
(1)若f (x)在[ 1,+∞)内递增,求实数a的范围。
(2)若对任意的实数x都有f (1+x)=f (1-x) 成立,
①求实数 a的值;
②证明函数f(x)在区间[1,+∞ 上是增函数.
上是增函数.
17.(满分12分)
设函数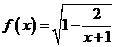 的定义域为M,
的定义域为M,
函数 的定义域为N.
的定义域为N.
(1)求集合M;
(2)若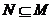 ,求实数k的取值范围.
,求实数k的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com