
21.解:(I)由a1=1, ,n=1,2,3,……,
,n=1,2,3,……,
得 ------------------------
------------------------
由
得
 -------------------------------------------
-------------------------------------------
所以an=

∴ 数列{an}的通项公式为 ;--------------------------------------
;--------------------------------------
(II)由(I)可知 是首项为
是首项为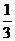 ,
,
公比为 项数为n的等比数列,-----------
项数为n的等比数列,-----------
∴  =
= -------------------------------------
-------------------------------------
20.解:(1)
 解得
解得 ------------------------------------------------------
------------------------------------------------------
 --------------------------------------------------------------------
--------------------------------------------------------------------
(2)由 得
得 -------------------------------------
-------------------------------------
当 时:
时: 或
或
当 时:
时: 或
或
当 时:
时: 或
或 -----------------------------------------------------------
-----------------------------------------------------------
19.  (Ⅰ)因为
(Ⅰ)因为 是等边三角形,
是等边三角形, ,
,
所以 ,可得
,可得 。
。
如图,取 中点
中点 ,连结
,连结 ,
, ,
,
则 ,
, ,
,
所以 平面
平面 ,
,
 所以
所以 。
......6分
。
......6分 

18. 解(1)由已知得椭圆的半长轴a=2,半焦距c= ,则半短轴b=1.
,则半短轴b=1.
又椭圆的焦点在x轴上, ∴椭圆的标准方程为 …………………………………4分
…………………………………4分
(2)设线段PA的中点为M(x,y) ,点P的坐标是(x0,y0),
由 得
得 ……………………………………………………………8分
……………………………………………………………8分
由,点P在椭圆上,得 , …………………………………………10分
, …………………………………………10分
∴线段PA中点M的轨迹方程是 .…………………………………12分
.…………………………………12分
17. 作 交BE于N,交CF于M.
交BE于N,交CF于M.
 ,
, 


 ,
,
 . ......6分
. ......6分 

在 中,由余弦定理,
中,由余弦定理,
 . ......12分
. ......12分
22. 已知函数 ,其中
,其中 .
.
(Ⅰ)当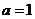 时,求曲线
时,求曲线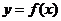 在点
在点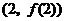 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数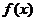 的单调区间与极值.
的单调区间与极值.
高三9月份月考考数学文试卷答案评分标准 2009.9.
21.数列{an}的前n项和为Sn,且a1=1, ,n=1,2,3,……,
,n=1,2,3,……,
求 (I)数列{an}的通项公式;
(II) 的值.
的值.
20. 已知函数 ,且方程
,且方程 有两个实根为
有两个实根为 ,
,
(1)求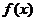 的解析式(2)设
的解析式(2)设 ,解关于
,解关于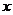 的不等式:
的不等式:
19. 如图,在三棱锥 中,⊿
中,⊿ 是等边三角形,∠PAC=∠PBC=90 º
是等边三角形,∠PAC=∠PBC=90 º
 (Ⅰ)证明:AB⊥PC
(Ⅰ)证明:AB⊥PC
(Ⅱ)若 ,且平面
,且平面 ⊥平面
⊥平面 ,
,
求三棱锥 体积。
体积。
18. 已知在平面直角坐标系 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为 ,
,
右顶点为 ,设点
,设点 .
.
(1)求该椭圆的标准方程;
(2)若 是椭圆上的动点,求线段
是椭圆上的动点,求线段 中点
中点 的轨迹方程。
的轨迹方程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com