
8.若集合 , 则
, 则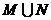 等于 __________;
等于 __________;
7.已知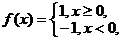 则不等式
则不等式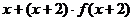 ≤5的解集是
。
≤5的解集是
。
6.某公司一年购买某种货物400吨,每次都购买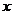 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为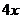 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则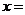 吨;
吨;
5.若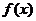 的定义域为[0,1],则
的定义域为[0,1],则 的定义域为
;
的定义域为
;
4.已知函数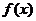 满足
满足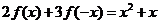 ,则
,则 ;
;
3. 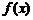 =
= ,若
,若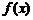
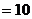 ,则
,则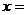 ;
;
2.已知集合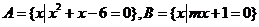 ,且
,且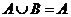 ,则
,则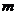 的取值的集合
的取值的集合
是 ;
1..已知函数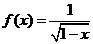 的定义域为
的定义域为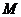 ,
, 的定义域为
的定义域为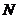 ,则
,则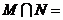 ;
;
22、如图,在矩形ABCD中,AB=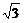 ,BC=a,又PA⊥平面ABCD,PA=4.
(1)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(2)当BC上存在唯一点Q,使PQ⊥QD时,求异面直线AQ与PD所成角的大小;
(3)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.
,BC=a,又PA⊥平面ABCD,PA=4.
(1)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(2)当BC上存在唯一点Q,使PQ⊥QD时,求异面直线AQ与PD所成角的大小;
(3)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.
解:
(1)、以 为x、y、z轴建立空间直角坐标系,则
为x、y、z轴建立空间直角坐标系,则
B(0,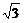 ,0),C(-a,
,0),C(-a,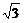 ,0),D(-a,0,0),P(0,0,4)
,0),D(-a,0,0),P(0,0,4)
设Q(t,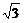 ,0),则
,0),则  =(t,
=(t,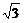 ,-4),
,-4),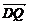 =(t+a,
=(t+a,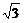 ,0)
∵PQ⊥QD,∴
,0)
∵PQ⊥QD,∴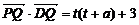 =0 即t2+at+3=0 ①
∴△=a2-12≥0 Þ a≥2
=0 即t2+at+3=0 ①
∴△=a2-12≥0 Þ a≥2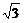 .
.
(2)、∵BC上存在唯一点Q,使PQ⊥QD,
∴△=a2-12=0 Þ a=2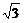 ,t=-
,t=-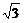
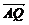 =(-
=(-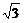 ,
,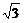 ,0) ,
,0) , =(-2
=(-2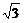 ,0,-4)
∴cos
,0,-4)
∴cos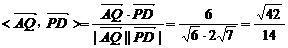 故异面直线AQ与PD所成角为arccos
故异面直线AQ与PD所成角为arccos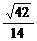 .
.
(3)、过Q作QM∥CD交AD于M,则QM⊥AD,M(t,0,0) ∵PA⊥平面ABCD,∴PA⊥QM,又QM⊥AD,∴QM⊥平面PAD 过M作MN⊥PD于N,连结NQ,由三垂线定理知QN⊥PD ∴∠MNQ是二面角A-PD-Q的平面角
设N (m,0,n),则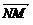 =(t-m,0,-n),
=(t-m,0,-n),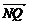 =(t-m,
=(t-m,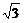 ,-n)
,-n)
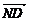 =(-4-m,0,-n) ∵MN⊥PD,ND、PD共线,∴
=(-4-m,0,-n) ∵MN⊥PD,ND、PD共线,∴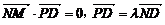
得:m+n-t=0,m-n=4 ② 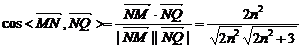
由①得:t=-1或t=-3,由②得:n=2+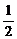 t
t
当t=-1时,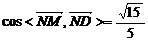 ,当t=-3时,
,当t=-3时,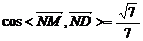
∴二面角A-PD-Q的大小为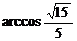 或
或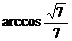 .
.
21、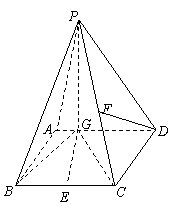 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4, ,BG⊥GC,GB=GC=2,E是BC的中点.
,BG⊥GC,GB=GC=2,E是BC的中点.
(1)求异面直线GE与PC所成的角;
(2)求点D到平面PBG的距离;
(3)若F点是棱PC上一点,且DF⊥GC,求 的值.
的值.
解:(1)解:以G点为原点,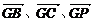 为x轴、y轴、z轴建立空间直角坐标系,
为x轴、y轴、z轴建立空间直角坐标系,
则B(2,0,0),C(0,2,0),P(0,0,4), 故E(1,1,0) 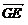 =(1,1,0),
=(1,1,0),
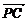 =(0,2,4)
=(0,2,4) 
∴GE与PC所成的角为arccos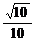 .
.
(2)解:平面PBG的单位法向量n=(0,±1,0) ∵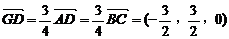
∴点D到平面PBG的距离为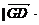 n |=
n |=
(3)解:设F(0,y,z),则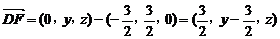
∵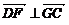 ,∴
,∴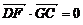 , 即
, 即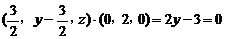 ,∴
,∴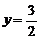 又
又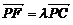 ,即(0,
,即(0, ,z-4)=λ(0,2,-4),∴z=1,
,z-4)=λ(0,2,-4),∴z=1,
故F(0, ,1)
,1)  ,∴
,∴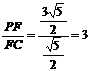
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com