
1.点面结合
典型材料和一般材料结合,才能使文章在思想内容上既有深度又有广度。
[举例]
高考优秀作文《心灵的选择》--
面对鸦片泛滥,长此下去,全中国将无御敌之兵且无充饷之银的危难境况,林则徐毅然挺身而出,虎门销烟壮举威慑中外;面对元人的种种威逼利诱,文天祥决然赴义,“臣心一片磁针石,不指南方不肯休。”
文章在“点”的列举之后,以点带面,继续扩展阐发道:
从古至今,有多少豪杰,多少壮士为了心中的高尚情操,为了祖国的尊严,面对生与死的激烈碰撞,他们抛头颅、洒热血,蹈死不顾,至死不悔。这不悔正是他们心中做出的正确的选择。他们的豪言壮语、英勇事迹激励着一代代成长中的青年,他们的选择已在我们的心中深深地扎下了根,他们的举动直可惊天地、泣鬼神。与天地兮比寿、与日月兮齐光。
将“面”铺开,点面结合,使文章的论述无懈可击。
(三)解答题
10.某科技小组有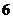 名同学,现从中选出
名同学,现从中选出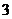 人去参观展览,至少有
人去参观展览,至少有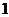 名女生入选时的不同选法有
名女生入选时的不同选法有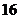 种,求该科技小组中女生的人数。
种,求该科技小组中女生的人数。
思路:分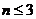 和
和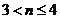 两种情况讨论。 答案:女生的人数是2。
两种情况讨论。 答案:女生的人数是2。
(二)填空题(列式并算出结果)
4.已知甲、乙两组各有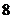 人,现从每组抽取
人,现从每组抽取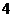 人进行计算机知识竞赛,比赛成员的组成共有
人进行计算机知识竞赛,比赛成员的组成共有
种可能。 答案:
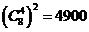
5.在一次考试的选做题部分,要求在第1题的4个小题中选做3个小题,在第2题的3个小题中选做2个小题,第3题的2个小题中选做1个小题,有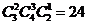 种不同的选法。
种不同的选法。
6.从1,3,5,7,9中任取3个数字,从2,4,6,8中任取2个数字,一共可以组成
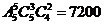 个没有重复数字的五位数。
个没有重复数字的五位数。
7.正六边形的中心和顶点共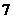 个点,以其中三个点为顶点的三角形共有
个点,以其中三个点为顶点的三角形共有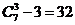 个。
个。
8.从5名男生和4名女生中选出4人去参加辩论比赛。
(1)如果4人中男生和女生各选2人,有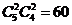 种选法;
种选法;
(2)如果男生中的甲与女生中的乙必须在内,有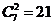 种选法;
种选法;
(3)如果男生中的甲与女生中的乙至少要有1人在内,有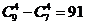 种选法;
种选法;
(4)如果4人中必须既有男生又有女生,有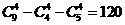 种选法。
种选法。
9.在200件产品中,有2件次品。从中任取5件,
(1)“其中恰有2件次品”的抽法有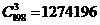 种;
种;
(2)“其中恰有1件次品”的抽法有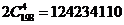 种;
种;
(3)“其中没有次品”的抽法有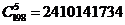 种;
种;
(4)“其中至少有1件次品”的抽法有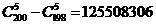 种。
种。
(一)选择题
1.有两条平行直线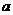 和
和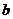 ,在直线
,在直线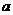 上取
上取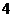 个点,直线
个点,直线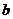 上取
上取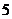 个点,以这些点为顶点作三角形,这样的三角形共有 (A)
个点,以这些点为顶点作三角形,这样的三角形共有 (A)
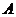 .
.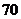
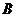 .
.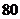
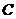 .
.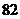
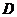 .
.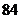
2.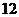 名同学分别到三个不同的路口进行车流量的调查,若每个路口
名同学分别到三个不同的路口进行车流量的调查,若每个路口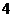 人,则不同的分配方
人,则不同的分配方
案有 (A)
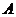 .
.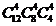 种
种 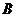 .
.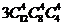 种
种 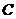 .
.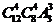 种
种 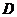 .
.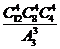 种
种
3.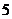 本不同的书,全部分给
本不同的书,全部分给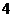 个学生,每个学生至少一本,不同分法的种数为 (B)
个学生,每个学生至少一本,不同分法的种数为 (B)
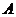 .
.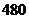
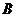 .
.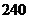
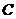 .
.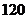
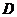 .
.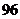
3.对有特殊要求的问题,可优先满足特殊要求,也可考虑“去杂法”。
2.对较复杂的组合应用题,要能根据事件的发生、发展过程对解决问题的办法进行恰当地
分类或分步,利用分类计数原理和分步计数原理解决问题;
1.准确分析事件的发生、发展过程,弄清要解决的问题是否与取出的元素的顺序有关,把
实际问题抽象成组合问题;
2.以一个正方体的8个顶点连成的异面直线共有 对。
解:由上题可知以一个正方体的顶点为顶点的四面体共有58个,每个四面体的四条棱可以组成3对异面直线,因此以一个正方体的8个顶点连成的异面直线共有3×58=174对。
另解: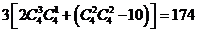 对。
对。
1.以一个正方体的顶点为顶点的四面体共有 个。
解:正方体有8个顶点,任取4个顶点的组合数为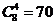 个,
个,
其中四点共面的情况分2类:构成表面的有6组;构成对角面的有6组,
所以,能形成四面体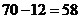 (个).
(个).
(二)新课讲解:
例1 100件产品中,有98件合格品,2件次品。从这100件产品中任意抽出3件.
(1)一共有多少种不同的抽法;
(2)抽出的3件都不是次品的抽法有多少种?
(3)抽出的3件中恰好有1件是次品的抽法有多少种?
(4)抽出的3件中至少有1件是次品的取法有多少种?
解:(1)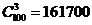 ;(2)
;(2)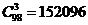 ;(3)
;(3)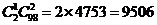 ;
;
(4)解法一:(直接法)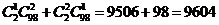 ;
;
解法二:(间接法) .
.
例2 从编号为1,2,3,…,10,11的共11个球中,取出5个球,使得这5个球的编号之和为奇数,则一共有多少种不同的取法?
解:分为三类:1奇4偶有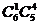 ; 3奇2偶有
; 3奇2偶有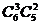 ; 5奇1偶有
; 5奇1偶有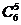 ,
,
∴一共有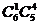 +
+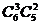 +
+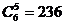 .
.
例3 现有8名青年,其中有5名能胜任英语翻译工作;有4名青年能胜任德语翻译工作(其中有1名青年两项工作都能胜任),现在要从中挑选5名青年承担一项任务,其 中3名从事英语翻译工作,2名从事德语翻译工作,则有多少种不同的选法?
解:我们可以分为三类:
①让两项工作都能担任的青年从事英语翻译工作,有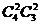 ;
;
②让两项工作都能担任的青年从事德语翻译工作,有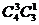 ;
;
③让两项工作都能担任的青年不从事任何工作,有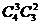 ,
,
∴一共有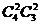 +
+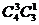 +
+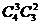 =42种方法.
=42种方法.
例4 甲、乙、丙三人值周,从周一至周六,每人值两天,但甲不值周一,乙不值周六,问可以排出多少种不同的值周表 ?
解法一:(排除法)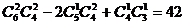 .
.
解法二:分为两类:一类为甲不值周一,也不值周六,有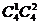 ;
;
另一类为甲不值周一,但值周六,有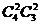 ,∴一共有
,∴一共有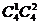 +
+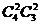 =42种方法.
=42种方法.
例5 6本不同的书全部送给5人,每人至少1本,有多少种不同的送书方法?
解:第一步:从6本不同的书中任取2本“捆绑”在一起看成一个元素有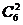 种方法;
种方法;
第二步:将5个“不同元素(书)”分给5个人有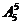 种方法.
种方法.
根据分步计数原理,一共有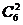
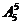 =1800种方法.
=1800种方法.
变题1:6本不同的书全部送给5人,有多少种不同的送书方法?
变题2:5本不同的书全部送给6人,每人至多1本,有多少种不同的送书方法?
变题3:5本相同的书全部送给6人,每人至多1本,有多少种不同的送书方法?
答案:1.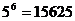 ; 2.
; 2.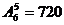 ; 3.
; 3.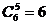 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com