11．用三段论证明函数y＝－x²+2x在(－∞，1]上是增函数．

[证明]　任取x₁、x₂∈(－∞，1]，且x₁＜x₂，

f(x₁)－f(x₂)＝(－x+2x₁)－(－x+2x₂)

＝(x₂－x₁)(x₂+x₁－2)．

因为x₁＜x₂，所以x₂－x₁＞0；

因为x₁、x₂≤1，x₁≠x₂，所以(x₂+x₁－2)＜0.

因此，f(x₁)－f(x₂)＜0，即f(x₁)＜f(x₂)．

于是根据“三段论”，得f(x)＝－x²+2x在(－∞，1]上是增函数．

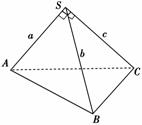
10．(2008·深圳市高三年级第一次调研考试)在Rt△ABC中，两直角边分别为a、b，设h为斜边上的高，则＝+；由此类比：三棱锥S－ABC中的三条侧棱SA、SB、SC两两垂直，且长度分别为a、b、c，设棱锥底面ABC上的高为h，则得出的正确结论为________．

[解析]　在Rt△ABC中，CD为斜边AB边上的高．

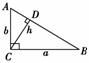
则CD·AB＝AC·BC

∴＝

故＝＝＝＝+

在三棱锥S－ABC中，

由SA、SB、SC两两垂直得

V_S－ABC＝V_C－SAB，即hS_ABC＝(SA·SB)SC

∴＝

＝

＝++.

[答案]　＝++

9．已知圆的方程是x²+y²＝r²，则经过圆上一点M(x₀，y₀)的切线方程为x₀x+y₀y＝r².类比上述性质，可以得到椭圆+＝1类似的性质为________．

[解析]　圆的性质中，经过圆上一点M(x₀，y₀)的切线方程就是将圆的方程中的一个x与y分别用M(x₀，y₀)的横坐标与纵坐标替换．

故可得椭圆+＝1类似的性质为：

过椭圆+＝1上一点P(x₀，y₀)的切线方程为+＝1.

[答案]　过椭圆+＝1上一点P(x₀，y₀)的切线方程为+＝1

8．如图，这是一个正六边形的序列：

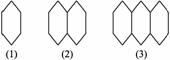
则第(n)个图形的边数是________．

[解析]　设a_n是第(n)个图形的边数，则a₁＝6，a₂＝6+5，a₃＝6+5×2，…，归纳得a_n＝6+5(n－1)＝5n+1.

[答案]　5n+1

7．在平面几何中，△ABC的内角平分线CE分AB所成线段的比＝，把这个结论类比到空间：在三棱锥A－BCD中(如图所示)，而DEC平分二面角A－CD－B且与AB相交于E，则得到的类比的结论是________．

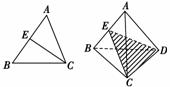
[解析]　由类比推理可知．

[答案]　＝

6．已知整数的数对列如下：(1,1)，(1,2)，(2,1)，(1,3)，(2,2)，(3,1)，(1,4)，(2,3)，(3,2)，(4,1)，(1,5)，(2,4)，…则第60个数对是

(　)

A．(3,8)　 B．(4,7)　 C．(4,8)　 D．(5,7)

[解析]　观察可知横坐标和纵坐标之和为2的数对有1个，和为3的数对有2个，和为4的数对有3个，和为5的数对有4个，依此类推和为n+1的数对有n个，多个数对的排序是按照横坐标依次增大的顺序来排的，由＝60⇒n(n+1)＝120，n∈Z，n＝10时，＝55个数对，还差5个数对，且这5个数对的横、纵坐标之和为12，它们依次是(1,11)，(2,10)，(3,9)，(4,8)，(5,7)，

∴第60个数对是(5,7)．

[答案]　D

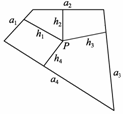
5．(2007年广州一模)如图，面积为S的平面凸四边形的第i条边的边长记为a_i(i＝1,2,3,4)，此四边形内任一点P到第i条边的距离记为hi(i＝1,2,3,4)，若＝＝＝＝k，则(ih_i)＝.类比以上性质，体积为V的三棱锥的第i个面的面积记为S_i(i＝1,2,3,4)，此三棱锥内任一点Q到第i个面的距离记为H_i(i＝1,2,3,4)，若＝＝＝＝K，则(iH_i)＝

(　)

A.　 B.　 C.　 D.

[解析]　V_三棱锥＝(S₁H₁+S₂H₂+S₃H₃+S₄H₄)

＝K(H₁+2H₂+3H₃+4H₄)

＝K(iH_i)

∴(iH_i)＝，故选B.

[答案]　B

4．给出下列三个类比结论．

①(ab)ⁿ＝aⁿbⁿ与(a+b)ⁿ类比，则有(a+b)ⁿ＝aⁿ+bⁿ；

②log_a(xy)＝log_ax+log_ay与sin(α+β)类比，则有sin(α+β)＝sinαsinβ；

③(a+b)²＝a²+2ab+b²与(a+b)²类比，则有(a+b)²＝a²+2a·b+b².

其中结论正确的个数是

(　)

A．0　 B．1　 C．2　 D．3

[解析]　③正确．

[答案]　B

3．下列在向量范围内成立的命题类比地推广到复数范围内，仍然为真命题的个数是

(　)

①|a·b|≤|a|·|b|；　②|a+b|≤|a|+|b|；　③a²≥0；　④(a+b)²＝a²+2a·b+b²

A．1　 B．2　 C．3　 D．4

[答案]　C

2．已知a₁＝1，a_n+1>a_n，且(a_n+1－a_n)²－2(a_n+1+a_n)+1＝0，计算a₂，a₃，猜想a_n＝

(　)

A．n　　 　　　　　　　　　　　　　　　 B．n²

C．n³　 　　　　　　　　　　　　　　　　 D.－

[解析]　∵(a₂－a₁)²－2(a₂+a₁)+1＝0，a₁＝1

∴a－4a₂＝0　∴a₂＝4或a₂＝0(舍去)

又∵(a₃－a₂)²－2(a₃+a₂)+1＝0

∴a－10a₃+9＝0

∴a₃＝9或a₃＝1(舍去)

故猜想a_n＝n²，选B.

[答案]　B