
5.(宁波市2008学年度第一学期高三期末数(文理))(本题15分)如图,椭圆长轴端点为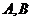 ,
,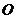 为椭圆中心,
为椭圆中心, 为椭圆的右焦点,
为椭圆的右焦点,
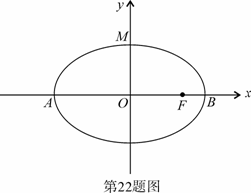 且
且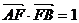 ,
,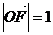 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)记椭圆的上顶点为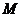 ,直线
,直线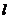 交椭圆于
交椭圆于 两点,问:是否存在直线
两点,问:是否存在直线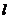 ,使点
,使点 恰为
恰为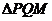 的垂心?若存在,求出直线
的垂心?若存在,求出直线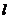 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 解:(1)设椭圆方程为
解:(1)设椭圆方程为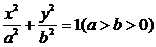
由题意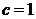
又∵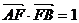 即
即 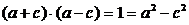
∴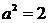 故椭圆方程为
故椭圆方程为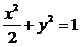 …………6分
…………6分
(2)假设存在直线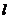 交椭圆于
交椭圆于 两点,且
两点,且 恰为
恰为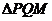 的垂心,则
的垂心,则
设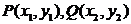 ,∵
,∵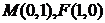 ,故
,故 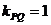 ……………8分(第5题)
……………8分(第5题)
于是设直线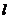 为
为 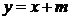 ,由
,由 得
得
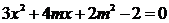 …………10分
…………10分
∵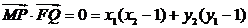 又
又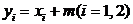
得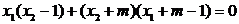 即
即
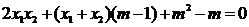 由韦达定理得
由韦达定理得
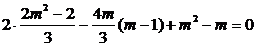
解得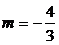 或
或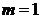 (舍) 经检验
(舍) 经检验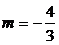 符合条件
符合条件
则直线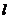 的方程为:
的方程为: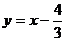 ………15分
………15分
4. (浙江省09年高考省教研室第一次抽样测试数学试题(理))已知抛物线C
(浙江省09年高考省教研室第一次抽样测试数学试题(理))已知抛物线C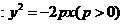 上横坐标为
上横坐标为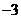 的一点,与其焦点的距离为4.(1)求
的一点,与其焦点的距离为4.(1)求 的值;(2)设动直线
的值;(2)设动直线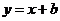 与抛物线C相交于A、B两点,问在直线
与抛物线C相交于A、B两点,问在直线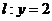 上是否存在与
上是否存在与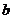 的取值无关的定点M,使得
的取值无关的定点M,使得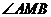 被直线
被直线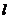 平分?若存在,求出点M的坐标;若不存在,说明理由.
平分?若存在,求出点M的坐标;若不存在,说明理由.
解析:(1)由已知得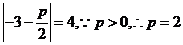
(2)令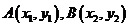 ,设存在点
,设存在点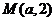 满足条件,由已知得
满足条件,由已知得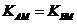 ,即有
,即有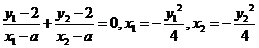 ;整理得
;整理得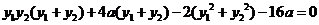 ;由
;由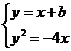 得
得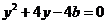 ,即
,即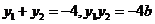 有
有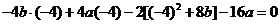 ,
, ,因此存在点M(
,因此存在点M(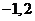 )满足题意.
)满足题意.
3. (温州市十校2008学年高三第一学期期初联考
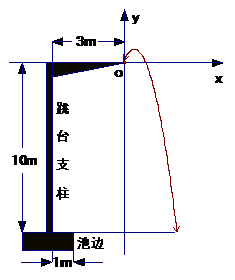
数学试题(文))2008年北京奥运会中国跳水梦之队取得了辉煌的成绩。
(温州市十校2008学年高三第一学期期初联考
数学试题(文))2008年北京奥运会中国跳水梦之队取得了辉煌的成绩。
据科学测算,跳水运动员进行10米跳台跳水训练时,
身体(看成一点)在空中的运动轨迹(如图所示)是
一经过坐标原点的抛物线(图中标出数字为已知条件),
且在跳某个规定动作时,正常情况下运动员在空中的最
高点距水面 米,入水处距池边4米,同时运动员在
米,入水处距池边4米,同时运动员在
距水面5米或5米以上时,必须完成规定的翻腾动作,
并调整好入水姿势,否则就会出现失误。
(1)求抛物线的解析式;
(2)在某次试跳中,测得运动员在空中
的运动轨迹为(1)中的抛物线,且运动员在空中
调整好入水姿势时距池边的水平距离为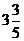 米,问
米,问
此次跳水会不会失误?请通过计算说明理由; (第3题图)
(3)某运动员按(1)中抛物线运行,要使得此次跳水成功,他在空中调整好入水姿势时,距池边的水平距离至多应为多大?
解:(1)由已知可设抛物线方程为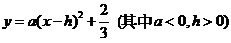
又抛物线过(0,0)和(2,-10) (2分)
代入解得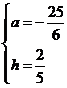 ,
,
所以解析式为: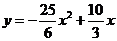 (5分)
(5分)
(2)当运动员在空中距池边的水平距离为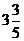 米时,即
米时,即 时,
时,
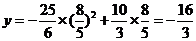 (7分)
(7分)
所以此时运动员距水面距离为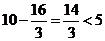 ,故此次跳水会出现失误 (10分)
,故此次跳水会出现失误 (10分)
(3)要使得某次跳水成功,必须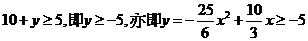
解不等式得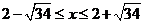
所以运动员此时距池边的水平距离最大为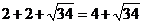 米。 (15分)
米。 (15分)
2.(2008学年第一学期十校高三期末联考数学试题(文))(15分)在平面直角坐标系xOy中,已知点A(-1, 0)、B(1, 0), 动点C满足条件:△ABC的周长为2+2.记动点C的轨迹为曲线W.
(Ⅰ)求W的方程;
(Ⅱ)经过点(0, )且斜率为k的直线l与曲线W 有两个不同的交点P和Q,
求k的取值范围;
(Ⅲ)已知点M(,0),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量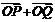 与
与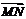 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.
解(Ⅰ) 设C(x, y),
∵ 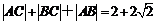 ,
, 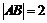 ,
,
∴ 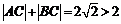 ,
,
∴ 由定义知,动点C的轨迹是以A、B为焦点,长轴长为2的椭圆除去与x轴的两个交点.
∴ 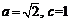 . ∴
. ∴
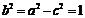 .
.
∴ W: 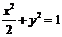
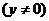 . …………………………………………… 5分
. …………………………………………… 5分
(Ⅱ) 设直线l的方程为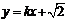 ,代入椭圆方程,得
,代入椭圆方程,得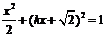 .
.
整理,得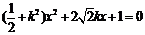 .
①………………………… 7分
.
①………………………… 7分
因为直线l与椭圆有两个不同的交点P和Q等价于
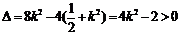 ,解得
,解得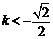 或
或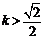 .
.
∴ 满足条件的k的取值范围为 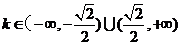 ………… 10分
………… 10分
(Ⅲ)设P(x1,y1),Q(x2,y2),则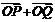 =(x1+x2,y1+y2),
=(x1+x2,y1+y2),
由①得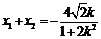 .
②
.
②
又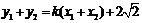 ③
③
因为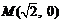 ,
,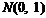 , 所以
, 所以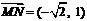 .……………………… 12分
.……………………… 12分
所以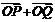 与
与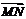 共线等价于
共线等价于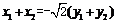 .
.
将②③代入上式,解得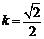 .
.
所以不存在常数k,使得向量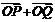 与
与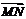 共线. ……………………15分
共线. ……………………15分
1.((2008学年第一学期十校高三期末联考数学试题(理))本小题满分15分)在平面直角坐标系xOy中,已知点A(-1, 0)、B(1, 0), 动点C满足
条件:△ABC的周长为2+2.记动点C的轨迹为曲线W.
(Ⅰ) 求W的方程;
(Ⅱ) 经过点(0, )且斜率为k的直线l与曲线W 有两个不同的交点P和Q,求k
的取值范围;
(Ⅲ)已知点M(,0),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量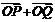
与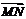 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.
解: (Ⅰ) 设C(x, y),
∵ 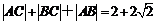 ,
, 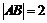 ,
,
∴ 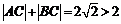 ,
,
∴ 由定义知,动点C的轨迹是以A、B为焦点,长轴长为2的椭圆除去与x轴的两个交点.
∴ 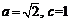 . ∴
. ∴ 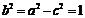 .
.
∴ W: 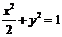
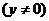 . …………………………………………… 5分
. …………………………………………… 5分
(Ⅱ) 设直线l的方程为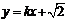 ,代入椭圆方程,得
,代入椭圆方程,得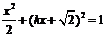 .
.
整理,得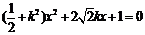 .
①………………………… 7分
.
①………………………… 7分
因为直线l与椭圆有两个不同的交点P和Q等价于
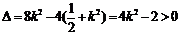 ,解得
,解得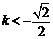 或
或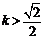 .
.
∴ 满足条件的k的取值范围为 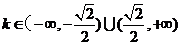 ………… 10分
………… 10分
(Ⅲ)设P(x1,y1),Q(x2,y2),则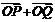 =(x1+x2,y1+y2),
=(x1+x2,y1+y2),
由①得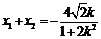 .
②
.
②
又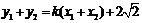 ③
③
因为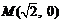 ,
,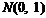 , 所以
, 所以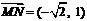 .……………………… 12分
.……………………… 12分
所以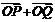 与
与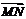 共线等价于
共线等价于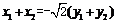 .
.
将②③代入上式,解得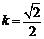 .
.
所以不存在常数k,使得向量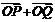 与
与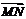 共线. ……………………15分
共线. ……………………15分
21.解:(1)设 ,则由
,则由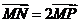 得
得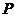 为
为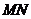 中点,所以
中点,所以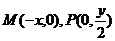
又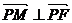 得
得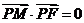 ,
,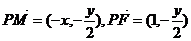 ,
,
所以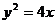 (
(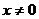 ).
………………6分
).
………………6分
(2)由(1)知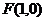 为曲线
为曲线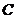 的焦点,由抛物线定义知,抛物线上任一点
的焦点,由抛物线定义知,抛物线上任一点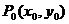 到
到 的距离等于其到准线的距离,即
的距离等于其到准线的距离,即 ,
,
所以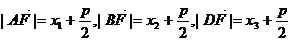 ,
,
根据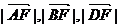 成等差数列,得
成等差数列,得 , ………………10分
, ………………10分
直线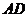 的斜率为
的斜率为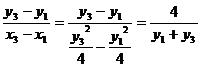 ,
,
所以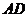 中垂线方程为
中垂线方程为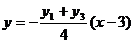 ,
………………12分
,
………………12分
又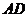 中点
中点 在直线上,代入上式得
在直线上,代入上式得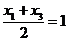 ,即
,即 ,
,
所以点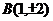 .
………………15分
.
………………15分
21.(本小题满分15分)设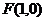 ,点
,点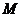 在
在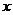 轴上,点
轴上,点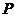 在
在 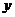 轴上,且
轴上,且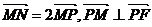
(1)当点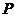 在
在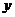 轴上运动时,求点
轴上运动时,求点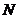 的轨迹
的轨迹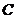 的方程;
的方程;
(2)设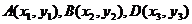 是曲线
是曲线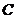 上的点,且
上的点,且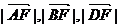 成等差数列,当
成等差数列,当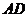 的垂直平分线与
的垂直平分线与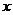 轴交于点
轴交于点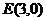 时,求
时,求 点坐标.
点坐标.
7.
 ………………5分
………………5分
|
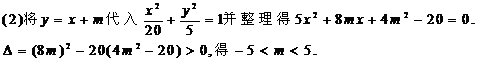
|
|

6.(宁波文(本题15分))如图,椭圆长轴端点为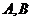 ,
,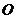 为椭圆中心,
为椭圆中心, 为椭圆的右焦点,
为椭圆的右焦点,
 且
且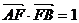 ,
,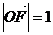 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)记椭圆的上顶点为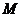 ,直线
,直线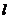 交椭圆于
交椭圆于 两点,问:是否存在直线
两点,问:是否存在直线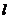 ,使点
,使点 恰为
恰为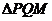 的垂心?若存在,求出直线
的垂心?若存在,求出直线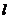 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
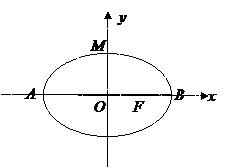 6 解:(1)设椭圆方程为
6 解:(1)设椭圆方程为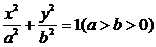
由题意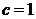
又∵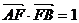 即
即 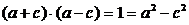
∴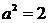 故椭圆方程为
故椭圆方程为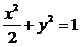 …………6分
…………6分
(2)假设存在直线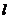 交椭圆于
交椭圆于 两点,且
两点,且 恰为
恰为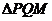 的垂心,则
的垂心,则
设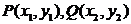 ,∵
,∵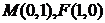 ,故
,故 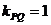 ……………8分
……………8分
于是设直线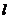 为
为 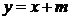 ,由
,由 得
得
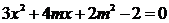 …………10分
…………10分
∵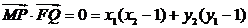 又
又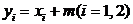
得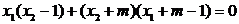 即
即
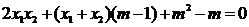 由韦达定理得
由韦达定理得
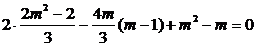
解得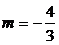 或
或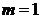 (舍) 经检验
(舍) 经检验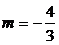 符合条件
符合条件
则直线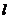 的方程为:
的方程为: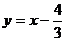 ………15分
………15分
7(本题满分15分)如图,已知椭圆的中心在原点,焦点在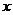 轴上,离心率为
轴上,离心率为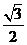 ,且经过点
,且经过点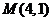 . 直线
. 直线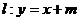 交椭圆于
交椭圆于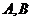 两不同的点.
两不同的点.

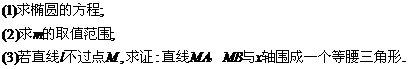
5.(宁波市2008学年度第一学期期末试卷高三数学(理科))
(本题15分)如图,椭圆长轴端点为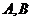 ,
,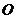 为椭圆中心,
为椭圆中心, 为椭圆的右焦点,
为椭圆的右焦点,
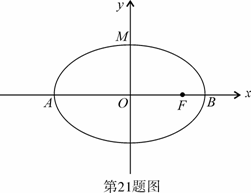 且
且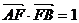 ,
,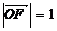 .
.
(1)求椭圆的标准方程;
(2)记椭圆的上顶点为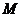 ,直线
,直线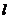 交椭圆于
交椭圆于 两点,问:是否存在直线
两点,问:是否存在直线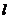 ,使点
,使点 恰为
恰为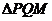 的垂心?若存在,求出直线
的垂心?若存在,求出直线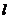 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
5解:(1)如图建系,设椭圆方程为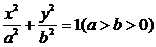 ,则
,则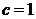
又∵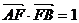 即
即 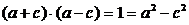
 ∴
∴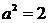
故椭圆方程为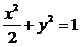 …………6分
…………6分
(2)假设存在直线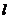 交椭圆于
交椭圆于 两点,且
两点,且 恰为
恰为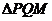 的垂心,则
的垂心,则
设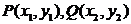 ,∵
,∵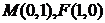 ,故
,故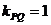 , ……8分
, ……8分
于是设直线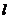 为
为 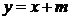 ,由
,由 得
得
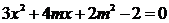 …………………………………10分
…………………………………10分
∵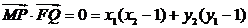 又
又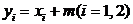
得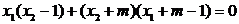 即
即
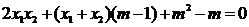 由韦达定理得
由韦达定理得
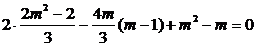
解得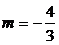 或
或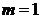 (舍) 经检验
(舍) 经检验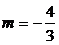 符合条件………15分
符合条件………15分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com