
6.设f(x)定义在R上的偶函数,且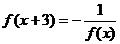 ,又当x∈(0,3]时,f(x)=2x,则f(2007)= 。
,又当x∈(0,3]时,f(x)=2x,则f(2007)= 。
答案提示:1、A;由f(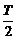 )=f(-
)=f(-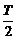 +T)=f(-
+T)=f(-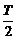 )=-f(
)=-f(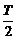 ),知f(
),知f(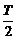 )=0.(或取特殊函数f(x)=sinx)
)=0.(或取特殊函数f(x)=sinx)
5.对任意x∈R,f(x)=f(x-1)+f(x+1)且f(0)=6,f(4)=3,则f(69)=
4.已知函数f(x)是偶函数,且等式f(4+x)=f(4-x),对一切实数x成立,写出f(x)的一个最小正周
3.设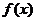 是定义在
是定义在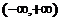 上,以2为周期的周期函数,且
上,以2为周期的周期函数,且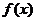 为偶函数,在区间[2,3]上,
为偶函数,在区间[2,3]上,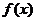 =
=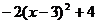 ,则
,则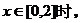
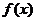 =
=
2.(2004天津)定义在R上的函数f(x)既是偶函数又是周期函数.若f(x)的最小正周期是π,且当x∈[0,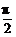 ]时,f(x)=sinx,则f(
]时,f(x)=sinx,则f(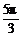 )的值为
)的值为
A.-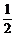 B.
B.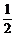 C.-
C.-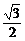 D.
D.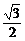
[填空题]
1.f(x)是定义在R上的奇函数,它的最小正周期为T,则f(-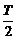 )的值为
)的值为
A.0 B.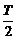 C.T D.-
C.T D.-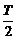
3.函数的周期性与图象的对称性之间的关系;
同步练习 2.7 函数的周期性
[选择题]
2.用周期的定义求函数的周期;
1.函数的周期性及有关概念;
2.注意既得关系式的连续使用.
[例3]若函数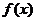 在R上是奇函数,且在
在R上是奇函数,且在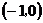 上是增函数,且
上是增函数,且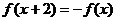 .
.
①求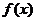 的周期;
的周期;
②证明f(x)的图象关于点(2k,0) 中心对称;关于直线x=2k+1轴对称, (k∈Z );
③讨论f(x)在(1,2)上的单调性;
解: ①由已知f(x)=-f(x+2)=f(x+2+2)=f(x+4),故周期T=4.
②设P(x,y)是图象上任意一点,则y=f(x),且P关于点(2k,0)对称的点为P1(4k-x,-y).P关于直线x=2k+1对称的点为P2(4k+2-x,y).
∵f(4k-x)=f(-x)=-f(x)=-y,∴点P1在图象上,图象关于点(2k,0)对称.
又f(x)是奇函数,f(x+2)=-f(x)=f(-x)
∴f(4k+2-x)=f(2-x)=f(x)=y, ∴点P2在图象上,图象关于直线2k+1对称.
③设1<x1<x2<2,则-2<-x2<-x1<-1, 0<2-x2<2-x1<1.
∵f(x)在(-1,0)上递增, ∴f(2-x1)<f(2-x2)……(*)
又f(x+2)=-f(x)=f(-x) ∴f(2-x1)=f(x1), f(2-x2)=f(x2).
(*)为f(x2)<f(x1),f(x)在(1,2)上是减函数.
提炼方法:总结解周期性、单调性及图象对称性的方法。
[研究.欣赏]已知函数y=f(x)是定义在R上的周期函数,周期T=5,函数y=f(x)(-1≤x≤1)是奇函数.又知y=f(x)在[0,1]上是一次函数,在[1,4]上是二次函数,且在x=2时函数取得最小值-5.
①
证明: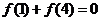 ;②求
;②求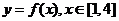 的解析式;
的解析式;
③求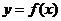 在
在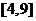 上的解析式.
上的解析式.
解:∵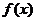 是以
是以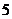 为周期的周期函数,且在[-1,1]上是奇函数,∴
为周期的周期函数,且在[-1,1]上是奇函数,∴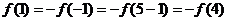 ,∴
,∴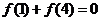 .
.
②当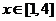 时,由题意可设
时,由题意可设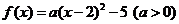 ,
,
由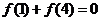 得
得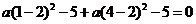 ,∴
,∴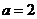 ,
,
∴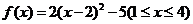 .
.
③∵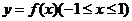 是奇函数,∴
是奇函数,∴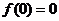 ,
,
又知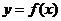 在
在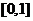 上是一次函数,∴可设
上是一次函数,∴可设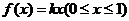 ,而
,而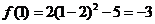 ,
,
∴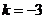 ,∴当
,∴当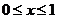 时,
时,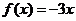 ,
,
从而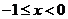 时,
时,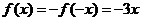 ,故
,故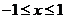 时,
时,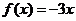 .
.
∴当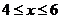 时,有
时,有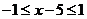 ,∴
,∴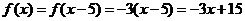 .
.
当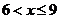 时,
时,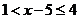 ,
,
∴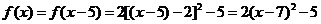
∴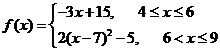 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com