
19. 设函数 ,曲线
,曲线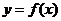 在点
在点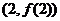 处的切线方程为
处的切线方程为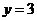 。
。
(1)求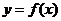 的解析式;
的解析式;
(2)证明:曲线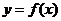 的图像是一个中心对称图形,并求其对称中心;
的图像是一个中心对称图形,并求其对称中心;
(3)证明:曲线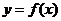 上任一点的切线与直线
上任一点的切线与直线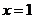 和直线
和直线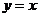 所围三角形的面积为定值,并求出此定值。
所围三角形的面积为定值,并求出此定值。
20:已知函数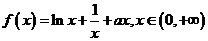 (a为实常数).
(a为实常数).
(Ⅰ)当a=0时,求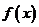 的最小值;高.考.资.源网
的最小值;高.考.资.源网
(Ⅱ)若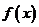 在
在 上是单调函数,求a的取值范围;
上是单调函数,求a的取值范围;
16.(12分)设集合 ,
, .
.
(1)当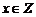 时,求A的非空真子集的个数;
时,求A的非空真子集的个数;
(2)若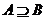 ,求m的取值范围.
,求m的取值范围.
17(12分)已知函数
 ,当
,当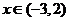 时,
时,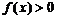 ;当
;当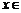 (
(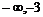 )
) 时,
时,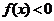 .求
.求 在[m,1]内的值域(其中m为常数);
在[m,1]内的值域(其中m为常数);
18 (12分)盒中装有一打(12个)乒乓球,其中9个新的,3个旧的(用过的球即为旧的),从盒中任取3个使用,用完后装回盒中,此时盒中旧球个数ξ是一个随机变量,求ξ的分布列.
15. 函数 在
在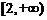 恒正,则实数
恒正,则实数 的范围是
的范围是
三解答题 (共六题,75分)
14.若函数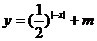 的图象与x轴有公共点,则m的取值范围是
的图象与x轴有公共点,则m的取值范围是
13.二项式(2x3- )7的展开式中常数项是
)7的展开式中常数项是
11.设随机变量X的分布列为 …2010.
…2010.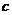 为常数,则
为常数,则
12如果方程x2+2ax+a+1=0的两个根中,一个比2大,另一个比2小,则实数a的取值范围是
9. 已知 ,则
,则 的值等于
.
的值等于
.
10已知函数 满足对任意
满足对任意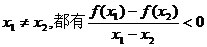 成立,则a的取值范围是
( )
成立,则a的取值范围是
( )
8.偶函数 满足
满足 =
=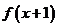 ,且在
,且在 时,
时, ,则关于
,则关于 的方程
的方程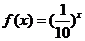 ,在
,在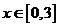 上解的个数是
上解的个数是
A.1 B.2 C.3 D.4
二填空题(每小题5分,共35分)
7..一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则P(ξ=12)等于
A.C (
( )10·(
)10·( )2 B.C
)2 B.C (
( )9(
)9( )2·
)2·
C.C (
( )9·(
)9·( )2 D.C
)2 D.C (
( )9·(
)9·( )2
)2
5.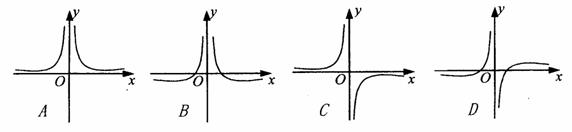 已知曲线
已知曲线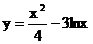 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( )
,则切点的横坐标为( )
(A)3 (B) 2 (C) 1 (D)
6 设函数 区间
区间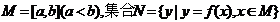 ,则使M=N成立的实数对(a,b),有( )
,则使M=N成立的实数对(a,b),有( )
A.0个 B.1个 C.2个 D.无数多个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com