
9.图中能够说明气候干燥时陆地吸热增温迅速的时段是
A.1月0-6时 B.3月7-12时
C.7月9一15时 D.10月12-18时
图4中①-⑤为0°-66°34′N之间不同日期的昼长分布曲线示意图,读图回答10-11题。
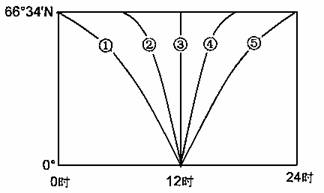
图4
8.如果有同学认为该地气候类型是热带草原气候,他可以从图中找到哪些判断依据
① 终年高温 ② 最高温在4、5月,而不是7月
③ 分干湿两季 ④ 温差较小
A.①②③ B.②③④ C.①③④ D.①②④
7.该地一年中气温日较差最大不超过
A.11℃ B.9℃ C.7℃ D.5℃
6.丙地在城市中
A.为最普遍的类型 B.生态环境最佳
C.交通条件最佳 D.工业点最密集
图3为某地一年中气温日变化的分布图,读图回答7-9题。
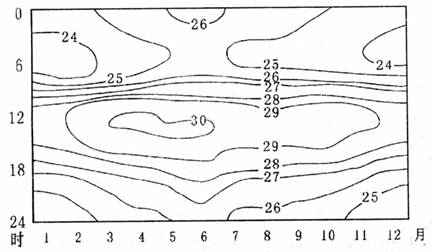
图3
5.乙地土地价格高,人口密度低,应属于
A.中心商务区 B.园林 C.住宅区 D.工业区
4.图示甲地土地价格和人口密度均很低,合理的解释是
A.位于城市中心,为市政中心广场 B.距城市中心近,不利房地产开发
C.位于城市边缘,基础设施不完善 D.位于郊区,只适合电子工业发展
3.若在岛上修建一港口,最适宜的位置是
A.a B.b C.c D.d
图2为印度某城市(由西至东相距25千米)人口密度与土地价格统计,读图回答4-6题。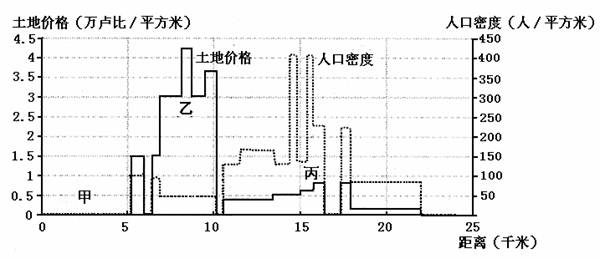
图2
2.关于该岛屿自然地理特征的叙述,正确的是 图1
A.岛上山顶海拔约1680米 B.山顶“天池”是由冰川侵蚀而成
C.该岛属于珊瑚岛 D.附近洋流自西向东流动
1.图中岛屿位于
A.东半球
B.板块消亡边界
C.常绿硬叶林带
D.大西洋
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
复习回顾 整合知识 |
函数的表示法有三种:解析式、图象法、列表法;它们之间可相互转化,常见形式有:解析式 图象法,解析式 图象法,解析式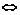 列表法. 列表法. |
师生合作总结上节课的基本知识及基本方法. 重新体会对于特殊函数可进行三种形式之间的互相转化.  师:分析实现不同形式的转化的意义. |
复习回顾、整合知识 |
|
进入课题(求函数解析式) |
例1 (1)已知f (x)是一次函数,且f [f (x)] = 4x – 1,求f (x)及f (2); (2)已知 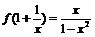 ,求f (x)的解析式; ,求f (x)的解析式; (3)已知 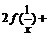 f (x) = x (x≠0),求f (x)的解析式; f (x) = x (x≠0),求f (x)的解析式; (4)已知3f (x5) + f (–x5) = 4x,求f (x)的解析式.                           例2 设f (x)是R上的函数,且满足f (0) = 1,并且对任意实数x,y,有f (x – y) = f (x) – y (2x – y + 1),求f (x)的表达式.      例3 已知f (x)为二次函数,且f (x+1)+f (x–1) = 2x2–4x,  求f (x)的表达式.  小结:求解析式的基本方法:  (1)待定系数法  (2)换元法  (3)配方法 (4)函数方程法. |
学习尝试练习求解,老师指导、点评. 师生合作归纳题型特点及适用方法. 例1解:(1)设f (x) = ax + b (a≠0). 则f [f (x)] = f (ax + b) = a (ax + b) + b = a2x + ab + b. 又f [f (x)] = 4x – 1, ∴a2x + ab + b = 4x – 1. 即 或 ∴f (x) = 2x –,或f (x) = –2x + 1. 则,或f (2) = –3. (2)解法一:∵ == =, ∴f (x) = ==. 解法二:设t = 1+,则. 又, ∴ ==, ∴. (3)令x = a (a≠0),则+ f (a) = a; 令x =(a≠0),则 2 f (a) +. 联立上述两式得f (a) = . ∴f (x) =(x≠0). (4)令x = a,或x = –a,分别可得 解之得f (a5) = 2a. 又令a5 = t, ∴, ∴f (t) = 2, ∴f (x) = 2 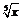 . .例2解:法一:由f (0) = 1,f (x – y) = f (x) – y(2x+y+1). 设x=y,得f (0)= f (x)–x (2x–x+1). ∵f (0) = 1,∴f (x)–x (2x–x+1) = 1, ∴f (x) = x2 + x + 1. 法二:令x = 0,得 f (0–y) = f (0) – y (–y + 1), 即f (–y) = 1 – y (–y + 1). 又令–y = x代入上式得 f (x) = 1– (–x) (x + 1) = 1 + x (x + 1) = x2 + x + 1. 即f (x) = x2 + x + 1. 例3解:设f (x)=ax2+bx+c (a≠0), 则f (x+1) + f (x – 1) = a (x+1)2 + b (x + 1) + c + a (x – 1) + c + a (x – 1)2 + b (x – 1) + c = 2ax2 + 2bx + 2a + 2c = 2x2 – 4x. ∴ 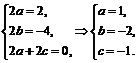 ∴f (x) = x2 – 2x – 1. |
掌握求函数解析式的基本类型及对应方法. |
|
应用举例(函数应用问题) |
例4 用长为l的铁丝变成下部为矩形,上部为半圆形的框架如图所示,若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并指出其定义域. 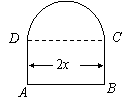  例5 某市“招手即停”公共汽车的票价按下列规则制定: (1)5公里以内(含5公里),票价2元; (2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算). 如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象. 我们把像例4这样的函数称为分段函数.即在函数的定义域内,对于自变量x的值的不同取值区间,有着不同的对应法则,这样的函数通常叫分段函数. 生活中,有很多可以用分段函数描述的实际问题,如出租车的计费、个人所得税纳税额等等. |
师生合作解析例3、例4. 师:反映实际问题的函数定义域怎样确定? 生:解析式有意义和实际问题自身条件确定. 例4解:矩形的长AB = 2x,宽为a,则有2x + 2a + 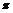 x
= l, x
= l,∴ 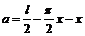 . .半圆的直径为2x,半径为x,所以 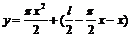 ·2x ·2x = 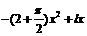 , ,由实际意义得 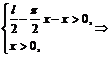 0<x< 0<x<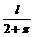 . .即 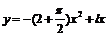 ,定义域为 ,定义域为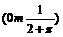 . .例5解:设票价为y,里程为x,由题意可知,自变量x的取值范围是(0, 20]. 由“招手即停”公共汽车票价的制定规则,可得到以下函数解析式: 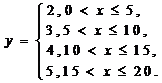 根据这个函数解析式,可画出函数图象,如下图. 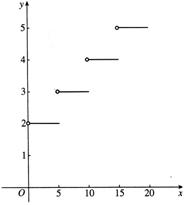 |
培养学生应用数学知识,解决实际问题的能力. |
|
归纳总结 |
1.求函数解析式的方法: 换元法、配方法、待定系数法、赋值法. 2.求实际问题函数解析式,关键找具有因果关系的两个变量的联系式. |
师生合作总结. 学生整理、小结,老师点评、归纳. |
整合知识形成技能. |
|
课后作业 |
1.2
第四课时习案 |
学生独立完成 |
巩固基础、 提高能力 |
备选例题
例1 经市场调查,某商品在近100天内,其销售量和价格均是时间t的函数,且销售量近似地满足关系g (t)
=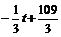 (t∈N*,0<t≤100),在前40天内价格为f (t)
=
(t∈N*,0<t≤100),在前40天内价格为f (t)
=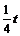 + 22(t∈N*,0≤t≤40),在后60天内价格为
+ 22(t∈N*,0≤t≤40),在后60天内价格为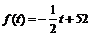 (t∈N*,40<t≤100),求这种商品的日销售额的最大值(近似到1元).
(t∈N*,40<t≤100),求这种商品的日销售额的最大值(近似到1元).
[解析]前40天内日销售额为:
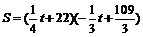 =
=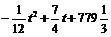
∴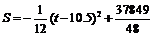
后60天内日销售额为:
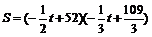 =
=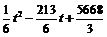 .
.
∴
∴得函数关系式
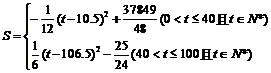
由上式可知:对于0<t≤40且t∈N*,有当t = 10或11时,Smax≈809.
对于40<t≤100且t∈N*,有当t = 41时,Smax = 714.
综上所述得:当t = 10或11时,Smax≈809.
答:第10天或11天日售额最大值为809元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com