
4.了解平面向量基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算.
3.掌握实数与向量的积的运算法则及运算律,理解两个向量共线的充要条件.
2.掌握向量的加法和减法的运算法则及运算律.
1.理解向量的概念,掌握向量的几何表示,了解共线向量的概念.
3.函数的最大值与最小值:
⑴ 设y=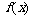 是定义在区间[a ,b ]上的函数,y=
是定义在区间[a ,b ]上的函数,y=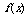 在(a ,b )内有导数,则函数y=
在(a ,b )内有导数,则函数y=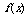 在[a ,b ]上 有最大值与最小值;但在开区间内
有最大值与最小值.
在[a ,b ]上 有最大值与最小值;但在开区间内
有最大值与最小值.
(2) 求最值可分两步进行:
① 求y=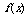 在(a ,b )内的 值;
在(a ,b )内的 值;
② 将y=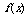 的各 值与
的各 值与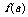 、
、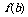 比较,其中最大的一个为最大值,最小的一个为最小值.
比较,其中最大的一个为最大值,最小的一个为最小值.
(3) 若函数y=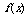 在[a ,b ]上单调递增,则
在[a ,b ]上单调递增,则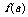 为函数的 ,
为函数的 ,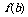 为函数的 ;若函数y=
为函数的 ;若函数y=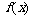 在[a ,b ]上单调递减,则
在[a ,b ]上单调递减,则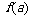 为函数的 ,
为函数的 ,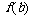 为函数的 .
为函数的 .
|
例1. 已知f(x)=ex-ax-1.
(1)求f(x)的单调增区间;
(2)若f(x)在定义域R内单调递增,求a的取值范围;
(3)是否存在a,使f(x)在(-∞,0]上单调递减,在[0,+∞)上单调递增?若存在,求出a的值;若不存在,说明理由.
解: =ex-a.
=ex-a.
(1)若a≤0, =ex-a≥0恒成立,即f(x)在R上递增.
=ex-a≥0恒成立,即f(x)在R上递增.
若a>0,ex-a≥0,∴ex≥a,x≥lna.∴f(x)的单调递增区间为(lna,+∞).
(2)∵f(x)在R内单调递增,∴ ≥0在R上恒成立.
≥0在R上恒成立.
∴ex-a≥0,即a≤ex在R上恒成立.
∴a≤(ex)min,又∵ex>0,∴a≤0.
(3)方法一 由题意知ex-a≤0在(-∞,0]上恒成立.
∴a≥ex在(-∞,0]上恒成立.∵ex在(-∞,0]上为增函数.
∴x=0时,ex最大为1.∴a≥1.同理可知ex-a≥0在[0,+∞)上恒成立.
∴a≤ex在[0,+∞)上恒成立.∴a≤1,∴a=1.
方法二 由题意知,x=0为f(x)的极小值点.∴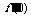 =0,即e0-a=0,∴a=1.
=0,即e0-a=0,∴a=1.
变式训练1. 已知函数f(x)=x3-ax-1.
(1)若f(x)在实数集R上单调递增,求实数a的取值范围;
(2)是否存在实数a,使f(x)在(-1,1)上单调递减?若存在,求出a的取值范围;若不存在,说明理由;
(3)证明:f(x)=x3-ax-1的图象不可能总在直线y=a的上方.
(1)解 由已知 =3x2-a,∵f(x)在(-∞,+∞)上是单调增函数,
=3x2-a,∵f(x)在(-∞,+∞)上是单调增函数,
∴ =3x2-a≥0在(-∞,+∞)上恒成立,即a≤3x2对x∈R恒成立.
=3x2-a≥0在(-∞,+∞)上恒成立,即a≤3x2对x∈R恒成立.
∵3x2≥0,∴只需a≤0,又a=0时, =3x2≥0,
=3x2≥0,
故f(x)=x3-1在R上是增函数,则a≤0.
(2)解 由 =3x2-a≤0在(-1,1)上恒成立,得a≥3x2,x∈(-1,1)恒成立.
=3x2-a≤0在(-1,1)上恒成立,得a≥3x2,x∈(-1,1)恒成立.
∵-1<x<1,∴3x2<3,∴只需a≥3.当a=3时, =3(x2-1),
=3(x2-1),
在x∈(-1,1)上, <0,即f(x)在(-1,1)上为减函数,∴a≥3.
<0,即f(x)在(-1,1)上为减函数,∴a≥3.
故存在实数a≥3,使f(x)在(-1,1)上单调递减.
(3)证明 ∵f(-1)=a-2<a,∴f(x)的图象不可能总在直线y=a的上方.
例2. 已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线为l:3x-y+1=0,若x=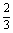 时,y=f(x)有极值.
时,y=f(x)有极值.
(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
解 (1)由f(x)=x3+ax2+bx+c,得 =3x2+2ax+b,
=3x2+2ax+b,
当x=1时,切线l的斜率为3,可得2a+b=0 ①
当x=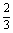 时,y=f(x)有极值,则
时,y=f(x)有极值,则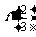 =0,可得4a+3b+4=0
②
=0,可得4a+3b+4=0
②
由①②解得a=2,b=-4.由于切点的横坐标为x=1,∴f(1)=4.
∴1+a+b+c=4.∴c=5.
(2)由(1)可得f(x)=x3+2x2-4x+5,∴ =3x2+4x-4,
=3x2+4x-4,
令 =0,得x=-2,x=
=0,得x=-2,x=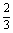 .
.
当x变化时,y,y′的取值及变化如下表:
|
x |
-3 |
(-3,-2) |
-2 |
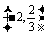 |
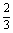 |
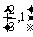 |
1 |
|
y′ |
|
+ |
0 |
- |
0 |
+ |
|
|
y |
8 |
单调递增 ↗ |
13 |
单调递减 ↘ |
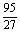 |
单调递增 ↗ |
4 |
∴y=f(x)在[-3,1]上的最大值为13,最小值为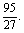
变式训练2. 函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.
解 先求导数,得y′=4x3-4x,令y′=0,即4x3-4x=0.解得x1=-1,x2=0,x3=1.
导数y′的正负以及f(-2),f(2)如下表:
|
x |
-2 |
(-2,-1) |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
(1,2) |
2 |
|
y′ |
|
- |
0 |
+ |
0 |
- |
0 |
+ |
|
|
y |
13 |
↘ |
4 |
↗ |
5 |
↘ |
4 |
↗ |
13 |
从上表知,当x=±2时,函数有最大值13,当x=±1时,函数有最小值4.
例3. 已知函数f(x)=x2e-ax (a>0),求函数在[1,2]上的最大值.
解 ∵f(x)=x2e-ax(a>0),∴ =2xe-ax+x2·(-a)e-ax=e-ax(-ax2+2x).
=2xe-ax+x2·(-a)e-ax=e-ax(-ax2+2x).
令 >0,即e-ax(-ax2+2x)>0,得0<x<
>0,即e-ax(-ax2+2x)>0,得0<x<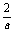 .
.
∴f(x)在(-∞,0),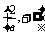 上是减函数,在
上是减函数,在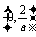 上是增函数.
上是增函数.
①当0<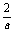 <1,即a>2时,f(x)在(1,2)上是减函数,
<1,即a>2时,f(x)在(1,2)上是减函数,
∴f(x)max=f(1)=e-a.
②当1≤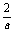 ≤2,即1≤a≤2时,
≤2,即1≤a≤2时,
f(x)在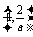 上是增函数,在
上是增函数,在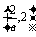 上是减函数,
上是减函数,
∴f(x)max=f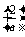 =4a-2e-2.
=4a-2e-2.
③当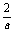 >2时,即0<a<1时,f(x)在(1,2)上是增函数,
>2时,即0<a<1时,f(x)在(1,2)上是增函数,
∴f(x)max=f(2)=4e-2a.
综上所述,当0<a<1时,f(x)的最大值为4e-2a,
当1≤a≤2时,f(x)的最大值为4a-2e-2,
当a>2时,f(x)的最大值为e-a.
变式训练3. 设函数f(x)=-x(x-a)2(x∈R),其中a∈R.
(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)当a≠0时,求函数f(x)的极大值和极小值.
解:(1)当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,
f(2)=-2, =-3x2+4x-1,
=-3x2+4x-1,
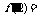 -12+8-1=-5,
-12+8-1=-5,
∴当a=1时,曲线y=f(x)在点(2,f(2))处的切线方程为
5x+y-8=0.
(2)f(x)=-x(x-a)2=-x3+2ax2-a2x,
 =-3x2+4ax-a2=-(3x-a)(x-a),
=-3x2+4ax-a2=-(3x-a)(x-a),
令 =0,解得x=
=0,解得x=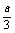 或x=a.
或x=a.
由于a≠0,以下分两种情况讨论.
①若a>0,当x变化时, 的正负如下表:
的正负如下表:
|
x |
(-∞,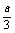 ) ) |
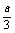 |
(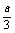 ,a) ,a) |
a |
(a,+∞) |
 |
- |
0 |
+ |
0 |
- |
|
f(x) |
↘ |
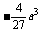 |
↗ |
0 |
↘ |
因此,函数f(x)在x=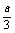 处取得极小值f(
处取得极小值f(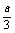 ),
),
且f(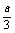 )=-
)=-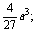
函数f(x)在x=a处取得极大值f(a),且f(a)=0.
②若a<0,当x变化时, 的正负如下表:
的正负如下表:
|
x |
(-∞,a) |
a |
(a,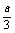 ) ) |
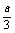 |
(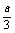 ,+∞) ,+∞) |
 |
- |
0 |
+ |
0 |
- |
|
f(x) |
↘ |
0 |
↗ |
-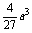 |
↘ |
因此,函数f(x)在x=a处取得极小值f(a),且f(a)=0;
函数f(x)在x=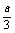 处取得极大值f(
处取得极大值f(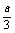 ),
),
且f(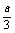 )=-
)=-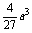 .
.
例4. 某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)2万件. (1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(a).
解 (1)分公司一年的利润L(万元)与售价x的函数关系式为:L=(x-3-a)(12-x)2,x∈[9,11].
(2)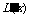 =(12-x)2-2(x-3-a)(12-x)=(12-x)(18+2a-3x).
=(12-x)2-2(x-3-a)(12-x)=(12-x)(18+2a-3x).
令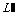 =0得x=6+
=0得x=6+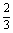 a或x=12(不合题意,舍去).
a或x=12(不合题意,舍去).
∵3≤a≤5,∴8≤6+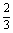 a≤
a≤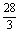 .
.
在x=6+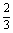 a两侧L′的值由正变负.
a两侧L′的值由正变负.
所以①当8≤6+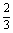 a<9即3≤a<
a<9即3≤a<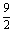 时,Lmax=L(9)=(9-3-a)(12-9)2=9(6-a).
时,Lmax=L(9)=(9-3-a)(12-9)2=9(6-a).
②当9≤6+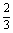 a≤
a≤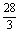 ,即
,即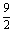 ≤a≤5时,
≤a≤5时,
Lmax=L(6+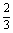 a)=(6+
a)=(6+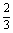 a-3-a)[12-(6+
a-3-a)[12-(6+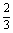 a)]2=4(3-
a)]2=4(3-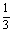 a)3.
a)3.
所以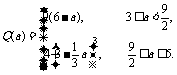
答 若3≤a<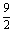 ,则当每件售价为9元时,分公司一年的利润L最大,最大值Q(a)=9(6-a)(万元);若
,则当每件售价为9元时,分公司一年的利润L最大,最大值Q(a)=9(6-a)(万元);若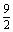 ≤a≤5,则当每件售价为(6+
≤a≤5,则当每件售价为(6+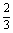 a)元时,分公司一年的利润L最大,最大值Q(a)=
a)元时,分公司一年的利润L最大,最大值Q(a)=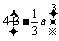 (万元).
(万元).
变式训练4:某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3 700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5 000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).
(1)求利润函数P(x)及边际利润函数MP(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
(3)求边际利润函数MP(x)的单调递减区间,并说明单调递减在本题中的实际意义是什么?
解:(1)P(x)=R(x)-C(x)=-10x3+45x2+3 240x-5 000(x∈N*,且1≤x≤20);
MP(x)=P(x+1)-P(x)=-30x2+60x+3 275 (x∈N*,且1≤x≤19).
(2)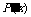 =-30x2+90x+3
240=-30(x-12)(x+9),
=-30x2+90x+3
240=-30(x-12)(x+9),
∵x>0,∴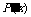 =0时,x=12,
=0时,x=12,
∴当0<x<12时,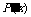 >0,当x>12时,
>0,当x>12时,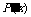 <0,
<0,
∴x=12时,P(x)有最大值.
即年造船量安排12艘时,可使公司造船的年利润最大.
(3)MP(x)=-30x2+60x+3 275=-30(x-1)2+3 305.
所以,当x≥1时,MP(x)单调递减,
所以单调减区间为[1,19],且x∈N*.
MP(x)是减函数的实际意义是:随着产量的增加,每艘利润与前一艘比较,利润在减少.
|
研究可导函数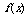 的单调性、极值(最值)时,应先求出函数
的单调性、极值(最值)时,应先求出函数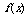 的导函数
的导函数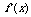 ,再找出
,再找出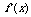 =0的x取值或
=0的x取值或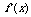 >0(
>0(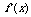 <0)的x的取值范围.
<0)的x的取值范围.
2.可导函数的极值
⑴ 极值的概念
设函数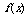 在点
在点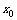 附近有定义,且对
附近有定义,且对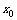 附近的所有点都有 (或 ),则称
附近的所有点都有 (或 ),则称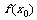 为函数的一个极大(小)值.称
为函数的一个极大(小)值.称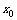 为极大(小)值点.
为极大(小)值点.
⑵ 求可导函数极值的步骤:
① 求导数 ;
;
② 求方程 =0的 ;
=0的 ;
③ 检验 在方程
在方程 =0的根左右的符号,如果在根的左侧附近为正,右侧附近为负,那么函数y=
=0的根左右的符号,如果在根的左侧附近为正,右侧附近为负,那么函数y=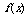 在这个根处取得 ;如果在根的左侧附近为负,右侧为正,那么函数y=
在这个根处取得 ;如果在根的左侧附近为负,右侧为正,那么函数y=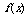 在这个根处取得 .
在这个根处取得 .
1. 函数的单调性
⑴ 函数y=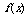 在某个区间内可导,若
在某个区间内可导,若 >0,则
>0,则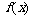 为 ;若
为 ;若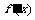 <0,则
<0,则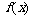 为 .(逆命题不成立)
为 .(逆命题不成立)
(2) 如果在某个区间内恒有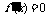 ,则
,则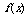 .
.
注:连续函数在开区间和与之相应的闭区间上的单调性是一致的.
(3) 求可导函数单调区间的一般步骤和方法:
① 确定函数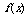 的 ;
的 ;
② 求 ,令 ,解此方程,求出它在定义区间内的一切实根;
,令 ,解此方程,求出它在定义区间内的一切实根;
③ 把函数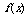 的间断点(即
的间断点(即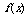 的无定义点)的横坐标和上面的各个实根按由小到大的顺序排列起来,然后用这些点把函数
的无定义点)的横坐标和上面的各个实根按由小到大的顺序排列起来,然后用这些点把函数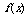 的定义区间分成若干个小区间;
的定义区间分成若干个小区间;
④ 确定 在各小开区间内的 ,根据
在各小开区间内的 ,根据 的符号判定函数
的符号判定函数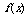 在各个相应小开区间内的增减性.
在各个相应小开区间内的增减性.
3.搞清导数的几何意义,为解决实际问题,如切线、加速度等问题打下理论基础.
第2课时 导数的概念及性质
|
2.要熟记求导公式,对于复合函数的导数要层层求导.
1.理解平均变化率的实际意义和数学意义。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com