
1.认识向量的代数特性.向量的坐标表示,实现了“形”与“数”的互相转化.以向量为工具,几何问题可以代数化,代数问题可以几何化.
4.两个向量 =(x1、y1)和
=(x1、y1)和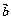 =(x2、y2)共线的充要条件是
.
=(x2、y2)共线的充要条件是
.
|
例1.已知点A(2,3),B(-1,5),且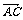 =
=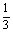
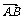 ,求点C的坐标.
,求点C的坐标.
解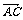 =
=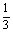
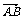 =(-1,
=(-1,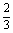 ),
), =
=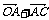 =(1,
=(1, 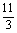 ),即C(1,
),即C(1, 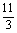 )
)
变式训练1.若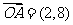 ,
,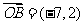 ,则
,则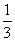
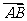 =
.
=
.
解: 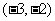 提示:
提示: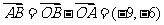
例2. 已知向量 =(cos
=(cos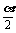 ,sin
,sin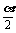 ),
),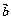 =(cos
=(cos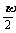 ,sin
,sin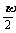 ),|
),| -
-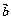 |=
|=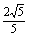 ,求cos(α-β)的值.
,求cos(α-β)的值.
解:| -
-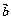 |=
|=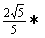
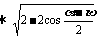 =
=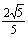
 cos
cos =
=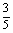
 cos(α-β)=
cos(α-β)=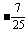
变式训练2.已知 -2
-2 =(-3,1),2
=(-3,1),2 +
+ =(-1,2),求
=(-1,2),求 +
+ .
.
解  =(-1,1),
=(-1,1), =(1,0),∴
=(1,0),∴ +
+ =(0,1)
=(0,1)
例3. 已知向量 =(1, 2),
=(1, 2),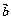 =(x, 1),
=(x, 1),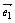 =
= +2
+2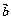 ,
,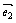 =2
=2 -
-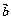 ,且
,且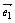 ∥
∥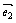 ,求x.
,求x.
解: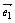 =(1+2x,4),
=(1+2x,4),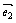 =(2-x,3),
=(2-x,3),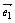 ∥
∥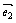
 3(1+2x)=4(2-x)
3(1+2x)=4(2-x) x=
x=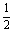
变式训练3.设 =(ksinθ, 1),
=(ksinθ, 1), =(2-cosθ, 1) (0 <θ<π),
=(2-cosθ, 1) (0 <θ<π), ∥
∥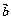 ,求证:k≥
,求证:k≥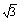 .
.
证明: k=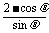 ∴k-
∴k-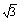 =
=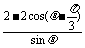 ≥0
∴k≥
≥0
∴k≥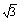
 例4. 在平行四边形ABCD中,A(1,1),
例4. 在平行四边形ABCD中,A(1,1),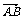 =(6,0),点M是线段AB的中点,线段CM与BD交于点P.
=(6,0),点M是线段AB的中点,线段CM与BD交于点P.
(1) 若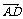 =(3,5),求点C的坐标;
=(3,5),求点C的坐标;
(2) 当|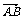 |=|
|=|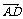 |时,求点P的轨迹.
|时,求点P的轨迹.
解:(1)设点C的坐标为(x0,y0),
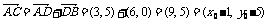
得x0=10 y0=6 即点C(10,6)
(2) ∵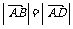 ∴点D的轨迹为(x-1)2+(y-1)2=36 (y≠1)
∴点D的轨迹为(x-1)2+(y-1)2=36 (y≠1)
∵M为AB的中点 ∴P分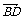 的比为
的比为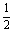
设P(x,y),由B(7,1) 则D(3x-14,3y-2)
∴点P的轨迹方程为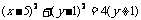
变式训练4.在直角坐标系x、y中,已知点A(0,1)和点B(-3,4),若点C在∠AOB的平分线上,且| |=2,求
|=2,求 的坐标.
的坐标.
解 已知A (0,1),B (-3,4) 设C (0,5),
D (-3,9)
则四边形OBDC为菱形 ∴∠AOB的角平分线是菱形OBDC的对角线OD
∵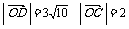
∴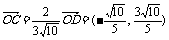
|
3.平面向量的坐标运算:
若 =(x1、y1),
=(x1、y1),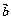 =(x2、y2),λ∈R,则:
=(x2、y2),λ∈R,则:
 +
+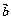 =
=
 -
-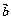 =
=
λ =
=
已知A(x1、y1),B(x2、y2),则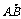 =
.
=
.
2.向量的坐标表示与起点为 的向量是一一对应的关系.
1.平面向量的坐标表示
分别取与x轴、y轴方向相同的两个单位向量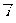 、
、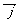 作为基底,对于一个向量
作为基底,对于一个向量 ,有且只有一对实数x、y,使得
,有且只有一对实数x、y,使得 =x
=x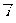 +y
+y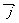 .我们把(x、y)叫做向量
.我们把(x、y)叫做向量 的直角坐标,记作 .并且|
的直角坐标,记作 .并且| |= .
|= .
4.向量加法的三角形法则可以推广为多个向量求和的多边形法则,特点:首尾相接首尾连;向量减法的三角形法则特点:首首相接连终点.
第2课时 平面向量的坐标运算
|
3.注意平行向量与平行线段的区别.用向量方法证明AB∥CD,需证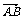 ∥
∥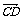 ,且AB与CD不共线.要证A、B、C三点共线,则证
,且AB与CD不共线.要证A、B、C三点共线,则证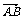 ∥
∥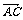 即可.
即可.
2.注意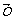 与O的区别.零向量与任一向量平行.
与O的区别.零向量与任一向量平行.
1.认识向量的几何特性.对于向量问题一定要结合图形进行研究.向量方法可以解决几何中的证明.
4.⑴ 平面向量基本定理:如果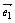 、
、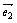 是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量
是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 ,有且只有一对实数
,有且只有一对实数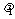 、
、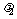 ,使得 .
,使得 .
⑵ 设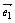 、
、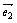 是一组基底,
是一组基底, =
=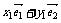 ,
,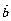 =
=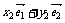 ,则
,则 与
与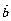 共线的充要条件是 .
共线的充要条件是 .
|
例1.已知△ABC中,D为BC的中点,E为AD的中点.设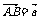 ,
,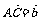 ,求
,求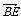 .
.
解: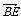 =
=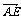 -
-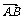 =
=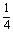 (
(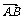 +
+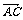 )-
)-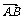 =-
=-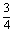
 +
+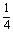
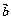
变式训练1.如图所示,D是△ABC边AB上的中点,则向量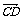 等于( )
等于( )
 A.-
A.-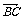 +
+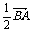
B.-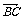 -
-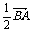
C.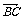 -
-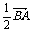
D.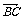 +
+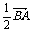
解:A
例2. 已知向量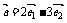 ,
,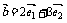 ,
,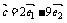 ,其中
,其中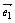 、
、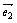 不共线,求实数
不共线,求实数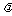 、
、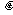 ,使
,使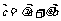 .
.
解: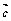 =λ
=λ +μ
+μ
 2
2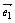 -9
-9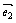 =(2λ+2μ)
=(2λ+2μ)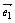 +(-3λ+3μ)
+(-3λ+3μ)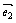
 2λ+2μ=2,且-3λ+3μ=-9
2λ+2μ=2,且-3λ+3μ=-9 λ=2,且μ=-1
λ=2,且μ=-1
变式训练2:已知平行四边形ABCD的对角线相交于O点,点P为平面上任意一点,求证: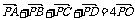
证明 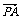 +
+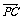 =2
=2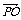 ,
,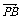 +
+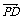 =2
=2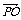

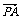 +
+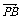 +
+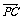 +
+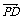 =4
=4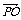
例3. 已知ABCD是一个梯形,AB、CD是梯形的两底边,且AB=2CD,M、N分别是DC和AB的中点,若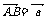 ,
,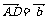 ,试用
,试用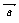 、
、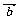 表示
表示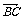 和
和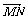 .
.
解:连NC,则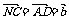
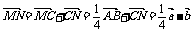 ;
;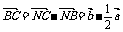
 变式训练3:如图所示,OADB是以向量
变式训练3:如图所示,OADB是以向量 =
= ,
,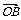 =
=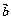 为邻边的平行四边形,又
为邻边的平行四边形,又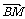 =
=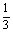
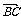 ,
,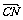 =
=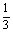
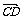 ,试用
,试用 、
、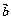 表示
表示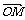 ,
,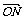 ,
,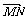 .
.
解: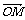 =
=
 +
+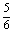
 ,
,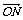 =
=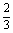
 +
+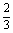
 ,
,
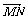 =
=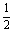
 -
-

例4. 设 ,
,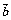 是两个不共线向量,若
是两个不共线向量,若 与
与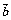 起点相同,t∈R,t为何值时,
起点相同,t∈R,t为何值时, ,t
,t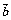 ,
,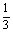 (
( +
+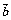 )三向量的终点在一条直线上?
)三向量的终点在一条直线上?
解:设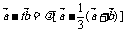 (
(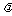 ∈R)化简整理得:
∈R)化简整理得: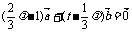
∵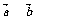 ,∴
,∴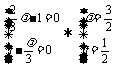
故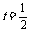 时,
时,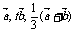 三向量的向量的终点在一直线上.
三向量的向量的终点在一直线上.
变式训练4:已知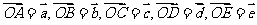 ,设
,设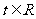 ,如果
,如果
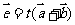 ,那么
,那么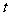 为何值时,
为何值时,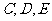 三点在一条直线上?
三点在一条直线上?
解:由题设知,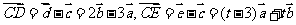 ,
,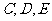 三点在一条
三点在一条
直线上的充要条件是存在实数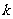 ,使得
,使得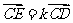 ,即
,即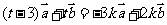 ,
,
整理得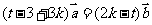 .
.
①若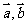 共线,则
共线,则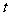 可为任意实数;
可为任意实数;
②若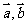 不共线,则有
不共线,则有 ,解之得,
,解之得,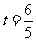 .
.
综上,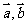 共线时,则
共线时,则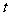 可为任意实数;
可为任意实数;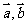 不共线时,
不共线时,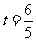 .
.
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com