
1.了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发现中的作用。
3.应根据定义找两个向量的夹角。对于不共起点的两个向量,通过平移,使起点重合.
2.注意 ·
· 与ab的区别.
与ab的区别. ·
· =0≠>
=0≠> =
=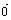 ,或
,或 =
=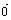 .
.
1.运用向量的数量积可以解决有关长度、角度等问题.因此充分挖掘题目所包含的几何意义,往往能得出巧妙的解法.
5.向量数量积的运算律:
⑴  ·
· = ;
= ;
⑵ (λ )·
)· = =
= = ·(λ
·(λ )
)
⑶ ( +
+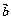 )·
)·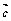 =
=
|
例1. 已知| |=4,|
|=4,| |=5,且
|=5,且 与
与 的夹角为60°,求:(2
的夹角为60°,求:(2 +3
+3 )·(3
)·(3 -2
-2 ).
).
解:(2 +3
+3 )(3
)(3 -2
-2 )=-4
)=-4
变式训练1.已知| |=3,|
|=3,| |=4,|
|=4,| +
+ |=5,求|2
|=5,求|2 -3
-3 |的值.
|的值.
解: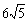
例2. 已知向量 =(sin
=(sin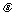 ,1),
,1), =(1,cos
=(1,cos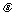 ),-
),-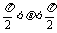 .
.
(1) 若a⊥b,求 ;
;
(2) 求| +
+ |的最大值.
|的最大值.
解:(1)若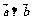 ,则
,则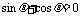
即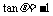 而
而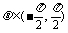 ,所以
,所以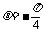
(2)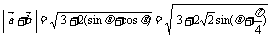
当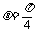 时,
时,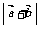 的最大值为
的最大值为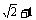
变式训练2:已知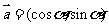 ,
,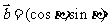 ,其中
,其中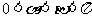 .
(1)求证:
.
(1)求证: 与
与 互相垂直;
(2)若
互相垂直;
(2)若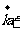
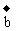 与
与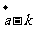
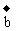 的长度相等,求
的长度相等,求 的值(
的值(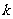 为非零的常数).
为非零的常数).
证明: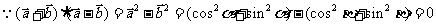
 与
与 互相垂直
互相垂直
(2)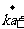
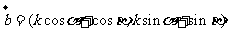 ,
,
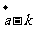
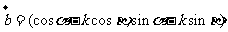 ,
,
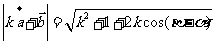 ,
,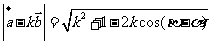 ,
,
而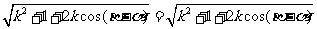
 ,
,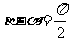
例3. 已知O是△ABC所在平面内一点,且满足(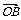 -
-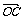 )·(
)·(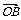 +
+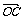 -2
-2 )=0,判断△ABC是哪类三角形.
)=0,判断△ABC是哪类三角形.
解:设BC的中点为D,则(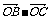 )(
)(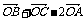 )=0
)=0 2
2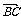 ·
·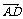 =0
=0 BC⊥AD
BC⊥AD △ABC是等腰三角形.
△ABC是等腰三角形.
变式训练3:若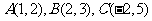 ,则△ABC的形状是
.
,则△ABC的形状是
.
解: 直角三角形.提示: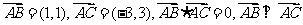
例4. 已知向量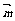 =(cosθ, sinθ)和
=(cosθ, sinθ)和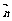 =(
=(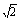 -sinθ, cosθ) θ∈(π, 2π)且|
-sinθ, cosθ) θ∈(π, 2π)且|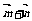 |=
|=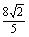 ,求cos(
,求cos(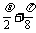 )的值.
)的值.
解: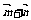 =(cosθ-sinθ+
=(cosθ-sinθ+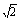 , cosθ+sinθ)由已知(cosθ-sinθ+
, cosθ+sinθ)由已知(cosθ-sinθ+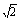 )2+(cosθ+sinθ)2=
)2+(cosθ+sinθ)2=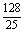
化简:cos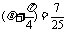
又cos2
∵θ∈(π,
2π) ∴cos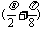 <0
<0
∴cos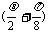 =-
=-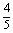
变式训练4.平面向量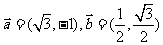 ,若存在不同时为
,若存在不同时为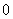 的实数
的实数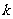 和
和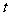 ,使
,使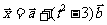 ,
, 且
且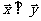 ,试求函数关系式
,试求函数关系式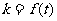 .
.
解:由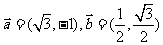 得
得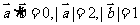
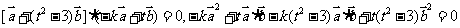
|
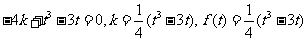
4.向量数量积的性质:设 、
、 都是非零向量,
都是非零向量,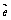 是单位向量,θ是
是单位向量,θ是 与
与 的夹角.
的夹角.
⑴ 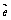 ·
· =
= ·
·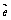 =
=
⑵  ⊥
⊥
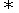
⑶ 当 与
与 同向时,
同向时, ·
· = ;当
= ;当 与
与 反向时,
反向时, ·
· = .
= .
⑷ cosθ= .
⑸ | ·
· |≤
|≤
3.向量的数量积的几何意义:
| |cosθ叫做向量
|cosθ叫做向量 在
在 方向上的投影 (θ是向量
方向上的投影 (θ是向量 与
与 的夹角).
的夹角).
 ·
· 的几何意义是,数量
的几何意义是,数量 ·
· 等于
.
等于
.
2.两个向量的数量积的定义:已知两个非零向量 与
与 ,它们的夹角为θ,则数量
叫做
,它们的夹角为θ,则数量
叫做 与
与 的数量积(或内积),记作
的数量积(或内积),记作 ·
· ,即
,即 ·
· =
.规定零向量与任一向量的数量积为0.若
=
.规定零向量与任一向量的数量积为0.若 =(x1, y1),
=(x1, y1), =(x2, y2),则
=(x2, y2),则 ·
· =
.
=
.
1.两个向量的夹角:已知两个非零向量 和
和 ,过O点作
,过O点作 =
= ,
,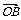 =
= ,则∠AOB=θ (0°≤θ≤180°) 叫做向量
,则∠AOB=θ (0°≤θ≤180°) 叫做向量 与
与 的 .当θ=0°时,
的 .当θ=0°时, 与
与 ;当θ=180°时,
;当θ=180°时, 与
与 ;如果
;如果 与
与 的夹角是90°,我们说
的夹角是90°,我们说 与
与 垂直,记作
.
垂直,记作
.
2.由于向量有几何法和坐标法两种表示方法,所以我们应根据题目的特点去选择向量的表示方法,由于坐标运算方便,可操作性强,因此应优先选用向量的坐标运算.
第3课时 平面向量的数量积
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com