
3.理解组合的意义,掌握组合数计算公式和组合数性质,并能用它们解决一些简单的应用问题.
2.理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题.
1.掌握分类计数原理与分步计数原理、并能用它分析和解决一些简单的应用问题.
3.实际问题中有关术语、名称.
(1)仰角和俯角:在目标视线和水平视线所成的角中,目标视线在水平视线上方的角叫仰角;在水平视线下方的角叫俯角
(2)方位角:指正北方向顺时针转到目标方向线水平角.
|
例1.(1)某人朝正东方走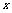 km后,向左转1500,然后朝新方向走3km,结果它离出发点恰好
km后,向左转1500,然后朝新方向走3km,结果它离出发点恰好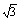 km,那么
km,那么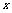 等于
( )
等于
( )
(A)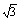 (B)
(B)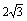 (C)
(C)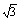 或
或 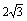 (D)3
(D)3
解:C 提示:利用余弦定理
(2)甲、乙两楼相距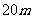 ,从乙楼底望甲楼顶的仰角为
,从乙楼底望甲楼顶的仰角为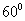 ,从甲楼顶望乙楼顶的俯角为
,从甲楼顶望乙楼顶的俯角为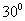 ,则甲、乙两楼的高分别是 ( )
,则甲、乙两楼的高分别是 ( )
A
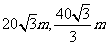 B
B 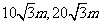
C
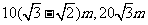 D
D 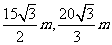
解:A
(3)一只汽球在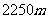 的高空飞行,汽球上的工件人员测得前方一座山顶上A点处的俯角为
的高空飞行,汽球上的工件人员测得前方一座山顶上A点处的俯角为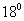 ,汽球向前飞行了
,汽球向前飞行了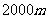 后,又测得A点处的俯角为
后,又测得A点处的俯角为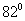 ,则山的高度为( )
,则山的高度为( )
A
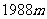 B
B 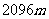 C
C 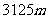 D
D 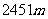
解: B
(4)已知轮船A和轮船B同时离开C岛,A向北偏东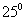 方向,B向西偏北
方向,B向西偏北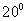 方向,若A的航行速度为25 nmi/h,B的速度是A的
方向,若A的航行速度为25 nmi/h,B的速度是A的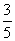 ,过三小时后,A、B的距离是 .
,过三小时后,A、B的距离是 .
解:90.8 nmi
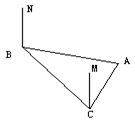 (5) 货轮在海上以40km/h的速度由B到C航行,
(5) 货轮在海上以40km/h的速度由B到C航行,
航向为方位角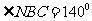 ,A处有灯塔,
,A处有灯塔,
其方位角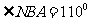 ,在C处观测灯塔A的
,在C处观测灯塔A的
方位角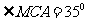 ,由B到C需航行半小时,
,由B到C需航行半小时,
则C到灯塔A的距离是
解: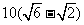 km 提示:由题意知
km 提示:由题意知 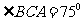 ,利用余弦定理或解直角三角形可得
,利用余弦定理或解直角三角形可得
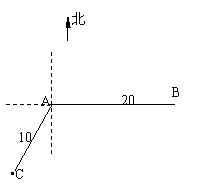
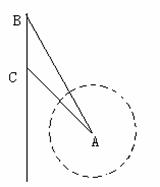
变式训练1:如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30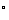 ,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1
,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1 )?
)?
 解:连接BC,由余弦定理得BC2=202+102-2×20×10×cos120°=700.
解:连接BC,由余弦定理得BC2=202+102-2×20×10×cos120°=700.
于是,BC=10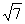 .
.
∵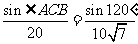 , ∴sin∠ACB=
, ∴sin∠ACB=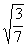 ,
,
∵∠ACB<90° ∴∠ACB=41°
∴乙船应朝北偏东71°方向沿直线前往B处救援.
例2. 在某海滨城市附近海面有一台风,据检测,当前台风中心位于城市O(如图)的东偏南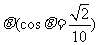 方向300
km的海面P处,并以20
km /
h的速度向西偏北
方向300
km的海面P处,并以20
km /
h的速度向西偏北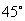 的方向移动,台风侵袭的范围为圆形区域,当前半径为60
km ,并以10
km /
h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?
的方向移动,台风侵袭的范围为圆形区域,当前半径为60
km ,并以10
km /
h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?
解:设在时刻t(h)台风中心为Q,此时台风侵袭的圆形区域半径为10t+60(km)
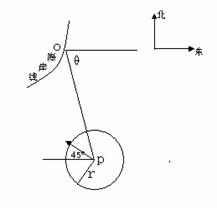 若在时刻t城市O受到台风的侵袭,则
若在时刻t城市O受到台风的侵袭,则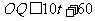
由余弦定理知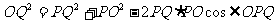
由于PO=300,PQ=20t
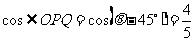
故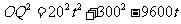
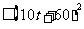
即 解得
解得 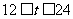
答:12小时后该城市受到台风的侵袭,侵袭的时间将持续12小时.
变式训练2:如图所示,海岛A周围38海里内有暗礁,一艘船向正南方向航行,在B处测得岛A在船的南偏东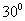 方向上,船航行30海里后,在C处测得岛A在船的南偏东
方向上,船航行30海里后,在C处测得岛A在船的南偏东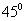 方向上,如果此船不改变航向,继续向南航行,有无触礁危险?
方向上,如果此船不改变航向,继续向南航行,有无触礁危险?
 解:由题意得,在△ABC中,BC=30,
解:由题意得,在△ABC中,BC=30,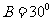 ,
,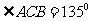
所以 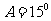 ,由正弦定理可知:
,由正弦定理可知: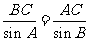
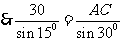 所以
所以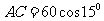 ,
,
于是A到BC所在直线的距离为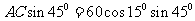
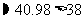
所以船继续向南航行无触礁危险。
例3. 如图所示,公园内有一块边长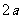 的等边△ABC形状的三角地,
的等边△ABC形状的三角地,
现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,
E在AC上.
(1)设AD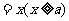 ,ED
,ED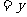 ,求用
,求用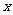 表示
表示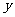 的函数关系式;
的函数关系式;
(2)如果DE是灌溉水管,为节约成本希望它最短,DE的位置
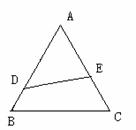 应该在哪里?如果DE是参观线路,则希望它最长,DE的
应该在哪里?如果DE是参观线路,则希望它最长,DE的
位置又在哪里?请给予证明.
解:(1)在△ABC中,D在AB上,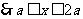
 S△ADE=
S△ADE=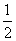 S△ABC
S△ABC 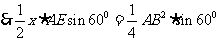
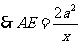 ,在△ADE中,由余弦定理得:
,在△ADE中,由余弦定理得:
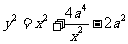
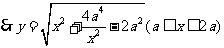
(2)令 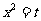 ,则
,则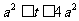 则
则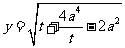
令 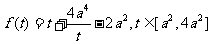 ,
,
则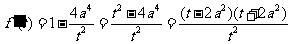
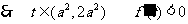 ;
;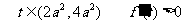
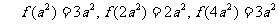
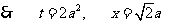
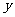 有最小值
有最小值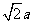 ,此时DE∥BC,且
,此时DE∥BC,且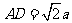
 有最大值
有最大值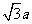 ,此时DE为△ABC
,此时DE为△ABC
的边AB或AC的中线上.
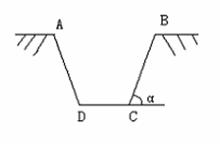
变式训练3:水渠道断面为等腰梯形,如图所示,渠道深为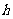 ,梯形面积为S,为了使渠道的渗水量达到最小,应使梯形两腰及下底之和达到最小,此时下底角
,梯形面积为S,为了使渠道的渗水量达到最小,应使梯形两腰及下底之和达到最小,此时下底角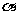 应该是多少?
应该是多少?
 解:设
解:设 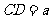 ,则
,则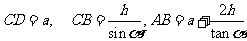 ,
,
所以 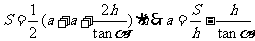
设两腰与下底之和为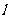 ,
,
则
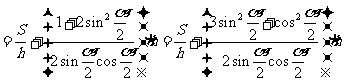
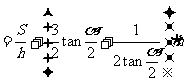
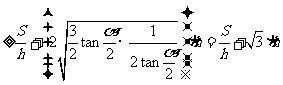
当且仅当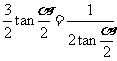 时,上式取等号,即当
时,上式取等号,即当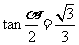 时,上式取等号
时,上式取等号
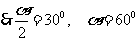 ,所以下角
,所以下角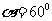 时,梯形两腰及下底之和达到最小.
时,梯形两腰及下底之和达到最小.
例4. 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC。问:点B在什么位置时,四边形OACB面积最大?
解:设 ,在△AOB中,由余弦定理得:
,在△AOB中,由余弦定理得:
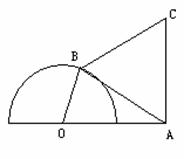
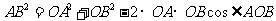
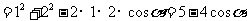
于是,四边形OACB的面积为
S=S△AOB+ S△ABC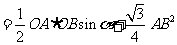
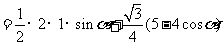
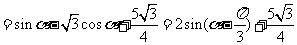
因为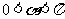 ,所以当
,所以当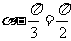 ,
,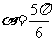 ,即
,即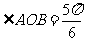 时,
时,
四边形OACB面积最大.
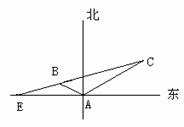 变式训练4:如图所示,某海岛上一观察哨A上午11时测得一轮船在海岛北偏东
变式训练4:如图所示,某海岛上一观察哨A上午11时测得一轮船在海岛北偏东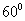 的C处,12时20分测得船在海岛北偏西
的C处,12时20分测得船在海岛北偏西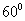 的B处,12时40分轮船到达位于海岛正西方且距海岛5 km的E港口,如果轮船始终匀速直线前进,问船速多少?
的B处,12时40分轮船到达位于海岛正西方且距海岛5 km的E港口,如果轮船始终匀速直线前进,问船速多少?
解:轮船从C到B用时80分钟,从B到E用时20分钟,
而船始终匀速前进,由此可见:BC=4EB,设EB=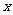 ,则
,则
则BC=4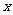 ,由已知得
,由已知得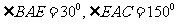
在△AEC中,由正弦定理得:
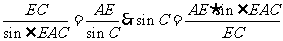
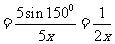
在△ABC中,由正弦定理得: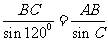
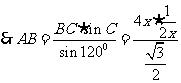
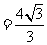
在△ABE中,由余弦定理得: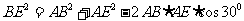
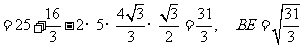
所以船速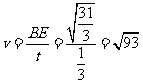 答:该船的速度为
答:该船的速度为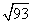 km/h
km/h
2.正弦定理和余弦定理解三角形的常见问题有:测量距离问题、测量高度问题、测量角度问题、计算面积问题、航海问题、物理问题等;
1.三角形中的有关公式(正弦定理、余弦定理、三角形内角和定理、三角形面积公式等);
3.对于与测量和与几何计算有关的实际问题,可以考虑转化为解三角形的问题.
|
2.三角形中含边角的恒等变形问题,通常是运用正弦定理或余弦定理,要么将其变为含边的代数式做下去,要么将其变为含角的三角式做下去,请合理选择.
1.已知两边和其中一边的对角求其他的边和角,这种题型可能无解、一解、两解等,要特别注意.
3.三角形的面积公式:
|
例1. 在△ABC中,已知a=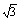 ,b=
,b=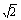 ,B=45°,求角A、C及边c.
,B=45°,求角A、C及边c.
解 A1=60° C1=75° c1=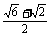
A2=120° C2=15° c2=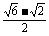
变式训练1:(1)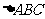 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且
的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且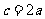 ,则
,则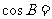 ( )
( )
A.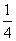 B.
B.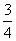 C.
C.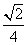 D.
D.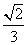
解:B 提示:利用余弦定理
(2)在△ABC中,由已知条件解三角形,其中有两解的是 ( )
A.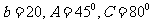 B.
B.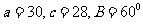
C.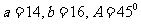 D.
D.
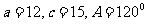
解:C 提示:在斜三角形中,用正弦定理求角时,若已知小角求大角,则有两解;若已知大角求小角,则只有一解
(3)在△ABC中,已知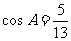 ,
,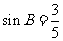 ,则
,则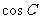 的值为( )
的值为( )
A 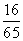 B
B 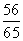 C
C 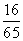 或
或 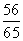 D
D 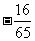
解:A 提示:在△ABC中,由 知角B为锐角
知角B为锐角
(4)若钝角三角形三边长为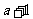 、
、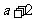 、
、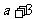 ,则
,则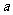 的取值范围是 .
的取值范围是 .
解: 提示:由
提示:由 可得
可得
(5)在△ABC中,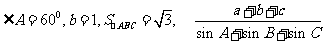 = .
= .
解: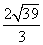 提示:由面积公式可求得
提示:由面积公式可求得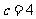 ,由余弦定理可求得
,由余弦定理可求得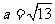
例2. 在△ABC中,若 sinA=2sinB cos C, sin2A=sin2B+sin2C,试判断△ABC的形状.
解:sinA=2sinBcosC
 sin(B+C)=2sinBcosC
sin(B+C)=2sinBcosC
 sin(B-C)=0
sin(B-C)=0 B=C
B=C
sin2A=sin2B+sin2C a2=b2+c2
a2=b2+c2
 ∠A=90°
∠A=90°
∴ △ABC是等腰直角三角形。
变式训练2:在△ABC中,sinA=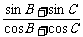 ,判断这个三角形的形状.
,判断这个三角形的形状.
解:应用正弦定理、余弦定理,可得
a=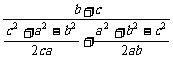 ,所以b(a2-b2)+c(a2-c2)=bc(b+c).所以(b+c)a2=(b3+c3)+bc(b+c).所以a2=b2-bc+c2+bc.所以a2=b2+c2.所以△ABC是直角三角形.
,所以b(a2-b2)+c(a2-c2)=bc(b+c).所以(b+c)a2=(b3+c3)+bc(b+c).所以a2=b2-bc+c2+bc.所以a2=b2+c2.所以△ABC是直角三角形.
例3. 已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C.
解:由sinA(sinB+cosB)-sinC=0,得sinAsinB+sinAcosB-sin(A+B)=0,
所以sinB(sinA-cosA)=0
∵B∈(0, π), ∴sinB≠0, ∴cosA=sinA,由A∈(0, π),知A=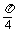 从而B+C=
从而B+C=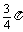 ,由sinB+cos2C=0得sinB+cos2(
,由sinB+cos2C=0得sinB+cos2(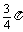 -B)=0
-B)=0
cos=(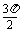 -2B)=cos[2π-(
-2B)=cos[2π-(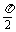 +2B)]=cos(
+2B)]=cos(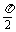 +2B)=-sin2B
+2B)=-sin2B
得sinB-sin2B=0,亦即sinB-2sinBcosB=0,由此各cosB=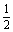 ,B=
,B=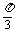 ,C=
,C=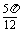
∴A=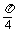 B=
B=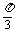 C=
C=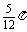
变式训练3:已知△ABC中,2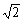 (sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为
(sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为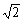 .
.
(1)求∠C;
(2)求△ABC面积的最大值.
解:(1)由2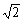 (sin2A-sin2C)=(a-b)·sinB得
(sin2A-sin2C)=(a-b)·sinB得
2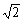 (
(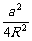 -
-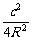 )=(a-b)
)=(a-b)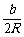 .
.
又∵R=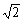 ,∴a2-c2=ab-b2.∴a2+b2-c2=ab.∴cosC=
,∴a2-c2=ab-b2.∴a2+b2-c2=ab.∴cosC=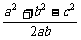 =
=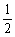 .
.
又∵0°<C<180°,∴C=60°.
(2)S=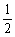 absinC=
absinC=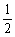 ×
×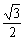 ab=2
ab=2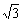 sinAsinB=2
sinAsinB=2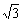 sinAsin(120°-A)
sinAsin(120°-A)
=2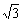 sinA(sin120°cosA-cos120°sinA)=3sinAcosA+
sinA(sin120°cosA-cos120°sinA)=3sinAcosA+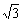 sin2A
sin2A
=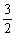 sin2A-
sin2A-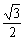 cos2A+
cos2A+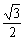 =
=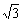 sin(2A-30°)+
sin(2A-30°)+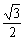 .
.
∴当2A=120°,即A=60°时,Smax=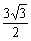 .
.
例4. 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G.设∠MGA=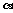 (
(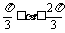 ).
).
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为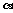 的函数;
的函数;
(2)求y=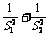 的最大值与最小值.
的最大值与最小值.
解 (1) AG=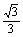 ,∠
,∠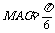
由正弦定理得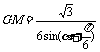 ,
,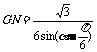
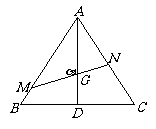
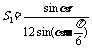 ,
,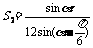
(2)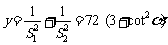
∵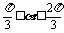 ∴当
∴当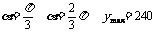
当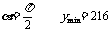
变式训练4:在在△ABC中,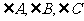 所对的边分别为
所对的边分别为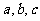 ,,且
,,且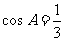
(1)求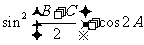 的值;
的值;
(2)若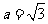 ,求
,求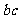 的最大值;
的最大值;
解:(1)因为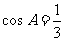 ,故
,故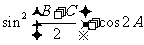
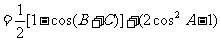
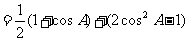
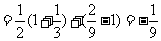
(2)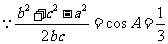
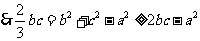
又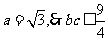 ,当且仅当
,当且仅当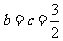 时,
时,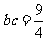
故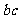 的最大值是
的最大值是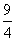
|
|||
|
|||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com