
1、设A={a,b},集合B={a+1,5},若A∩B={2},则A∪B= ( )
A.{1,2} B.{1,5} C.{2,5} D.{1,2,5}
10.已知函数f(x)=(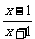 )2(x>1).
)2(x>1).
(1)求f(x)的反函数f-1(x);
(2)判定f-1(x)在其定义域内的单调性;
(3)若不等式(1-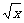 )f-1(x)>a(a-
)f-1(x)>a(a-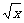 )对x∈[
)对x∈[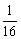 ,
,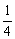 ]恒成立,求实数a的取值范围.
]恒成立,求实数a的取值范围.
解:(1)由y=(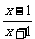 )2,得x=
)2,得x=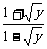 .
.
又y=(1-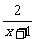 )2,且x>1,∴0<y<1.
)2,且x>1,∴0<y<1.
∴f-1(x)=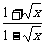 (0<x<1).
(0<x<1).
(2)设0<x1<x2<1,则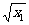 -
-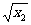 <0,1-
<0,1-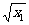 >0,1-
>0,1-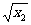 >0.
>0.
∴f-1(x1)-f-1(x2)=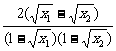 <0,即f-1(x1)<f-1(x2).
<0,即f-1(x1)<f-1(x2).
∴f-1(x)在(0,1)上是增函数.
(3)由题设有(1-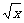 )
)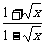 >a(a-
>a(a-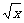 ).
).
∴1+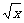 >a2-a
>a2-a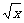 ,即(1+a)
,即(1+a)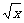 +1-a2>0对x∈[
+1-a2>0对x∈[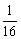 ,
,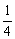 ]恒成立.显然a≠-1.令t=
]恒成立.显然a≠-1.令t=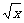 ,∵x∈[
,∵x∈[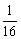 ,
,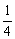 ],∴t∈[
],∴t∈[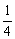 ,
,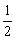 ]则g(t)=(1+a)t+1-a2>0对t∈[
]则g(t)=(1+a)t+1-a2>0对t∈[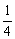 ,
,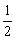 ]恒成立.
]恒成立.
由于g(t)=(1+a)t+1-a2是关于t的一次函数,∴g(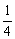 )>0且g(
)>0且g(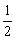 )>0,即
)>0,即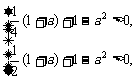 解得-1<a<
解得-1<a<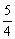 .
.
10、已知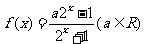 ,是
,是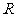 上的奇函数
上的奇函数
(1)求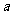 的值,
的值,
(2)求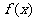 的反函数,
的反函数,
(3)对任意的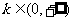 解不等式
解不等式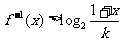

解:(1)由题知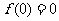 ,得
,得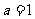 ,此时
,此时
 ,
,
即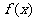 为奇函数
为奇函数
(2)∵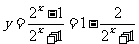 ,得
,得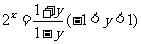 ,
,
∴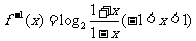

(3)∵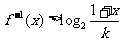 ,
,
∴ ,∴
,∴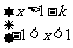 ,
,
①当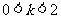 时,原不等式的解集
时,原不等式的解集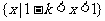 ,
,
②当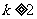 时,原不等式的解集
时,原不等式的解集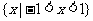

[探索题]
9、已知函数f(x)=a+bx-1(b>0,b≠1)的图象经过点(1,3),函数f-1(x+a)(a>0)的图象经过点(4,2),试求函数f-1(x)的表达式.
解:∵函数f(x)=a+bx-1(b>0,b≠1)的图象经过点(1,3),∴a+b0=3,a=3-b0=
3-1=2.又函数f-1(x+a)(a>0)的图象经过点(4,2),∴f-1(4+a)=2.
∴f(2)=4+a=4+2=6,即2+b2-1=6.∴b=4.
故f(x)=2+4x-1.再求其反函数即得
f-1(x)=log4(x-2)+1(x>2).
8、设函数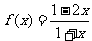 ,又函数
,又函数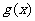 与
与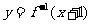 的图象关于
的图象关于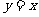 对称,求
对称,求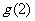 的值
的值
解法一:由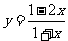 得
得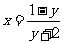 ,∴
,∴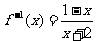 ,
,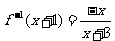 ,
,
∴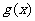 与
与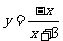 互为反函数,由
互为反函数,由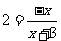 ,得
,得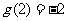

解法二:由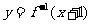 得
得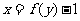 ,∴
,∴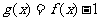 ,
,
∴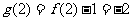

7、 求函数f(x)=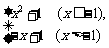 的反函数.
的反函数.
解:当x≤-1时,y=x2+1≥2,且有x=-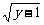 ,此时反函数为y=-
,此时反函数为y=-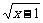 (x≥2).
(x≥2).
当x>-1时,y=-x+1<2,且有x=-y+1,此时反函数为y=-x+1(x<2).
∴f(x)的反函数f-1(x)=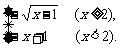
点评:分段函数应在各自的条件下分别求反函数式及反函数的定义域,分段函数的反函数也是分段函数.
6、由y-1=f(2x-1) 得2x-1=f -1(y-1), 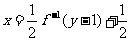 ,互换x,y即得反函数。
,互换x,y即得反函数。
[解答题]
6、已知函数y=f(x)的反函数为y=f-1(x),函数y=f(2x-1)+1的反函数为
简答:1-3:AAB;
4、a=1;5、2;6、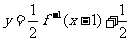
提示:4、点(0,1)在原函数图象上,则(1,0)也在原函数图象上,代入得a=1;
5、已知函数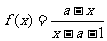 ,其反函数
,其反函数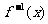 的图象的对称中心是
的图象的对称中心是 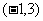 , 则实数
, 则实数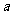 =
=
4、若函数y=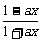 (x≠-
(x≠-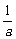 ,x∈R)的图象关于直线y=x对称,则a的值为______.
,x∈R)的图象关于直线y=x对称,则a的值为______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com