
20、已知函数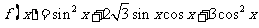 .
.
(Ⅰ)求函数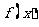 的单调增区间;
的单调增区间;
(Ⅱ)已知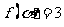 ,且
,且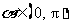 ,求α的值.
,求α的值.
[解](Ⅰ)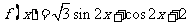 =
=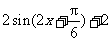
由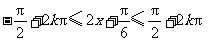 ,得
,得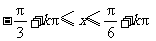 .
.
∴函数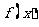 的单调增区间为
的单调增区间为 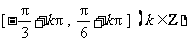
(Ⅱ)由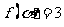 ,得
,得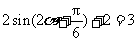 .
.
∴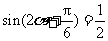 .
.
∴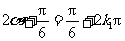 ,或
,或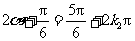
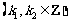 ,
,
即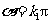 或
或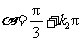
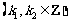 .
.
∵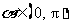 ,∴
,∴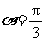 .
.
19、已知等差数列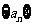 满足
满足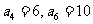 .
.
(1)求数列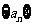 的通项公式;
的通项公式;
(2)设等比数列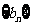 各项均为正数,其前
各项均为正数,其前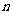 项和
项和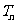 ,若
,若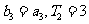 ,求
,求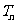 .
.
18、已知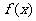 =
=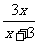 ,数列{
,数列{ }满足
}满足 =
=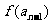
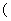
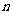 >1,
>1,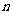 ∈N
∈N ,
,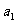 ≠0
≠0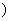 .
.
(1)求证:{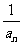 }是等差数列;
(2)若
}是等差数列;
(2)若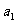 =
=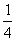 ,求
,求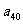 的值.
的值.
解:(1)由 =
=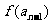 ,得:
,得: =
=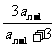 ,
,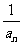 =
=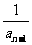 +
+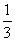
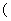
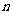 >1,
>1,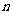 ∈N
∈N
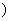
∴数列{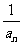 }是以
}是以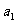 为首项,以
为首项,以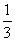 为公差的等差数列.
为公差的等差数列.
(2)∵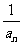 =
=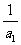 +
+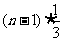 =
=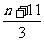 ,∴
,∴ =
=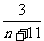 ,
,
得: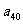 =
=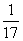 .
.
17、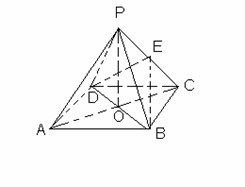 如图,ABCD是正方形,O是正方形的中心,PO
如图,ABCD是正方形,O是正方形的中心,PO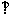 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE ;
(2)平面PAC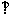 平面BDE.
平面BDE.
16、已知数列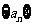 满足
满足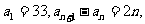 则
则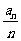 的最小值为__________.
的最小值为__________.
15、若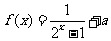 是奇函数,则
是奇函数,则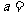
14、若以连续掷两次骰子分别得点数m,n作为点P的横、纵坐标,则点P落在圆x2+y2=16内的概率是 .
13、等差数列{an}、{bn}的前n项和分别为Sn和Tn,若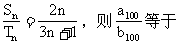
12、某学生家长为缴纳该学生上大学时的教育费,于2003年8月20号从银行贷款a元,为还清这笔贷款,该家长从2004年起每年的8月20号便去银行偿还确定的金额,计划恰好在贷款的m年后还清,若银行按年利息为p的复利计息(复利:即将一年后的贷款利息也纳入本金计算新的利息),则该学生家长每年的偿还金额是 ( )
A.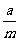 B.
B.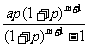 C.
C.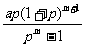 D.
D.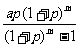
11、把函数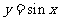 (
(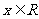 )的图象上所有点向左平行移动
)的图象上所有点向左平行移动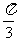 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的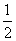 倍(纵坐标不变),得到的图象所表示的函数是( )
倍(纵坐标不变),得到的图象所表示的函数是( )
(A)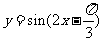 ,
, (B)
(B)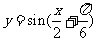 ,
,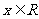
(C)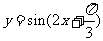 ,
,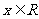 (D)
(D)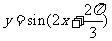 ,
,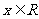
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com