
4.(人教A版选修1-1,2-1第47页习题2.1B组第3题)
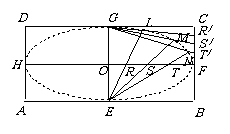 如图,矩形ABCD中,
如图,矩形ABCD中,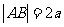 ,
,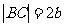 ,E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,
,E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,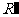 ,
, ,
, 是线段CF的四等分点.请证明直线ER与
是线段CF的四等分点.请证明直线ER与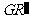 、ES与
、ES与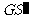 、ET与
、ET与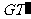 的交点L,M,N在同一个椭圆上.
的交点L,M,N在同一个椭圆上.
变式1:直线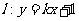 与双曲线
与双曲线 的右支交于不同的两点A、B.若双曲线C的右焦点F在以AB为直径的圆上时,则实数
的右支交于不同的两点A、B.若双曲线C的右焦点F在以AB为直径的圆上时,则实数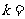 .
.
解:将直线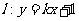 代入双曲线C的方程
代入双曲线C的方程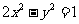 整理,得
整理,得
 ……①
……①
依题意,直线L与双曲线C的右支交于不同两点,故
 解得
解得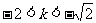 .
.
设A、B两点的坐标分别为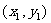 、
、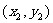 ,则由①式得
,则由①式得
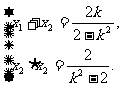 ……②
……②
∵双曲线C的右焦点F 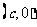 在以AB为直径的圆上,则由FA⊥FB得:
在以AB为直径的圆上,则由FA⊥FB得:

整理,得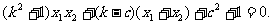 ……③
……③
把②式及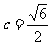 代入③式化简,得
代入③式化简,得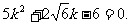
解得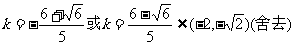 ,故
,故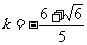 .
.
变式2(2002年广东卷):A、B是双曲线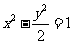 上的两点,点N(1,2)是线段AB的中点.
上的两点,点N(1,2)是线段AB的中点.
(Ⅰ)求直线AB的方程;
(Ⅱ)如果线段AB的垂直平分线与双曲线相交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
解:(Ⅰ)直线AB的方程为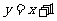 .(求解过程略)
.(求解过程略)
(Ⅱ)联立方程组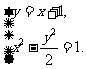 得
得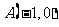 、
、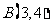 .
.
由CD垂直平分AB,得CD方程为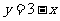 .
.
代入双曲线方程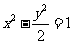 整理,得
整理,得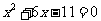 .
.
记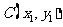 ,
,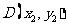 以及CD的中点为
以及CD的中点为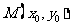 ,
,
则有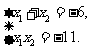 从而
从而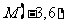 .
.
∵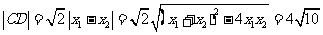 .
.
∴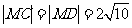 .
.
又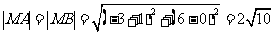 .
.
即A、B、C、D四点到点M的距离相等.
故A、B、C、D四点共圆.
变式3(2005年湖北卷):设A、B是椭圆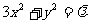 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定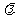 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的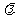 ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
(Ⅰ)解法1:依题意,可设直线AB的方程为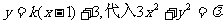 整理,得
整理,得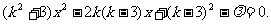 ①
①
设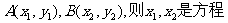 ①的两个不同的根,
①的两个不同的根,
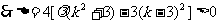 ②
②
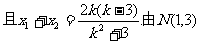 是线段AB的中点,得
是线段AB的中点,得
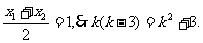
解得 =-1,代入②得,
=-1,代入②得, >12,即
>12,即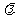 的取值范围是(12,+
的取值范围是(12,+ ).
).
于是,直线AB的方程为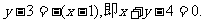
解法2:设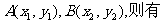
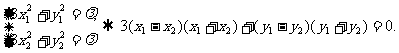
依题意,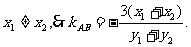

(Ⅱ)解法1: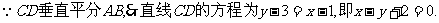 代入椭圆方程,整理得
代入椭圆方程,整理得
 ③
③
 ③的两根,
③的两根,
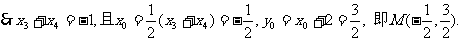
于是由弦长公式可得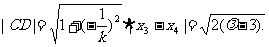 ④
④
将直线AB的方程
 ⑤
⑤
同理可得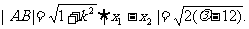 ⑥
⑥
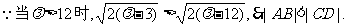
假设在在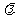 >12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.点M到直线AB的距离为
>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.点M到直线AB的距离为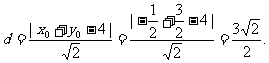 ⑦
⑦
于是,由④、⑥、⑦式和勾股定理可得
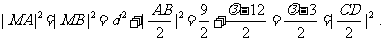
故当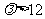 时,A、B、C、D四点均在以M为圆心,
时,A、B、C、D四点均在以M为圆心,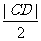 为半径的圆上.
为半径的圆上.
(注:上述解法中最后一步可按如下解法获得:
A、B、C、D共圆 △ACD为直角三角形,A为直角
△ACD为直角三角形,A为直角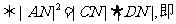
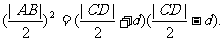 ⑧
⑧
由⑥式知,⑧式左边=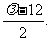
由④和⑦知,⑧式右边=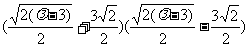
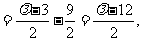
∴⑧式成立,即A、B、C、D四点共圆
解法2:由(Ⅱ)解法1及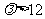 .
.
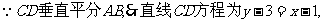 代入椭圆方程,整理得
代入椭圆方程,整理得
 ③ 解得
③ 解得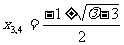 .
.
将直线AB的方程 代入椭圆方程,整理得
代入椭圆方程,整理得
 ⑤ 解得
⑤ 解得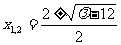 .
.
不妨设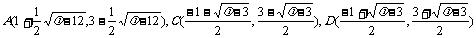
∴
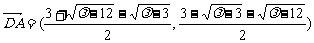
计算可得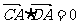 ,∴A在以CD为直径的圆上.
,∴A在以CD为直径的圆上.
又点A与B关于CD对称,∴A、B、C、D四点共圆.
(注:也可用勾股定理证明AC⊥AD)
3.(人教A版选修1-1,2-1第47页习题2.1A组第6题)
已知点P是椭圆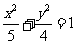 上的一点,且以点P及焦点
上的一点,且以点P及焦点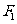 ,
,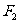 为顶点的三角形的面积等于1,求点P的坐标.
为顶点的三角形的面积等于1,求点P的坐标.
变式1(2004年湖北卷理):已知椭圆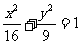 的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为
的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为
A. B.3 C.
B.3 C.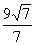 D.
D.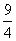
解:依题意,可知当以F1或F2为三角形的直角顶点时,点P的坐标为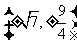 ,则点P到x轴的距离为
,则点P到x轴的距离为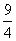 ,故选D.(可以证明不存在以点P为直角顶点的三角形)
,故选D.(可以证明不存在以点P为直角顶点的三角形)
变式2(2006年全国卷Ⅱ):已知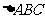 的顶点B、C在椭圆
的顶点B、C在椭圆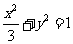 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则 的周长是
的周长是
A. B.6 C.
B.6 C.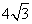 D.12
D.12
解:由于椭圆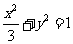 的长半轴长
的长半轴长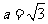 ,而根据椭圆的定义可知
,而根据椭圆的定义可知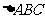 的周长为
的周长为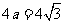 ,故选C.
,故选C.
2.(人教A版选修1-1,2-1第40页练习第3题)
已知经过椭圆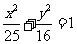 的右焦点
的右焦点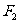 作垂直于x轴的直线A
B,交椭圆于A,B两点,
作垂直于x轴的直线A
B,交椭圆于A,B两点,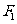 是椭圆的左焦点.
是椭圆的左焦点.
(1)求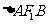 的周长;
的周长;
(2)如果AB不垂直于x轴,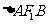 的周长有变化吗?为什么?
的周长有变化吗?为什么?
变式1(2005年全国卷Ⅲ):设椭圆的两个焦点分别为F1、、F2,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率是
A.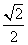 B.
B.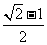 C.
C.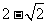 D.
D.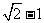
解一:设椭圆方程为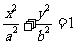 ,依题意,显然有
,依题意,显然有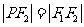 ,则
,则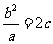 ,即
,即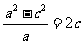 ,即
,即 ,解得
,解得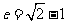 .选D.
.选D.
解二:∵△F1PF2为等腰直角三角形,∴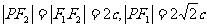 .
.
∵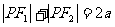 ,∴
,∴ ,∴
,∴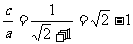 .故选D.
.故选D.
变式2:已知双曲线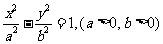 的左,右焦点分别为
的左,右焦点分别为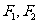 ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且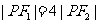 ,则此双曲线的离心率e的最大值为
.
,则此双曲线的离心率e的最大值为
.
解一:由定义知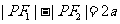 ,又已知
,又已知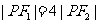 ,解得
,解得 ,
,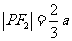 ,在
,在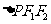 中,由余弦定理,得
中,由余弦定理,得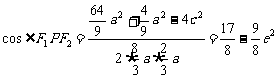 ,要求
,要求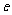 的最大值,即求
的最大值,即求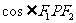 的最小值,当
的最小值,当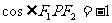 时,解得
时,解得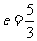 .即
.即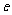 的最大值为
的最大值为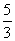 .
.
解二:设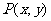 ,由焦半径公式得
,由焦半径公式得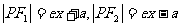 ,∵
,∵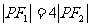 ,∴
,∴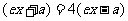 ,∴
,∴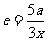 ,∵
,∵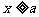 ,∴
,∴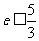 ,∴
,∴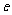 的最大值为
的最大值为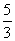 .
.
变式3(2005年全国卷Ⅰ):已知椭圆的中心为坐标原点O,焦点在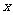 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,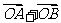 与
与 共线.
共线.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且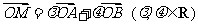 ,证明
,证明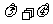 为定值.
为定值.
解:(Ⅰ)设椭圆方程为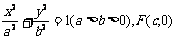 ,
,
则直线AB的方程为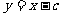 ,代入
,代入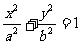 ,化简得
,化简得
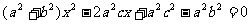 .
.
设A(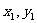 ),B
),B ),则
),则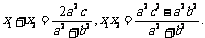
由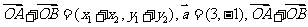 与
与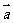 共线,得
共线,得
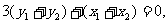 又
又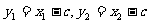 ,
,
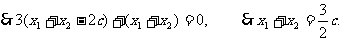
即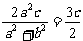 ,所以
,所以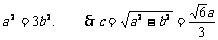 ,
,
故离心率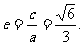
(Ⅱ)证明:由(Ⅰ)知 ,所以椭圆
,所以椭圆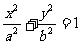 可化为
可化为
设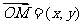 ,由已知得
,由已知得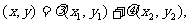
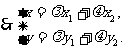
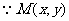 在椭圆上,
在椭圆上,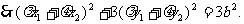
即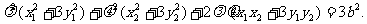 ①
①
由(Ⅰ)知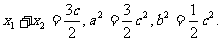


又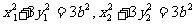 ,代入①得
,代入①得
故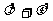 为定值,定值为1.
为定值,定值为1.
命题人:广州市教育局教研室 曾辛金
1. (人教A版选修1-1,2-1第39页例2)
(人教A版选修1-1,2-1第39页例2)
如图,在圆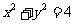 上任取一点P,过点P作X轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?
上任取一点P,过点P作X轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?
变式1:设点P是圆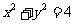 上的任一点,定点D的坐标为(8,0).当点P在圆上运动时,求线段PD的中点M的轨迹方程.
上的任一点,定点D的坐标为(8,0).当点P在圆上运动时,求线段PD的中点M的轨迹方程.
解:设点M的坐标为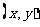 ,点P的坐标为
,点P的坐标为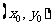 ,则
,则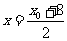 ,
,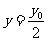 .即
.即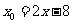 ,
,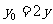 .
.
因为点P 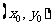 在圆
在圆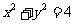 上,所以
上,所以
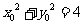 .
.
即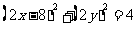 ,
,
即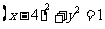 ,这就是动点M的轨迹方程.
,这就是动点M的轨迹方程.
变式2:设点P是圆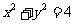 上的任一点,定点D的坐标为(8,0),若点M满足
上的任一点,定点D的坐标为(8,0),若点M满足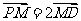 .当点P在圆上运动时,求点M的轨迹方程.
.当点P在圆上运动时,求点M的轨迹方程.
解:设点M的坐标为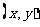 ,点P的坐标为
,点P的坐标为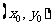 ,由
,由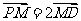 ,得
,得
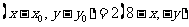 ,
,
即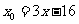 ,
,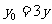 .
.
因为点P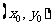 在圆
在圆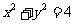 上,所以
上,所以
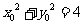 .
.
即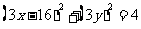 ,
,
即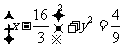 ,这就是动点M的轨迹方程.
,这就是动点M的轨迹方程.
变式3:设点P是曲线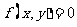 上的任一点,定点D的坐标为
上的任一点,定点D的坐标为 ,若点M满足
,若点M满足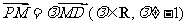 .当点P在曲线
.当点P在曲线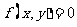 上运动时,求点M的轨迹方程.
上运动时,求点M的轨迹方程.
解:设点M的坐标为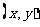 ,点P的坐标为
,点P的坐标为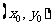 ,由
,由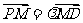 ,得
,得
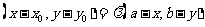 ,
,
即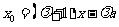 ,
,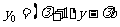 .
.
因为点P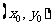 在圆
在圆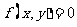 上,所以
上,所以
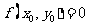 .
.
即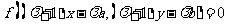 ,这就是动点M的轨迹方程.
,这就是动点M的轨迹方程.
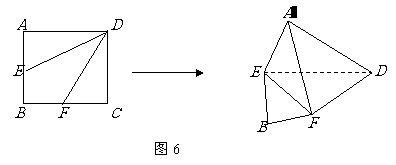
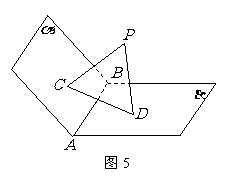
6.(人教A版,必修2,P87,B组第1题)
如图5,边长为2的正方形ABCD中,
(1)点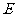 是
是 的中点,点
的中点,点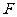 是
是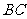 的中点,将
的中点,将 分别沿
分别沿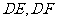 折起,使
折起,使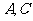 两点重合于点
两点重合于点 ,求证:
,求证: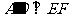 .
.
(2)当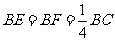 时,求三棱锥
时,求三棱锥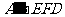 的体积.
的体积.

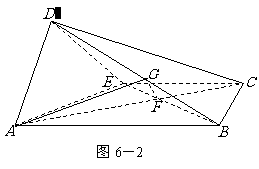
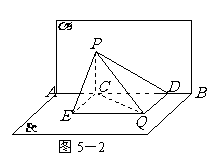
变式题.如图5-1,在矩形 中,
中, 是
是 的中点,以
的中点,以 为折痕将
为折痕将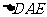 向上折起,使
向上折起,使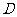 为
为 ,且平面
,且平面 平面
平面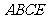 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求直线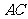 与平面
与平面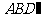 所成角的正弦值.
所成角的正弦值.
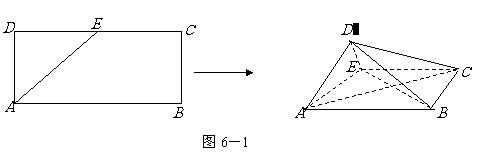

解(Ⅰ)在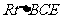 中,
中, ,
,
在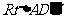 中,
中, ,
,
∵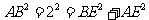 ,
,
∴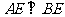 .
.
∵平面 平面
平面 ,且交线为
,且交线为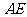 ,
,
∴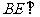 平面
平面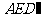 .
.
∵ 平面
平面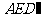 ,
,
∴ .
.
(Ⅱ)设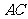 与
与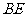 相交于点
相交于点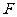 ,由(Ⅰ)知
,由(Ⅰ)知 ,
,
∵ ,
,
∴ 平面
平面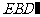 ,
,
∵ 平面
平面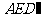 ,
,
∴平面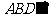 平面
平面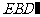 ,且交线为
,且交线为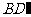 ,
,
如图6-2,作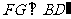 ,垂足为
,垂足为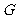 ,则
,则 平面
平面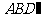 ,
,
连结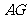 ,则
,则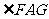 是直线
是直线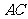 与平面
与平面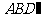 所成的角.
所成的角.
由平面几何的知识可知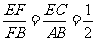 ,∴
,∴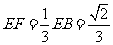 .
.
在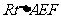 中,
中,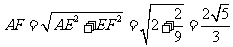 ,
,
在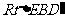 中,
中,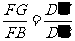 ,可求得
,可求得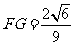 .
.
∴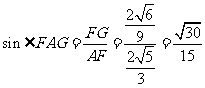 .
.
∴直线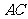 与平面
与平面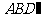 所成的角的正弦值为
所成的角的正弦值为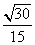 .
.
5.(人教A版,必修2,P87,第10题)
如图5,已知平面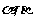 ,且
,且 是垂足,试判断直线
是垂足,试判断直线 与
与 的位置关系?并证明你的结论.
的位置关系?并证明你的结论.
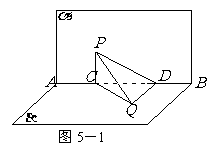 变式题5-1,如图5,已知平面
变式题5-1,如图5,已知平面 ,且
,且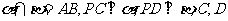 是垂足.
是垂足.
(Ⅰ)求证: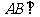 平面
平面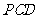 ;
;
(Ⅱ)若 ,试判断平面
,试判断平面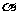 与平面
与平面 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
变式题5-1,如图5,已知平面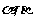 ,
,
且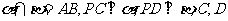 是垂足.
是垂足.
(Ⅰ)求证: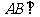 平面
平面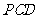 ;
;
(Ⅱ)若 ,试判断平面
,试判断平面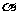 与平面
与平面 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
解(Ⅰ)因为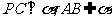 ,所以
,所以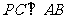 .同理
.同理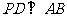 .
.
又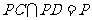 ,故
,故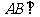 平面
平面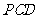 .
.
(Ⅱ)设 与平面
与平面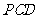 的交点为
的交点为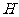 ,连结
,连结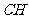 、
、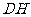 .
.
因为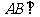 平面
平面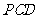 ,所以
,所以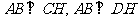 ,
,
所以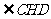 是二面角
是二面角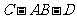 的平面角.
的平面角.
又 ,所以
,所以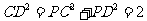 ,即
,即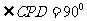 .
.
在平面四边形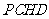 中,
中,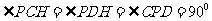 ,
,
所以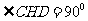 .
.
故平面 平面
平面 .
.
 变式题5-2.如图5-1,已知直二面角
变式题5-2.如图5-1,已知直二面角 ,
,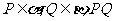 与平面
与平面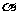 、
、 所成的角都为
所成的角都为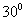 ,
,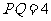 .
.
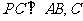 为垂足,
为垂足,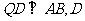 为垂足.
为垂足.
(Ⅰ)求直线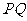 与
与 所成角的大小;
所成角的大小;
(Ⅱ)求四面体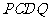 的体积.
的体积.
解:(Ⅰ)如图5-2,在平面 内,作
内,作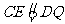 ,连结
,连结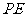 、
、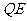 .则四边形
.则四边形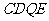 为平行四边形,所以
为平行四边形,所以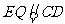 ,即
,即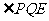 为直线
为直线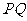 与
与 所成的角(或其补角).
所成的角(或其补角).
因为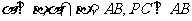 .
.
所以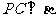 .同理
.同理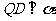 .
.
又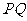 与平面
与平面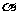 、
、 所成角为
所成角为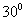 ,所以
,所以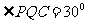 ,
,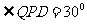 ,所以
,所以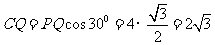 ,
,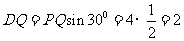 .
.
在 中,
中,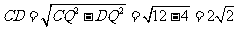 ,从而
,从而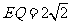 .
.
因为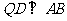 ,且
,且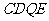 为平行四边形,
为平行四边形,
所以 .
.
又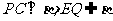 ,所以
,所以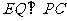 .
.
故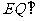 平面
平面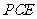 ,从而
,从而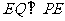 .
.
在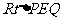 中,
中,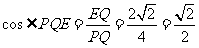 .
.
所以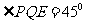 ,
,
即直线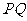 与
与 所成角的大小为
所成角的大小为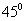 .
.
(Ⅱ)在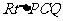 中,
中, ,所以
,所以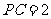 .
.
三角形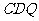 的面积
的面积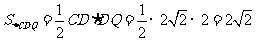 ,
,
故四面体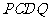 的体积
的体积
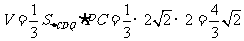 .
.
4.(人教A版,必修2,P74.例2)
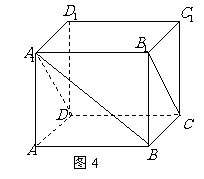 如图4,在正方体
如图4,在正方体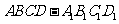 中,求直线
中,求直线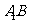 与平面
与平面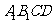 所成的角.
所成的角.
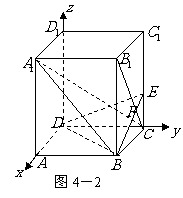
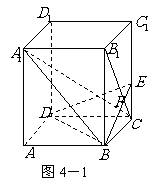 变式题:如图4-1,已知正四棱柱
变式题:如图4-1,已知正四棱柱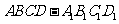 中,底面边长
中,底面边长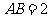 ,侧棱
,侧棱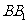 的长为4,过点
的长为4,过点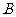 作
作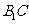 的的垂线交侧棱
的的垂线交侧棱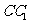 于点
于点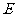 ,交
,交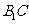 于点
于点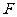 .
.
(Ⅰ)求证: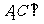 平面
平面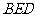 ;
;
(Ⅱ)求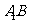 与平面
与平面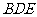 所成的角的正弦值.
所成的角的正弦值.
解:(Ⅰ)如图4-2,以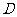 为原点,
为原点,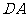 、
、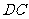 、
、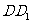 所在直线分别为
所在直线分别为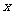 、
、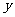 、
、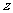 轴建立空间直角坐标系
轴建立空间直角坐标系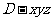 .
.
∴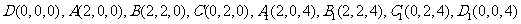 .
.
设 ,则
,则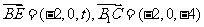 .
.
 ∵
∵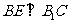 ,∴
,∴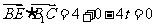 .
.
∴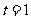 ,∴
,∴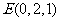 ,
,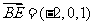 .
.
又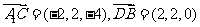 ,
,
∴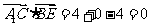 且
且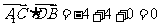 .
.
∴ 且
且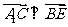 .
.
∴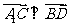 且
且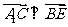 .∴
.∴ 平面
平面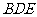 .
.
(Ⅱ)由(Ⅰ)知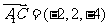 是平面
是平面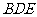 的一个法向量,又
的一个法向量,又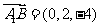 ,
,
∴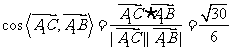 .
.
∴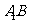 与平面
与平面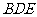 所成角的正弦值为
所成角的正弦值为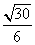 .
.
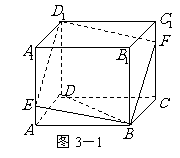
3.(北师大版.必修2.P31.第4题)
如图3,已知E,F分别是正方体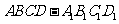 的棱
的棱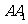 和棱
和棱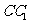 上的点,且
上的点,且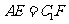 ,求证:四边形
,求证:四边形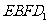 是平行四边形
是平行四边形

变式题:如图3-1.已知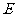 、
、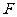 分别是正方体
分别是正方体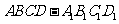 的棱
的棱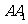 和棱
和棱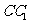 的中点.
的中点.
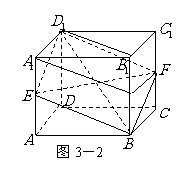 (Ⅰ)试判断四边形
(Ⅰ)试判断四边形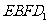 的形状;
的形状;
(Ⅱ)求证:平面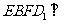 平面
平面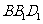 .
.
解(Ⅰ)如图3-2,取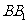 的中点
的中点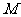 ,连结
,连结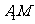 、
、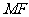 .
.
∵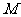 、
、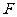 分别是
分别是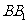 和
和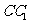 的中点,
的中点,
 ∴
∴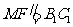 ,
,
在正方体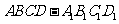 中,有
中,有
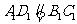 , ∴
, ∴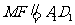 ,
,
∴四边形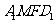 是平行四边形,
是平行四边形,
∴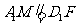 .
.
又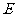 、
、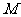 分别是
分别是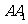 、
、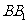 的中点,
的中点,
∴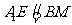 ,
,
∴四边形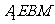 为平行四边形,
为平行四边形,
∴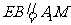 .
.
故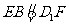 .
.
∴四边形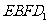 是平行四边形.
是平行四边形.
又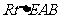 ≌
≌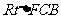 ,
,
∴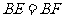 ,
,
故四边形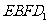 为菱形.
为菱形.
(Ⅱ)连结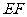 、
、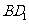 、
、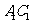 . ∵四边形
. ∵四边形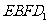 为菱形,
为菱形,
∴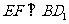 .
.
在正方体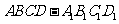 中,有
中,有
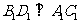 ,
,
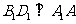
∴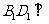 平面
平面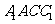 .
.
又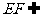 平面
平面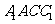 ,
,
∴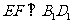 .
.
又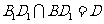 ,
,
∴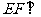 平面
平面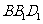 .
.
又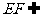 平面
平面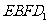 ,
,
故平面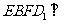 平面
平面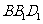
2.(人教A版,必修2,P20.例3)
如图2,已知几何体的三视图,用斜二测画法画出它的直观图.
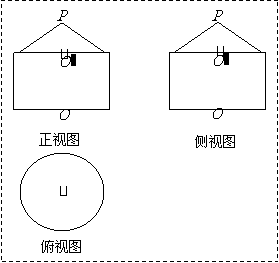
变式题2-1.如图2-1.已知几何体的三视图(单位:cm).
(Ⅰ)画出它的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积和体积.
|
解(Ⅰ)这个几何体的直观图如图2-2所示.
(Ⅱ)这个几何体是一个简单组合体,它的下部是一个圆柱(底面半径为1cm,高为2cm),它的上部是一个圆锥(底面半径为1cm,母线长为2cm,高为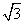 cm).
cm).
所以所求表面积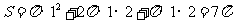
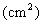 ,
,
 所求体积
所求体积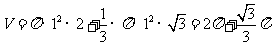
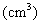 .
.
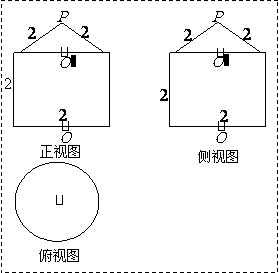
变式题2-2.如图2-3,已知几何体的三视图(单位:cm).
(Ⅰ)画出这个几何体的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积及体积;
(Ⅲ)设异面直线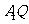 、
、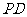 所成角为
所成角为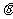 ,求
,求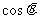 .(理科考生)
.(理科考生)


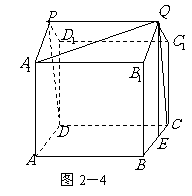
解:(Ⅰ)这个几何体的直观图如图2-4所示.
(Ⅱ)这个几何体可看成是由正方体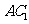 及直三棱柱
及直三棱柱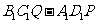 的组合体.
的组合体.
 由
由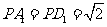 ,
,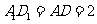 ,
,
可得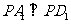 .
.
故所求几何体的全面积
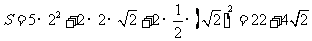
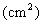
所求几何体的体积
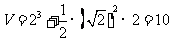
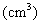
(Ⅲ)由 ,且
,且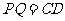 ,可知
,可知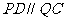 ,
,
故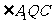 为异面直线
为异面直线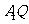 、
、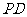 所成的角(或其补角).
所成的角(或其补角).
由题设知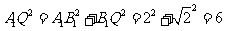 ,
,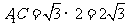 ,
,
取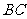 中点
中点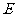 ,则
,则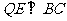 ,且
,且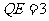 ,
,
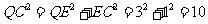 .
.
由余弦定理,得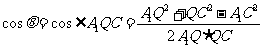
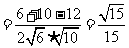 .
.
命题人:黄埔区教育局教研室 肖凌戆. 2007.5
1.(人教A版,必修2.P17.第4题)
图1是一个几何体的三视图,想象它的几何结构特征,并说出它的名称.


变式题1.如图1-1是一个几何体的三视图(单位:cm)
(Ⅰ)画出这个几何体的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积及体积;
(Ⅲ)设异面直线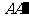 与
与 所成的角为
所成的角为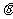 ,求
,求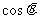 .
.
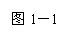
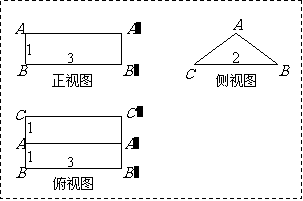
解:(Ⅰ)这个几何体的直观图如图1-2所示.
(Ⅱ)这个几何体是直三棱柱.
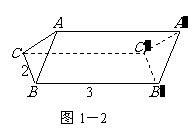 由于底面
由于底面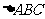 的高为1,所以
的高为1,所以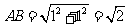 .
.
故所求全面积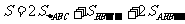

 .
.
这个几何体的体积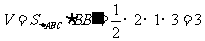
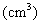
(Ⅲ)因为 ,所以
,所以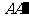 与
与 所成的角是
所成的角是 .
.
在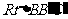 中,
中, ,
,
故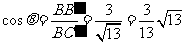 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com