
4、(江苏版第62页习题7)(1)已知数列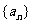 的通项公式为
的通项公式为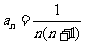 ,求前
,求前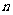 项的和;(2)已知数列
项的和;(2)已知数列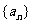 的通项公式为
的通项公式为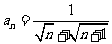 ,求前
,求前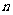 项的和.
项的和.
变式题1、已知数列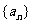 的通项公式为
的通项公式为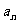 =
=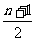 ,设
,设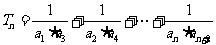 ,求
,求 .
.
解: =
=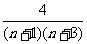 =2(
=2(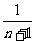 -
- ).
).
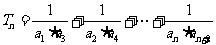 =2[(
=2[(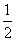 -
-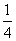 )+(
)+(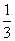 -
-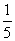 )+(
)+(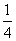 -
-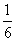 )+……+(
)+……+(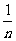 -
-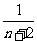 )+(
)+(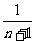 -
- )]=2(
)]=2(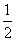 +
+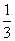 -
-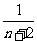 -
- ).
).
变式题2、数列{an}中,a1=8,a4=2,且满足:an+2-2an+1+an=0(n∈N*),
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设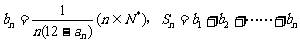 ,是否存在最大的整数m,使得任意的n均有
,是否存在最大的整数m,使得任意的n均有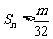 总成立?若存在,求出m;若不存在,请说明理由.
总成立?若存在,求出m;若不存在,请说明理由.
解:(Ⅰ)∵an+2-2an+1+an=0,∴an+2-an+1=an+1-an(n∈N*),
∴{an}是等差数列,设公差为d,
∵a1=8,a4=a1+3d=8+3d=2,∴d=-2,
∴an=8+(n-1)·(-2)=10-2n.
(Ⅱ)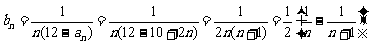
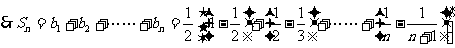
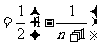
假设存在整数m满足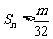 总成立,
总成立,
又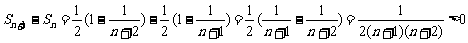
∴数列{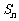 }是单调递增的,
}是单调递增的,
∴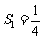 为
为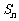 的最小值,故
的最小值,故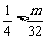 ,即m<8,又m∈N*,
,即m<8,又m∈N*,
∴适当条件的m的最大值为7.
点评:数列求和的裂项相消法:适用于通项公式形如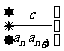 的数列,其中
的数列,其中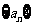 是各项不为0的等差数列,c为常数.
是各项不为0的等差数列,c为常数.
3、(江苏版第62页习题9)利用等比数列的前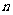 项和公式证明
项和公式证明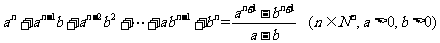
变式题、(2005天津卷18)已知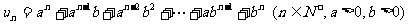 .当
.当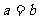 时,求数列
时,求数列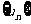 的前n项和
的前n项和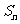 .
.
解:(Ⅰ)当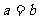 时,
时,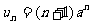 .这时数列
.这时数列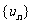 的前
的前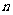 项和
项和
 . ①
. ①
①式两边同乘以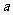 ,得
,得 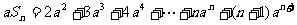 ②
②
①式减去②式,得 
若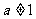 ,
,
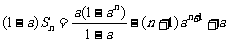 ,
,
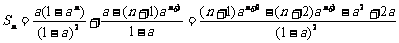
若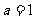 ,
,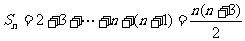
点评:在使用等比数列的求和公式时,要注意对公比q的讨论,即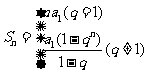 ,这是学生平时容易忽略的问题,应引起足够的重视,另外要求学生有运算化简的能力.
,这是学生平时容易忽略的问题,应引起足够的重视,另外要求学生有运算化简的能力.
2、(江苏版第58页习题6)求和: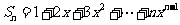
变式题1、已知数列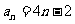 和
和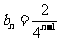 ,设
,设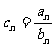 ,求数列
,求数列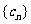 的前
的前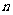 项和
项和 .
.
解: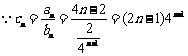 ,
,
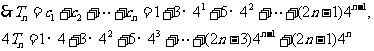
两式相减得
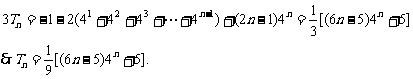
变式题2、(2007全国1文21)设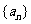 是等差数列,
是等差数列,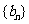 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且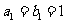 ,
,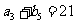 ,
,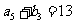 (Ⅰ)求
(Ⅰ)求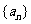 ,
,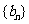 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列 的前n项和
的前n项和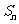 .
.
解:(Ⅰ)设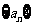 的公差为
的公差为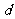 ,
,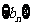 的公比为
的公比为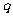 ,则依题意有
,则依题意有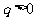 且
且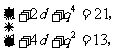
解得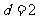 ,
,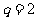 .所以
.所以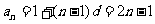 ,
,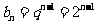 .
.
(Ⅱ)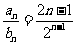 .
.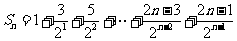 ,①
,①
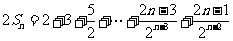 ,②
,②
②-①得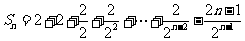 ,
,
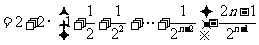
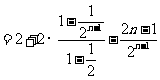
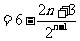 .
.
点评:错位相减法适用于通项公式形容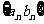 的数列,其中{
的数列,其中{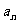 }是等差数列,
}是等差数列,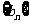 是各项不为0的等比数列.
是各项不为0的等比数列.
变式题2.设等比数列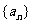 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
.
分析:本题主要考查等比数列的求和公式,等差数列的概念运用,可直接求得.
解: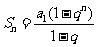 ,
,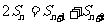 ,则有
,则有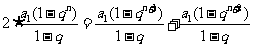 ,
,
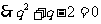 ,
,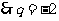 .,若
.,若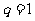 ,则
,则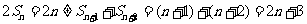 。
。
1、(北师大版第23页习题4)已知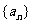 是等差数列,其中
是等差数列,其中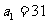 ,公差
,公差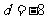 。(1)求数列
。(1)求数列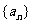 的通项公式,并作出它的图像;(2)数列
的通项公式,并作出它的图像;(2)数列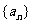 从哪一项开始小于0?(3)求数列
从哪一项开始小于0?(3)求数列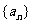 前
前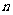 项和的最大值,并求出对应
项和的最大值,并求出对应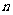 的值.
的值.
变式题1、已知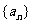 是各项不为零的等差数列,其中
是各项不为零的等差数列,其中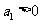 ,公差
,公差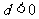 ,若
,若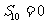 ,求数列
,求数列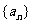 前
前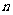 项和的最大值.
项和的最大值.
解: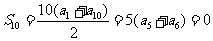 ,所以
,所以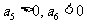 ,即数列
,即数列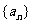 前5项和为最大值.
前5项和为最大值.
变式题2、在等差数列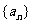 中,
中,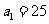 ,
,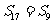 ,求
,求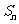 的最大值.
的最大值.
解法一:由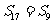 ,得:
,得: ,解得
,解得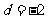 .
.
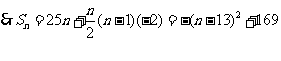 .
.
由二次函数的性质,当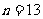 时,
时,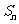 有最大值169.
有最大值169.
解法二:先求出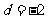 ,
,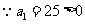 ,
,
由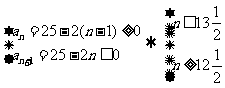 ,所以当
,所以当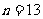 时,
时,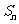 有最大值169.
有最大值169.
解法三:由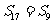 ,得
,得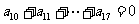 ,而
,而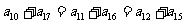
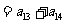 ,故
,故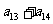 =0.
=0.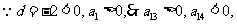 故当
故当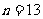 时,
时,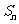 有最大值169.
有最大值169.
点评:解决等差数列前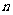 项和最值问题的方法通常有:①、利用二次函数求最值;②、利用通项公式
项和最值问题的方法通常有:①、利用二次函数求最值;②、利用通项公式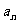 求
求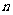 使得
使得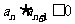 ;③利用性质求出符号改变项.
;③利用性质求出符号改变项.
2、(北师大版第21页习题4)设数列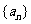 是单调递增的等差数列,前三项的和为12,前三项的积为48,则它的首项是( )
是单调递增的等差数列,前三项的和为12,前三项的积为48,则它的首项是( )
A.1 B.2 C.4 D.8
变式题1、在各项都为正数的等比数列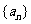 中,首项
中,首项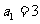 ,前三项和为21,则
,前三项和为21,则 ( )
( )
(A)33 (B)72(C)84(D)189
分析:本题主要是考查等比数列的基本概念和性质,可利用方程思想将等比数列问题转化为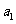 和
和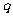 处理,也可利用等比数列的定义进行求解.
处理,也可利用等比数列的定义进行求解.
解法一:设公比为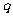 ,由题知,
,由题知,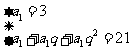 得
得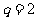 或
或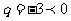 (舍去),∴
(舍去),∴ ,故选C.
,故选C.
解法二:由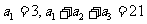 得,
得,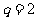 (
(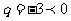 舍去),
舍去),
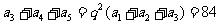 .
.
1、(北师大版第35页习题3)一个等比数列前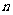 项的和为48,前2
项的和为48,前2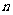 项的和为60,则前3
项的和为60,则前3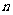 项的和为( )
项的和为( )
A.83 B.108 C.75 D.63
变式题1、一个等差数列前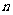 项的和为48,前2
项的和为48,前2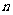 项的和为60,则前3
项的和为60,则前3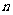 项的和为
。
项的和为
。
解:若数列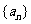 为等差数列,则
为等差数列,则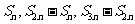 等差数列,可得:48,12,
等差数列,可得:48,12,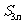 -60成等差数列,所以
-60成等差数列,所以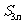 =36.
=36.
变式题2、(江苏版第76页习题1)等比数列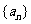 的各项为正数,且
的各项为正数,且 ( )
( )
A.12 B.10 C.8 D.2+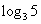
解:因为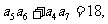 所以
所以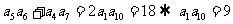 ,而
,而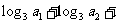
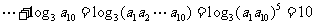 ,所以选B.
,所以选B.
点评:高考试题的一个重要特点就是考查学生对问题敏锐的观察能力和迅速有效的思维能力,灵活运用数学知识和性质可提高我们的正确解题的速度. 因此,对相关知识的性质要深刻地理解和掌握并能灵活运用.
3、待定系数求通项:(人教版第38页习题4)写出下列数列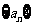 的前5项:(1)
的前5项:(1)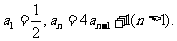
变式题1、(2006年福建卷)已知数列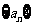 满足
满足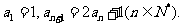 求数列
求数列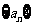 的通项公式;
的通项公式;
解: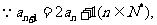
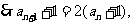
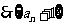 是以
是以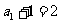 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.

即 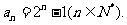
2、解方程求通项:(北师大版第19页习题3)
在等差数列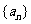 中,(1)已知
中,(1)已知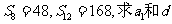 ;(2)已知
;(2)已知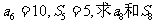 ;(3)已知
;(3)已知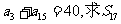 .
.
变式题1、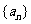 是首项
是首项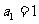 ,公差
,公差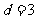 的等差数列,如果
的等差数列,如果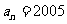 ,则序号
,则序号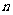 等于
等于
(A)667 (B)668 (C)669 (D)670
分析:本题考查等差数列的通项公式,运用公式直接求出.
解: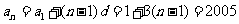 ,解得
,解得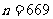 ,选C
,选C
点评:等差等比数列的通项公式和前n项和的公式是数列中的基础知识,必须牢固掌握.而这些公式也可视作方程,利用方程思想解决问题.
1、利用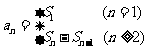 求通项.
求通项.
(北师大版第23页习题5)数列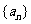 的前
的前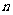 项和
项和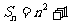 .(1)试写出数列的前5项;(2)数列
.(1)试写出数列的前5项;(2)数列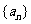 是等差数列吗?(3)你能写出数列
是等差数列吗?(3)你能写出数列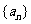 的通项公式吗?
的通项公式吗?
变式题1、(2005湖北卷)设数列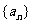 的前n项和为Sn=2n2,求数列
的前n项和为Sn=2n2,求数列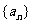 的通项公式;
的通项公式;
解:(1):当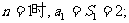
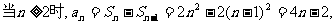
故{an}的通项公式为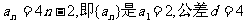 的等差数列.
的等差数列.
变式题2、(2005北京卷)数列{an}的前n项和为Sn,且a1=1,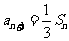 ,n=1,2,3,……,求a2,a3,a4的值及数列{an}的通项公式.
,n=1,2,3,……,求a2,a3,a4的值及数列{an}的通项公式.
解:(I)由a1=1,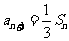 ,n=1,2,3,……,得
,n=1,2,3,……,得
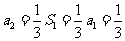 ,
,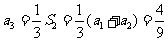 ,
,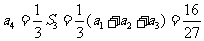 ,
,
由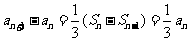 (n≥2),得
(n≥2),得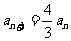 (n≥2),
(n≥2),
又a2=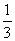 ,所以an=
,所以an=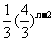 (n≥2),
(n≥2),
∴ 数列{an}的通项公式为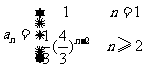
变式题3、(2005山东卷)已知数列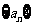 的首项
的首项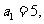 前
前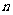 项和为
项和为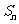 ,且
,且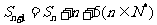 ,
,
证明数列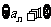 是等比数列.
是等比数列.
解:由已知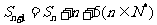 可得
可得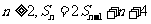 两式相减得
两式相减得
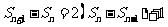 即
即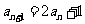 从而
从而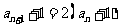 当
当 时
时 所以
所以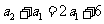 又
又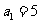 所以
所以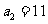 从而
从而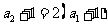
故总有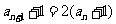 ,
,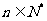 又
又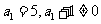 从而
从而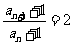 即数列
即数列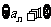 是等比数列;
是等比数列;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com