
8、在某种新型材料的研制中,实验人员获得了下列一组实验数据.现准备用下列四个函数
中的一个近似地表示这些数据的规律,其中最接近的一个是 ( )

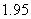
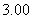
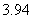
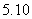

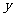
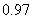
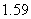
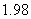
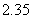
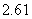
A、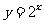 B、
B、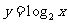 C、
C、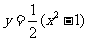 D、
D、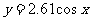
7、函数y=Asin(ωx+φ)在一个周期上的图象如下.则函数的解析式是 ( )
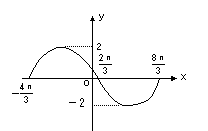 A.y=2sin(+)
A.y=2sin(+)
B.y=2sin(-)
C.y=2sin(+)
D.y=2sin(-)
6、用二分法求函数f(x)=x3+x2-2x-2的一个零点,依次计算得到下列函数值:
|
f(1)=-2 |
f(1.5)=0.625 |
|
f(1.25)=-0.984 |
f(1.375)=-0.260 |
|
f(1.438)=0.165 |
f(1.4065)=-0.052 |
那么方程x3+x2-2x-2=0的一个近似根在下列哪两数之间? ( )
A.1.25-1.375 B.1.375-1.4065
C.1.4065-1.438 D.1.438-1.5
5、函数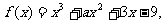 已知
已知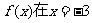 时取得极值,则
时取得极值,则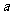 = ( )
= ( )
A.2 B.3 C.4 D.5
4、函数 的定义域是 ( )
的定义域是 ( )
A. B.
B.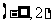 C.
C.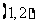 D.
D.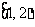
3、设曲线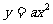 在点(1,
在点(1,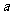 )处的切线与直线
)处的切线与直线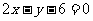 平行,则
平行,则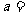 ( )
( )
A.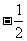 B.
B.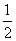 C.1 D.
C.1 D.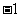
2、三个数a=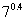 ,b=
,b=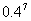 ,c=
,c=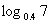 的大小顺序是 ( )
的大小顺序是 ( )
A.a>b>c B.a>c>b C.b>a>c D.c>b>a
1、设A={a,b},集合B={a+1,5},若A∩B={2},则A∪B= ( )
A.{1,2} B.{1,5} C.{2,5} D.{1,2,5}
10、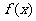 是定义在[-1,1]上的奇函数,且对任意a,b∈[-1,1],a+b≠0,都有
是定义在[-1,1]上的奇函数,且对任意a,b∈[-1,1],a+b≠0,都有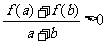 成立,
成立,
(1)若a>b试比较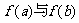 的大小;
的大小;
(2)解不等式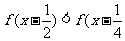 ;
;
(3)若-1≤c≤2,证明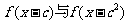 存在公共的定义域。
存在公共的定义域。
解:(1)a>b则a-b>0,又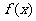 是定义在[-1,1]上的奇函数
是定义在[-1,1]上的奇函数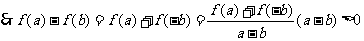
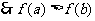
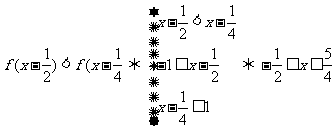
(2)
证明(3)由
此不等式组有解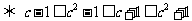 ①
①
或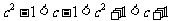 ②
②
由①得: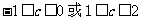 ,此时有公共定义域
,此时有公共定义域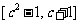
由②得:0<c<1,此时有公共定义域
法二:-1≤c≤2时,作差比较知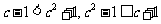 ,必有公共的定义域。……
,必有公共的定义域。……
[探索题](2006上海)已知函数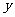 =
=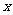 +
+ 有如下性质:如果常数
有如下性质:如果常数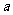 >0,那么该函数在
>0,那么该函数在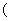 0,
0,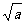
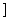 上是减函数,在
上是减函数,在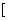
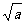 ,+∞
,+∞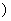 上是增函数
上是增函数
(1)如果函数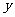 =
=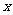 +
+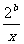 (
(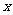 >0)的值域为
>0)的值域为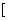 6,+∞
6,+∞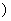 ,求
,求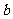 的值;
的值;
(2)研究函数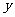 =
=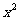 +
+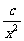 (常数
(常数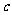 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(3)对函数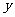 =
=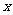 +
+ 和
和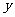 =
=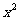 +
+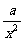 (常数
(常数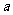 >0)作出推广,使它们都是你所推广的函数的特例
>0)作出推广,使它们都是你所推广的函数的特例 研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
研究推广后的函数的单调性(只须写出结论,不必证明),并求函数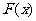 =
=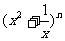 +
+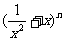 (
(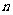 是正整数)在区间[
是正整数)在区间[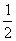 ,2]上的最大值和最小值(可利用你的研究结论)
,2]上的最大值和最小值(可利用你的研究结论)
[解](1)函数y=x+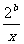 (x>0)的最小值是2
(x>0)的最小值是2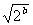 ,则2
,则2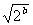 =6, ∴b=log29
=6, ∴b=log29
(2) 设0<x1<x2,y2-y1=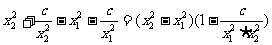
当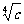 <x1<x2时, y2>y1, 函数y=
<x1<x2时, y2>y1, 函数y=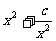 在[
在[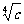 ,+∞)上是增函数;
,+∞)上是增函数;
当0<x1<x2<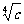 时y2<y1, 函数y=
时y2<y1, 函数y= 在(0,
在(0,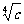 ]上是减函数
]上是减函数
又y= 是偶函数,于是,
是偶函数,于是,
该函数在(-∞,-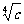 ]上是减函数, 在[-
]上是减函数, 在[-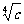 ,0)上是增函数;
,0)上是增函数;
(3) 可以把函数推广为y=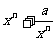 (常数a>0),其中n是正整数
(常数a>0),其中n是正整数
当n是奇数时,函数y= 在(0,
在(0,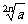 ]上是减函数,在[
]上是减函数,在[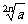 ,+∞) 上是增函数,
,+∞) 上是增函数,
在(-∞,-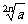 ]上是增函数, 在[-
]上是增函数, 在[-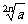 ,0)上是减函数;
,0)上是减函数;
当n是偶数时,函数y= 在(0,
在(0,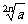 ]上是减函数,在[
]上是减函数,在[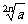 ,+∞) 上是增函数,
,+∞) 上是增函数,
在(-∞,-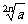 ]上是减函数, 在[-
]上是减函数, 在[-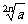 ,0)上是增函数;
,0)上是增函数;
F(x)=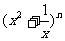 +
+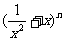 =
=
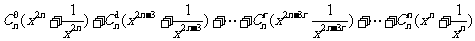 因此F(x) 在 [
因此F(x) 在 [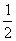 ,1]上是减函数,在[1,2]上是增函数
,1]上是减函数,在[1,2]上是增函数
所以,当x=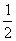 或x=2时,F(x)取得最大值(
或x=2时,F(x)取得最大值(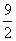 )n+(
)n+(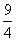 )n;
)n;
当x=1时F(x)取得最小值2n+1
9、函数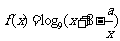 在
在 上是增函数,求
上是增函数,求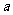 的取值范围
的取值范围
分析:由函数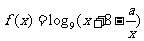 在
在 上是增函数可以得到两个信息:①对任意的
上是增函数可以得到两个信息:①对任意的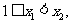 总有
总有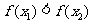 ;②当
;②当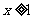 时,
时,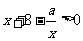 恒成立
恒成立
解:∵函数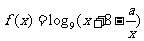 在
在 上是增函数,
上是增函数,
∴对任意的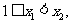 有
有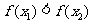 ,
,
即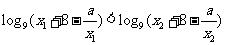 ,得
,得
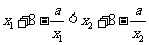 ,即
,即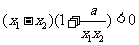 ,
,
∵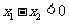 ,∴
,∴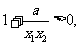
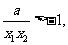
 ,
,
∵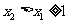 ,∴要使
,∴要使 恒成立,只要
恒成立,只要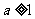 ;
;
又∵函数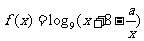 在
在 上是增函数,∴
上是增函数,∴ ,
,
即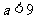 ,综上
,综上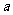 的取值范围为
的取值范围为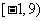

另解:(用导数求解)
令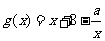 ,函数
,函数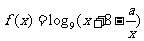 在
在 上是增函数,
上是增函数,
∴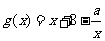 在
在 上是增函数,
上是增函数,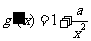 ,
,
∴ ,且
,且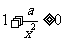 在
在 上恒成立,得
上恒成立,得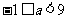
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com