
9、已知函数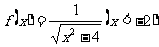 。
。
(1)求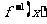 ;
;
(2)设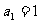 ,
,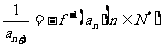 ,求
,求 ;
;
(3)设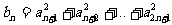 ,是否存在最小正整数m,使对任意
,是否存在最小正整数m,使对任意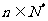 ,有
,有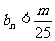 成立?若存在,求出m的值;若不存在,请说明理由。
成立?若存在,求出m的值;若不存在,请说明理由。
8.学校餐厅每天供应1000名学生用餐,每星期一有两种菜谱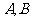 可供选择(每人选一种),调查表明:凡是在星期一选A菜谱的,下星期一会有20%改选B,而选B的,下星期一则有30%改选A,若用
可供选择(每人选一种),调查表明:凡是在星期一选A菜谱的,下星期一会有20%改选B,而选B的,下星期一则有30%改选A,若用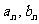 分别表示在第n个星期一选A、B的人数。
分别表示在第n个星期一选A、B的人数。
(1)试用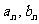 表示
表示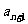 ; (2)证明:
; (2)证明: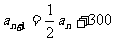 。
。
7.若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号) ①S1与S2; ②a2与S3; ③a1与an; ④q与an. 其中n为大于1的整数, Sn为{an}的前n项和.
6.定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列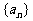 是等和数列,且
是等和数列,且 ,公和为5,那么
,公和为5,那么 的值为______,这个数列的前n项和
的值为______,这个数列的前n项和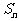 的计算公式为___ .
的计算公式为___ .
5.已知数列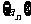 中,
中,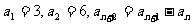 ,则
,则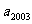 等于
(
)
等于
(
)
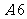
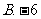
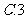
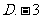
4、在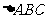 中,
中,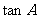 是以-4为第三项,4为第七项的等差数列的公差,
是以-4为第三项,4为第七项的等差数列的公差, 是以
是以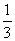 为第三项,9为第六项的等比数列的公比,则该三角形是
(
)
为第三项,9为第六项的等比数列的公比,则该三角形是
(
)
 锐角三角形
锐角三角形  直角三角形
直角三角形
 钝角三角形
钝角三角形  等腰三角形
等腰三角形
3.1999年11月1日起,全国储蓄存款开始征收利息税,利息税的税率为20%,若将1万元人民币存入银行,年利率为2.25%,则1年后到期时,应得本金和利息共计( )
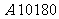 元
元
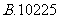 元
元
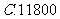 元
元
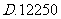 元
元
2.数列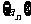 前
前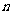 项和
项和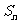 与通项
与通项 满足关系式:
满足关系式: ,则
,则 的值为
(
)
的值为
(
)
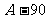
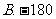
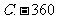


1.已知数列{an},“对任意的nÎN*,点Pn(n,an)都在直线y=3x+2上”是“{an}为等差数列”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3. 数列与平面解几何,注意用坐标与曲线的关系来打开解题思路,平时练习中还是此类问题可联系起来看
冲刺强化训练(13)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com