
25.(本小题满分10分)
在实施“中小学校舍安全工程”之际,某市计划对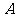 、
、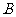 两类学校的校舍进行改造,根据预算,改造一所
两类学校的校舍进行改造,根据预算,改造一所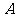 类学校和三所
类学校和三所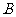 类学校的校舍共需资金480万元,改造三所
类学校的校舍共需资金480万元,改造三所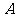 类学校和一所
类学校和一所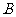 类学校的校舍共需资金400万元.
类学校的校舍共需资金400万元.
(1)改造一所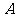 类学校的校舍和一所
类学校的校舍和一所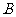 类学校的校舍所需资金分别是多少万元?
类学校的校舍所需资金分别是多少万元?
(2)该市某县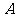 、
、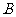 两类学校共有8所需要改造.改造资金由国家财政和地方财政共同承担,若国家财政拨付的改造资金不超过770万元,地方财政投入的资金不少于210万元,其中地方财政投入到
两类学校共有8所需要改造.改造资金由国家财政和地方财政共同承担,若国家财政拨付的改造资金不超过770万元,地方财政投入的资金不少于210万元,其中地方财政投入到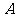 、
、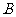 两类学校的改造资金分别为每所20万元和30万元,请你通过计算求出有几种改造方案,每个方案中
两类学校的改造资金分别为每所20万元和30万元,请你通过计算求出有几种改造方案,每个方案中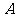 、
、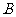 两类学校各有几所.
两类学校各有几所.
24.(本小题满分9分)
如图,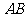 为
为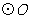 的直径,劣弧
的直径,劣弧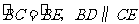 ,连接
,连接 并延长交
并延长交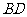 于
于 .
.
求证:(1)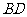 是
是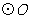 的切线;
的切线;
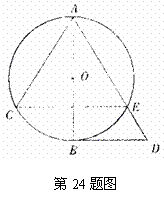 (2)
(2)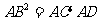 .
.
23.(本小题满分7分)
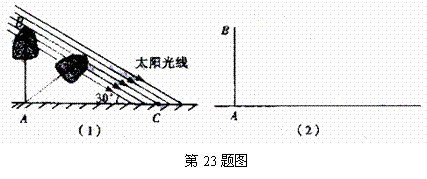
某数学兴趣小组,利用树影测量树高,如图(1),已测出树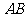 的影长
的影长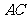 为12米,并测出此时太阳光线与地面成
为12米,并测出此时太阳光线与地面成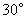 夹角.
夹角.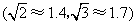
(1)求出树高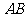 ;
;
(2)因水土流失,此时树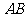 沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.(用图(2)解答)
沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.(用图(2)解答)
①求树与地面成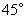 角时的影长;
角时的影长;
②求树的最大影长.
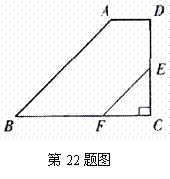
22.(本小题满分8分)
如图,在梯形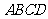 中,
中, 为
为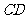 的中点,
的中点,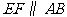 交
交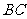 于点
于点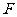 .
.
(1)求证: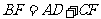 ;
;
(2)当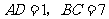 ,且
,且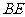 平分
平分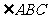 时,求
时,求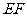 的长.
的长.
21.(本小题满分6分)
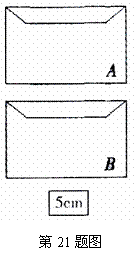 如图,
如图, 信封中装有两张卡片,卡片上分别写着7cm、3cm;
信封中装有两张卡片,卡片上分别写着7cm、3cm; 信封中装有三张卡片,卡片上分别写着2cm、4cm、6cm;信封外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从两个信封中各取出一张卡片,与信封外的卡片放在一起,用卡片上标明的数量分别作三条线段的长度.
信封中装有三张卡片,卡片上分别写着2cm、4cm、6cm;信封外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从两个信封中各取出一张卡片,与信封外的卡片放在一起,用卡片上标明的数量分别作三条线段的长度.
(1)求这三条线段能组成三角形的概率(画出树状图);
(2)求这三条线段能组成直角三角形的概率.
20.(本小题满分7分)
近年来,随着经济的快速发展,我市城市环境不断改观,社会知名度越来越高,吸引了很多外地游客.某旅行社对5月份本社接待外地游客来我市观光的首选景点作了一次抽样调查,调查结果图表如下:
(1)此次共调查了多少人?并将上面的图表补充完整.
(2)如果将上表制成扇形统计图,那么“恩格贝”所对的圆心角是多少度?
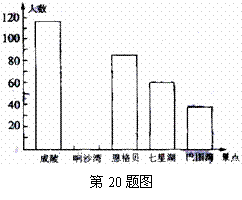 (3)该旅行社预计6月份接待外地来我市的游客2
500人,请你估算一个首选去成陵观光的约有多少人?
(3)该旅行社预计6月份接待外地来我市的游客2
500人,请你估算一个首选去成陵观光的约有多少人?
|
景点 |
频数 |
频率 |
|
成陵 |
116 |
29% |
|
响沙湾 |
|
25% |
|
恩格贝 |
84 |
21% |
|
七星湖 |
63 |
15.75% |
|
巴图湾 |
37 |
9.25% |
19.(本小题满分8分)
(1)计算: ;
;
(2)先化简:再求值: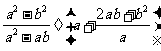 ,其中
,其中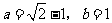 .
.
18.如图,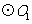 和
和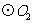 的半径分别为1和2,连接
的半径分别为1和2,连接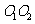 ,交
,交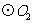 于点
于点 ,
,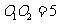 ,若将
,若将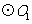 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转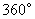 ,则
,则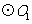 与
与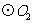 共相切_________次.
共相切_________次.
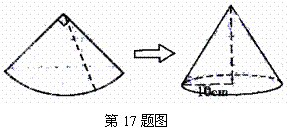
17.如图,现有圆心角为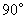 的一个扇形纸片,该扇形的半径为50cm.小红同学为了在“圣诞”节联欢晚会上表演节目,她打算剪去部分扇形纸片后,利用剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),那么被剪去的扇形纸片的圆心角应该是______度.
的一个扇形纸片,该扇形的半径为50cm.小红同学为了在“圣诞”节联欢晚会上表演节目,她打算剪去部分扇形纸片后,利用剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),那么被剪去的扇形纸片的圆心角应该是______度.


16.
 已知关于
已知关于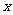 的方程
的方程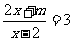 的解是正数,则
的解是正数,则 的取值范围为________.
的取值范围为________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com