
2. 求值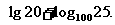
例2.设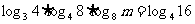 ,求m的值.
,求m的值.
解:∵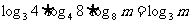 ,
, 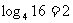
∴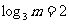 ,即m=9.
,即m=9.
例3.计算:①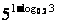 , ②
, ②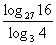 .
.
解:①原式 =  .
.
②∵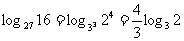 ,
,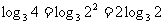 , ∴原式=
, ∴原式=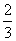 .
.
例4.P67例6
生物机体内碳14的“半衰期”为5730年,湖南长沙马王堆汉墓女尸出土时碳14的残余量约占76.7%,
试推算马王堆古墓的年代.
例5.已知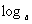 x=
x=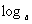 c+b,求x.
c+b,求x.
分析:由于x作为真数,故可直接利用对数定义求解;另外,由于等式右端为两实数和的形式,b的存在使变形产生困难,故可考虑将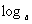 c移到等式左端,或者将b变为对数形式.
c移到等式左端,或者将b变为对数形式.
解法一: 由对数定义可知: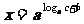
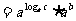
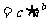 .
.
解法二: 由已知移项可得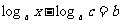 ,即
,即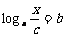 .
.
由对数定义知: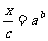
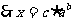 .
.
解法三: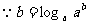
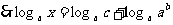
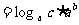
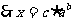 .
.
.
练习:教材P68第4题
例1 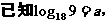
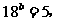
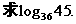
练
1. 已知 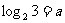 ,
, 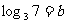 , 用 a, b 表示
, 用 a, b 表示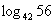 .
.
解:因为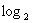 3 = a,则
3 = a,则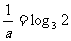 , 又∵
, 又∵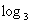 7 = b,
7 = b,
∴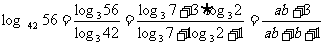 .
.
2.两个常用的推论:
①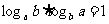 ,
, 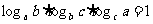 .
.
② 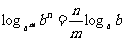 (a,b>0且均不为1).
(a,b>0且均不为1).
证:①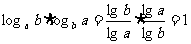 ;
;
②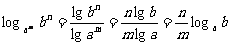 .
.
1.对数换底公式: 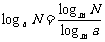 ( a>0 ,a ¹ 1 ,m>0 ,m ¹ 1,N>0).
( a>0 ,a ¹ 1 ,m>0 ,m ¹ 1,N>0).
证明:设
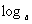 N = x , 则
N = x , 则 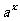 =
N.
=
N.
两边取以m 为底的对数: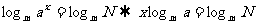
从而得: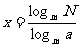 ∴
∴ 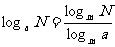 .
.
对数的运算法则
如果 a>0,a ¹ 1,M>0, N>0 有:
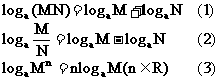
2.作业:《习案》作业二十
⑴对数的定义; ⑵指数式与对数式互换; ⑶求对数式的值.
4.求下列各式的值
(1) 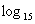 15 ⑵
15 ⑵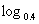 1 ⑶
1 ⑶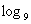 81 ⑷
81 ⑷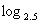 6.25 ⑸
6.25 ⑸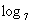 343 ⑹
343 ⑹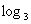 243
243
解:(1) 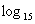 15=1 (2)
15=1 (2) 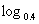 1=0 (3)
1=0 (3) 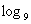 81=2
81=2
(4) 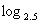 6.25=2 (5)
6.25=2 (5) 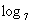 343=3 (6)
343=3 (6) 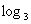 243=5
243=5
3.求下列各式的值
(1) 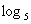 25
⑵
25
⑵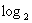
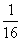 ⑶
⑶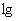 100
100
⑷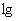 0.01
⑸
0.01
⑸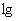 10000
⑹
10000
⑹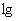 0.0001
0.0001
解:(1) 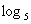 25=
25=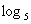
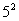 =2 (2)
=2 (2) 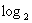
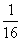 =-4 (3)
=-4 (3) 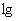 100=2
100=2
(4) 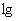 0.01=-2
(5)
0.01=-2
(5) 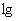 10000=4 (6)
10000=4 (6) 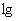 0.0001=-4
0.0001=-4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com