
1.已知a>0,函数f(x)=x3-ax在[1,+∞)上是单调增函数,则a的最大值是
A0 B1 C2 D3
3.求可导函数f(x)的最值的方法:
(1)求f(x)在给定区间内的极值;
(2)将f(x)的各极值与端点值比较,其中最大的一个是最大值,最小的一个是最小值.
(3)如果开区间内只有一个极值点,那么必是最值点。
同步练习 11.4函数的单调性与极值 最值
[选择题]
2.求可导函数f(x)的极值的步骤如下:
(1)求f(x)的定义域,求 (x);
(x);
(2)由 (x)=0,求其稳定点;
(x)=0,求其稳定点;
(3)检查 (x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取极大值;如果左负右正,那么f(x)在这个根处取极小值;如果左右同号,那么f(x)在这个根处不取极值.
(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取极大值;如果左负右正,那么f(x)在这个根处取极小值;如果左右同号,那么f(x)在这个根处不取极值.
注意: f/(x)=0 是函数f(x)在点x0处取极值的必要不充分条件。.
1. 若f(x)在区间(a,b)上可导,则 (x)>0
(x)>0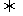 f(x)为增函数(
f(x)为增函数( (x)<0
(x)<0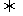 f(x)为减函数).
f(x)为减函数).
(1)若不是可导函数,上述必要性不成立;
(2) (x)≥0(≤0)且只在一些孤立的点处f/(x)=0,则f(x)仍递增(减)。
(x)≥0(≤0)且只在一些孤立的点处f/(x)=0,则f(x)仍递增(减)。
[例1]已知函数f(x)=2ax-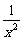 ,x∈(0,1].
,x∈(0,1].
(1)若f(x)在x∈(0,1]上是增函数,求a的取值范围;
(2)求f(x)在区间(0,1]上的最大值.
分析:(1)要使f(x)在(0,1]上为增函数,需f′(x)>0,x∈(0,1).
(2)利用函数的单调性求最大值.
解:(1)由已知可得f′(x)=2a+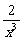 ,∵f(x)在(0,1)上是增函数,∴f′(x)>0,即a>-
,∵f(x)在(0,1)上是增函数,∴f′(x)>0,即a>- , x∈(0,1].∴a>-1.
, x∈(0,1].∴a>-1.
当a=-1时,f′(x)=-2+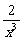 对x∈(0,1)也有f′(x)>0,满足f(x)在(0,1]上为增函数,
对x∈(0,1)也有f′(x)>0,满足f(x)在(0,1]上为增函数,
∴a≥-1.
(2)由(1)知,当a≥-1时,f(x)在(0,1]上为增函数,
∴[f(x)]max=f(1)=2a-1.
当a<-1时,令f′(x)=0得x=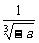 ,
,
∵0<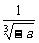 <1,∴0<x<
<1,∴0<x<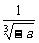 时,f′(x)>0;
时,f′(x)>0;
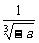 <x≤1时,f′(x)<0.
<x≤1时,f′(x)<0.
∴f(x)在(0,
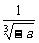 )上是增函数,在(
)上是增函数,在(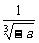 ,1]减函数.
,1]减函数.
∴[f(x)]max=f (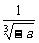 )=-3
)=-3 .
.
解法点评:求参数的取值范围,凡涉及函数的单调性、最值问题时,用导数的知识解决较简单.
[例2] (2006天津) 已知函数 ,其中x∈R,θ为参数,且0≤θ<2π.
,其中x∈R,θ为参数,且0≤θ<2π.
(1)当时cosθ=0,判断函数f(x)是否有极值;
(2)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(3)若对(2)中所求的取值范围内的任意参数θ,函数f(x)在区间 内都是增函数,求实数
内都是增函数,求实数 的取值范围.
的取值范围.
解:(Ⅰ)当cosθ=0时,f(x)=4x3,则f(x)在 内是增函数,故无极值.
内是增函数,故无极值.
(Ⅱ)f′(x)=12x2-6xcosθ,令f′(x)=0,得
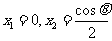
由(Ⅰ),只需分下面两种情况讨论.
①当 cosθ>0时,随x的变化f′(x)的符号及f(x)的变化情况如下表:
cosθ>0时,随x的变化f′(x)的符号及f(x)的变化情况如下表:
|
x |
 |
0 |
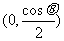 |
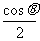 |
 |
|
f/(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
因此,函数f(x)在 处取得极小值
处取得极小值 ,且
,且

要使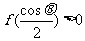 ,必有
,必有 ,可得
,可得
由于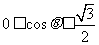 ,故
,故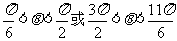
②当时cosθ<0,随x的变化,f′(x)的符号及 的变化情况如下表:
的变化情况如下表:
 |
 |
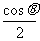 |
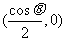 |
 |
 |
 |
+ |
0 |
- |
0 |
+ |
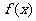 |
 |
极大值 |
 |
极小值 |
 |
因此,函数f(x)在x=0处取得极小值f(0),且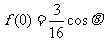
若f(0) >0,则cosx>0。矛盾。所以当cosx<0时,f(x)的极小值不会大于零。
综上,要使函数f(x)在(-∞,+∞)内的极小值大于零,参数θ的取值范围为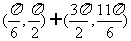 。
。
(III)由(II)知,函数f(x)在区间 与
与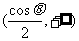 内都是增函数。
内都是增函数。
由题设,函数f(x)在(2a-1,a)内是增函数,则a须满足不等式组
 或
或 
由(II),参数时 时,
时, 。要使不等式
。要使不等式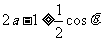 关于参数
关于参数 恒成立,必有
恒成立,必有 ,即
,即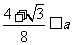 。
。
综上,解得 或
或 。
。
所以 的取值范围是
的取值范围是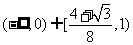 。
。
特别提示:对于求单调区间、极值、最值问题,根据导数的零点把定义区间分开,列出表格,再分析各区间导数的符号,进而确定单调区间、极值最值,清楚直观不易出错。
[例3](2006福建) 统计表明,某种型号的汽车在匀速行驶中每小时的耗油量 (升)关于行驶速度x(千米/小时)的函数解析式可以表示为:
(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: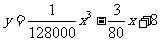 (0<x≤20)已知甲、乙两地相距100千米。
(0<x≤20)已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
解:(I)当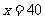 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了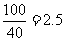 小时,
小时,
要耗油 (升)。
(升)。
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升。
(II)当速度为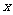 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了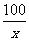 小时,设耗油量为
小时,设耗油量为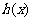 升,
升,
依题意得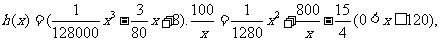

令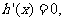 得
得
当 时,
时, 是减函数;
是减函数;
当 时,
时, 是增函数。
是增函数。
 当
当 时,
时,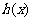 取到极小值
取到极小值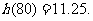
因为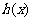 在
在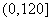 上只有一个极值,所以它是最小值。
上只有一个极值,所以它是最小值。
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升。
考查知识:函数、导数及其应用等基本知识,考查运用数学知识分析和解决实际问题的能力。
[例4](2006广东)
设函数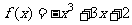 分别在
分别在

 处取得极小值
处取得极小值 极大值
极大值
 平面上点A
平面上点A B的坐标分别为
B的坐标分别为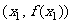

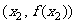 ,该平面上动点P满足
,该平面上动点P满足 ,点Q是点P关于直线
,点Q是点P关于直线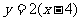 的对称点
的对称点 求(Ⅰ)点A
求(Ⅰ)点A B的坐标
;
B的坐标
;
(Ⅱ)动点Q的轨迹方程
解: (Ⅰ)令 解得
解得
当 时,
时,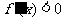 , 当
, 当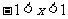 时,
时,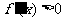 ,当
,当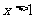 时,
时,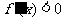
所以,函数在 处取得极小值,在
处取得极小值,在 取得极大值,
取得极大值,
故 ,
,
所以, 点A B的坐标为
B的坐标为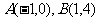

(Ⅱ) 设 ,
,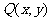 ,PQ的中点在
,PQ的中点在 上,
上,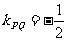 ,
,
所以 ,
,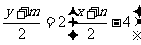
∴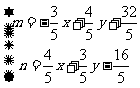
∵
∴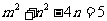
∴
化简得
[研讨.欣赏](2006辽宁)已知函数f(x)=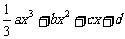 ,其中a , b , c是以d为公差的等差数列,且a>0,d>0.设x0为f(x)的极小值点,在[1-
,其中a , b , c是以d为公差的等差数列,且a>0,d>0.设x0为f(x)的极小值点,在[1-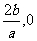 ]上,f/(x)在x1处取得最大值,在x2处取得最小值,将点(x0,f(x0))、(x1,f/(x1))、(x2,f(x2))依次记为A, B, C
]上,f/(x)在x1处取得最大值,在x2处取得最小值,将点(x0,f(x0))、(x1,f/(x1))、(x2,f(x2))依次记为A, B, C
(I)求x0的值
(II)若⊿ABC有一边平行于x轴,且面积为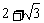 ,求a ,d的值
,求a ,d的值
解(Ⅰ):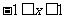

令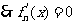 ,得
,得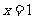 或
或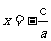

当 时,
时, ,
,
所以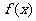 在
在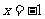 处取极小值,即
处取极小值,即 .
.
(Ⅱ)法一:
∴ 的图象开口向上,对称轴方程是
的图象开口向上,对称轴方程是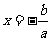 ,
,
 ,知
,知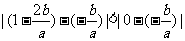
∴ 在
在 上的最大值为
上的最大值为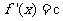 ,则
,则 ,
,
又由 ,知
,知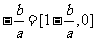
∴当 时,
时, 取得最小值
取得最小值 ,即
,即
 ,
, ,
,
 .
.
由△ABC有一条边平行于x轴,得AC平行于x轴,所以
 ,即
,即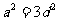 ①
①
又由△ABC的面积为 ,得
,得
 ,
,
利用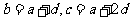 ,得
,得 . ②
. ②
联立①,②可得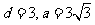 .
.
法二: .
.

由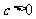 知
知 在
在 上的最大值为
上的最大值为 ,即
,即
由 ,知
,知
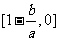 ,
,
∴当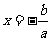 时,
时, 取得最小值
取得最小值 ,即
,即
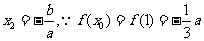 ,
,
 .
.
由△ABC有一条边平行于x轴,得AC平行于x轴,所以
-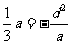 ,即
,即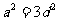 .
①
.
①
又由△ABC的面积为 ,得
,得
 .
.
利用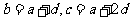 ,得
,得 . ②
. ②
联立①,②可得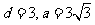 .
.
5.  ; 6.
当x∈(4,5)时,恒有f′(x)>0.答案:③
; 6.
当x∈(4,5)时,恒有f′(x)>0.答案:③
4.y′=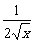 -2, 当0<x<
-2, 当0<x<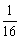 时,y′>0,为增函数.
时,y′>0,为增函数.
当x>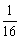 时,y′<0,是减函数.∴x=
时,y′<0,是减函数.∴x=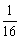 时,y有最大值
时,y有最大值 .
.
6.如果函数y=f(x)的导函数的图象如下图所示,给出下列判断:
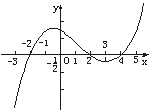
①函数y=f(x)在区间(-3,-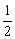 )内单调递增;
)内单调递增;
②函数y=f(x)在区间(-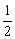 ,3)内单调递减;
,3)内单调递减;
③函数y=f(x)在区间(4,5)内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x=-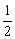 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
则上述判断中正确的是_____________
简答:1-4.DDD;
5.(2006北京)已知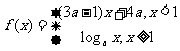 是
是 上的减函数,那么
上的减函数,那么 的取值范围是
的取值范围是
4. 函数y= -2x(x≥0)的最大值为_____________.
-2x(x≥0)的最大值为_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com