
58、(河北省正定中学2008年高三第五次月考)已知 是数列
是数列 的前
的前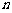 项和,
项和,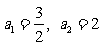 ,且
,且 ,其中
,其中 .
.
(1)求数列 的通项公式
的通项公式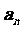 ;
;
(2)(理科)计算 的值. ( 文科) 求
的值. ( 文科) 求  .
.
解:①




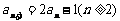 ---------2分
---------2分
又 也满足上式,
也满足上式,


 (
( )
)
 数列
数列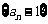 是公比为2,首项为
是公比为2,首项为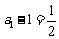 的等比数列
----------- 4分
的等比数列
----------- 4分
 -------------- 6分
-------------- 6分
②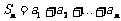

②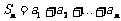


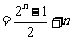 -------------(9分)
-------------(9分)
于是 ---------------(12分)
---------------(12分)
57、已知数列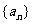 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点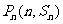 都在函数
都在函数 的图像上,且过点
的图像上,且过点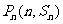 的切线的斜率为
的切线的斜率为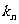 .
.
(1)求数列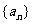 的通项公式.
的通项公式.
(2)若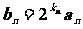 ,求数列
,求数列 的前
的前 项和
项和 .
.
(3)设 ,等差数列
,等差数列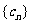 的任一项
的任一项 ,其中
,其中 是
是 中的最小数,
中的最小数,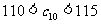 ,求
,求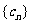 的通项公式.
的通项公式.
解:(1) 点
点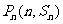 都在函数
都在函数 的图像上,
的图像上,
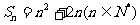 ,
,
当 时,
时,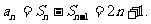
当n=1时,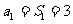 满足上式,所以数列
满足上式,所以数列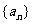 的通项公式为
的通项公式为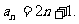 …….3分
…….3分
(2)由 求导可得
求导可得
 过点
过点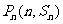 的切线的斜率为
的切线的斜率为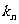 ,
,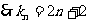 .
.
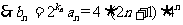 .
.
 ①
①
由①×4,得
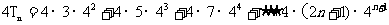 ②
②
①-②得:

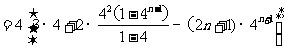
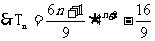 ………………………………………………………………..7分
………………………………………………………………..7分
(3) ,
,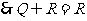 .
.
又 ,其中
,其中 是
是 中的最小数,
中的最小数, .
.
 是公差是4的倍数,
是公差是4的倍数,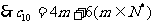 .
.
又 ,
,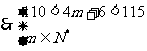 ,解得m=27.
,解得m=27.
所以 ,
,
设等差数列的公差为 ,则
,则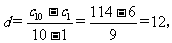
 ,所以
,所以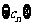 的通项公式为
的通项公式为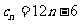 …………12分
…………12分
56、(河北省正定中学高2008届一模)设数列{an}的各项都是正数,且对任意n∈N+,都有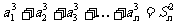 ,记Sn为数列{an}的前n项和.
,记Sn为数列{an}的前n项和.
(1)求数列{an}的通项公式;
(2)若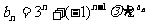 (
(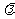 为非零常数,n∈N+),问是否存在整数
为非零常数,n∈N+),问是否存在整数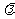 ,使得对任意 n∈N+,都有bn+1>bn.
,使得对任意 n∈N+,都有bn+1>bn.
解:(1)在已知式中,当n=1时,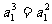
∵a1>0 ∴a1=1………………………………………………………………1分
当n≥2时,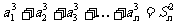 ①
①
 ②
②
①-②得,
∵an>0 ∴ =
=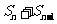 =2Sn-an
=2Sn-an
∵a1=1适合上式…………………………3分.
当n≥2时, 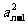 =2Sn-1-an-1 ④
=2Sn-1-an-1 ④
③-④得 -
-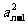 =2(Sn-Sn-1)-an+an-1=2an-an+ an-1= an+ an-1
=2(Sn-Sn-1)-an+an-1=2an-an+ an-1= an+ an-1
∵an+an-1>0 ∴an-an-1=1
∴数列{an}是等差数列,首项为1,公差为1,可得an=n………………5分
(2)∵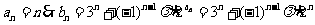
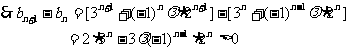
∴ ⑤………………………………………………………….7分
⑤………………………………………………………….7分
当n=2k-1,k=1,2,3,……时,⑤式即为 ⑥
⑥
依题意,⑥式对k=1,2,3……都成立,∴λ<1………………………………..9分
当n=2k,k=1,2,3,…时,⑤式即为 ⑦
⑦
依题意,⑦式对k=1,2,3,……都成立,
∴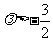 ……………………………………………………………………………..11分
……………………………………………………………………………..11分
∴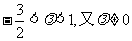
∴存在整数λ=-1,使得对任意n∈N,都有bn+1>bn……………………………12分
55、(河北衡水中学2008年第四次调考)已知等差数列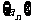 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列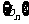 的前n项的和为
的前n项的和为 ,且
,且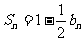 .
.
(1) 求数列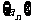 ,
,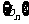 的通项公式;
的通项公式;
(2) 记 ,求证:
,求证: .
.
解:(Ⅰ)∵a3,a5是方程 的两根,且数列
的两根,且数列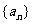 的公差d>0,
的公差d>0,
∴a3=5,a5=9,公差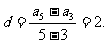
∴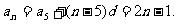 ………………3分
………………3分
又当n=1时,有b1=S1=1-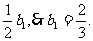
当
∴数列{bn}是等比数列,
∴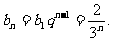 …………6分
…………6分
(Ⅱ)由(Ⅰ)知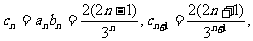 …………9分
…………9分
∴
∴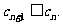 …………………………12分
…………………………12分
54、(安徽省合肥市2008年高三年级第一次质检)已知数列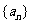 中,
中,
(1)求证:数列 与
与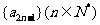 都是等比数列;(2)求数列
都是等比数列;(2)求数列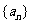 前
前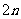 的和
的和 ;
;
(3)若数列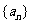 前
前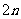 的和为
的和为 ,不等式
,不等式 对
对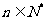 恒成立,求
恒成立,求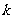 的最大值。
的最大值。
解:(1)∵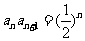 ,∴
,∴ 2分
2分
∴数列 是以1为首项,
是以1为首项, 为公比的等比数列;
为公比的等比数列;
数列 是以
是以 为首项,
为首项, 为公比的等比数列。 4分
为公比的等比数列。 4分
(2)
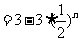 9分
9分
(3)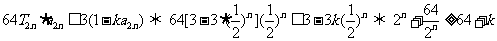
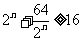 当且仅当
当且仅当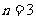 时取等号,所以
时取等号,所以 ,即
,即 ,∴
,∴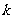 的最大值为-48
的最大值为-48
53、(贵州省贵阳六中、遵义四中2008年高三联考)数列 中,
中, ,
,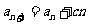 (
(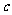 是常数,
是常数, ),且
),且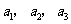 成公比不为
成公比不为 的等比数列。
的等比数列。
(I)求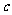 的值;
的值;
(II)求 的通项公式。
的通项公式。
(III)(理做文不做)由数列 中的第1、3、9、27、……项构成一个新的数列{b
中的第1、3、9、27、……项构成一个新的数列{b },求
},求 的值。
的值。
解:(I) ,
, ,
, ,因为
,因为 ,
,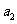 ,
, 成等比数列,
成等比数列,
所以 ,解得
,解得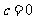 或
或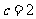 .
.
当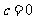 时,
时, ,不符合题意舍去,故
,不符合题意舍去,故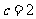 .……理4分(文6分)
.……理4分(文6分)
(II)当 时,由于
时,由于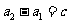 ,
,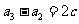 ,……
,……
 ,所以
,所以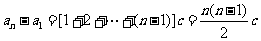 。
。
又 ,
,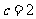 ,故
,故 .当n=1时,上式也成立,所以
.当n=1时,上式也成立,所以 ……理8分(文12分)
……理8分(文12分)
(III)bn=32n-2-3n-1+2,
∴ =9. ……理12分
=9. ……理12分
52、(广东省五校2008年高三上期末联考)已知数列 的前n项和
的前n项和 满足:
满足: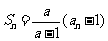 (a为常数,且
(a为常数,且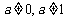 ). (Ⅰ)求
). (Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 ,若数列
,若数列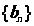 为等比数列,求a的值;
为等比数列,求a的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设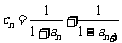 ,数列
,数列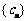 的前n项和为Tn
的前n项和为Tn
求证: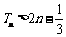 .
.
解:(Ⅰ) ∴
∴
当 时,
时,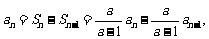
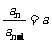 ,即
,即 是等比数列.
∴
是等比数列.
∴ ;
……………………4分
;
……………………4分
(Ⅱ)由(Ⅰ)知, ,若
,若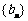 为等比数列,
为等比数列,
则有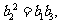 而
而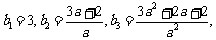
故 ,解得
,解得 , ………………………………7分
, ………………………………7分
再将 代入得
代入得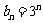 成立,
成立,
所以 .
………………………………………………………………8分
.
………………………………………………………………8分
(III)证明:由(Ⅱ)知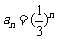 ,所以
,所以

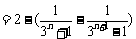 , ………………………………………………… 9分
, ………………………………………………… 9分
由 得
得
所以 ,
…………………… 12分
,
…………………… 12分
从而
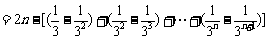
 .
.
即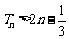 .
…………………………14分
.
…………………………14分
51、(广东省四校联合体第一次联考)已知函数 且任意的
且任意的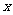 、
、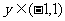 都有
都有
(1)若数列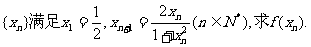
(2)求 的值.
的值.
解:(1)


而
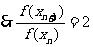
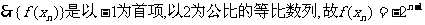
(2)由题设,有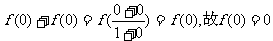
又
得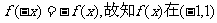 上为奇函数. 由
上为奇函数. 由
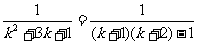

得
于是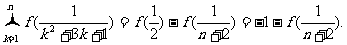
故
47、(上海市部分重点中学2008届高三第二次联考)在等差数列 中,
中,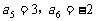 ,则
,则 __________
__________
答案:3
46、(山东省实验中学2008届高三第三次诊断性测试)给出下列命题:
①若 成等比数列;
成等比数列;
②已知函数 的某两个交点的横坐标为
的某两个交点的横坐标为 ;
;
③函数 至多有一个交点;
至多有一个交点;
④函数
其中正确命题的序号是 .
答案:③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com