
6、(安徽省蚌埠二中2008届高三8月月考)已知 是关于x的三次函数,且
是关于x的三次函数,且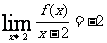 ,
,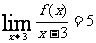 ,则
,则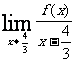 的值是
的值是
(A) 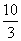 (B)
(B) 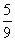 (C) 3 (D) 不存在
答案:A
(C) 3 (D) 不存在
答案:A
5、(安徽省蚌埠二中2008届高三8月月考)函数 在
在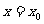 处连续是
处连续是 在
在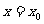 处有极限的
处有极限的
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件 答案:A
4、(江西省五校2008届高三开学联考)已知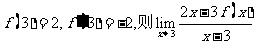
A.-4 B.8 C.0 D.不存在
答案:B
3、(江西省五校2008届高三开学联考)设函数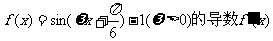 的最大值为3,则f(x)的图象的一条对称轴的方程是
的最大值为3,则f(x)的图象的一条对称轴的方程是
A.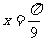 B.
B.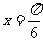
C.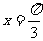 D.
D.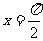
答案:A
2、(安徽省皖南八校2008届高三第一次联考)若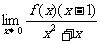 存在,则
存在,则 不可能为( )
不可能为( )
A.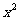 ; B.
; B.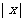 ; C.
; C.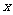 ; D.
; D. ;
;
答案:B
1、(江苏省启东中学2008年高三综合测试一)函数y=2x3-3x2-12x+5在区间[0,3]上最大值与最小值分别是( )
A. 5,-15 B. 5,-4 C. -4,-15 D. 5,-16
答案:A
81、(山西大学附中2008届二月月考)设函数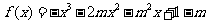 (其中
(其中 )的图象在
)的图象在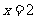 处的切线与直线
处的切线与直线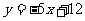 平行.
平行.
(1)求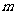 的值;
的值;
(2)求函数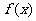 在区间[0,1]的最小值;
在区间[0,1]的最小值;
(3)若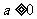 ,
,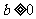 ,
,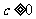 ,且
,且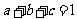 ,
,
试根据上述(Ⅰ)、(Ⅱ)的结论证明: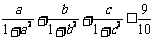 .
.
解:(1)因为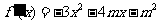 , 所以
, 所以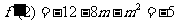
解得m=-1或m=-7(舍),即m=-1 (2)由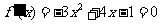 ,解得
,解得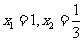
列表如下:
|
x |
0 |
(0,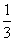 ) ) |
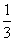 |
(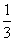 ,1) ,1) |
1 |
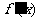 |
|
- |
|
+ |
|
|
f(x) |
2 |
↘ |
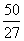 |
↗ |
2 |
所以函数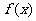 在区间[0,1]的最小值为
在区间[0,1]的最小值为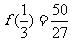
(3)因为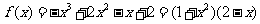
由(2)知,当x∈[0,1]时, 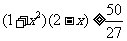 ,所以
,所以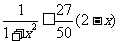 ,
,
所以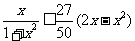
当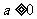 ,
,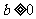 ,
,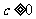 ,且
,且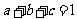 时,
时, 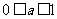 ,
,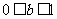 ,
,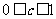 ,所以
,所以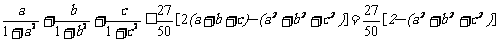
又因为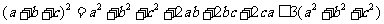 ,
,
所以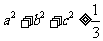
故 (当且仅当
(当且仅当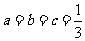 时取等号)
时取等号)
80、(山东省郓城一中2007-2008学年第一学期期末考试)已知函数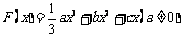 且
且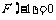
(1)若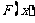 在
在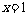 取得极小值-2,求函数
取得极小值-2,求函数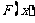 的单调区间
的单调区间
(2)令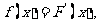 若
若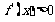 的解集为A,且
的解集为A,且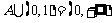 ,求
,求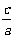 的范围
的范围
解:(I)∵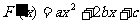 ,且
,且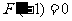 ,
,
∴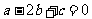 ①④
①④
又由在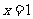 处取得极小值-2可知
处取得极小值-2可知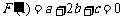 ②且
②且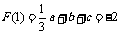 ③
③
将①②③式联立得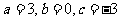 ∴
∴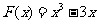 。
。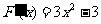 (4分)
(4分)
由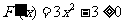 得
得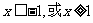 同理由
同理由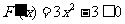 得
得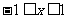
∴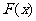 的单调递减区间是[-1,1], 单调递增区间是(-∞,1
的单调递减区间是[-1,1], 单调递增区间是(-∞,1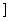 和
和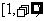 (6分)
(6分)
(II)由上问知: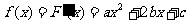 ,∴
,∴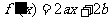 。
。
又∵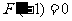 。∴
。∴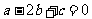 。∴
。∴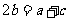 。∴
。∴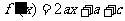
∵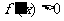 ,∴
,∴ >0。∴
>0。∴ 。(8分)
。(8分)
∴当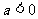 时,
时,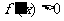 的解集是
的解集是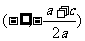 ,
,
显然A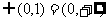 不成立,不满足题意。
不成立,不满足题意。
∴ ,且
,且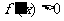 的解集是
的解集是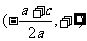 。 (10分)
。 (10分)
又由A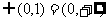 知
知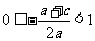 。解得
。解得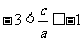 。(12分)
。(12分)
79、(山西省实验中学2007-2008学年度高三年级第四次月考)设函数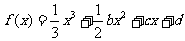 (b、c、d为常数),方程
(b、c、d为常数),方程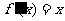 有两个实数x1、x2,且
有两个实数x1、x2,且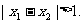
(1)求证: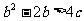
(2)若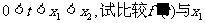 的大小
的大小
(3)若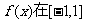 上的切线倾斜角取值范围是
上的切线倾斜角取值范围是
解:(1)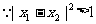

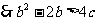 …………4分
…………4分
(2)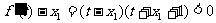
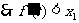 …………8分
…………8分
(3)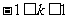

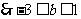 …………12分
…………12分
78、(山东省实验中学2008届高三第三次诊断性测试)已知函数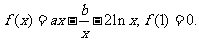
(1)若函数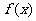 在其定义域内为单调函数,求实数
在其定义域内为单调函数,求实数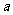 的取值范围;
的取值范围;
(2)若函数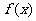 的图象在
的图象在 处的切线的斜率为0,且
处的切线的斜率为0,且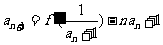 ,若
,若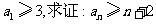 .
.
解:(1)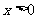
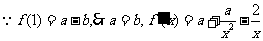
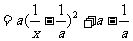 ,(2分)
,(2分)
①当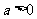 时,则有
时,则有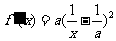
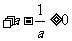 恒成立。即
恒成立。即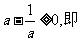
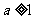
②当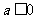 时,由x>0,知
时,由x>0,知 恒成立;
恒成立;
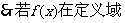 内为单调函数,
内为单调函数,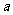 的取值范围为
的取值范围为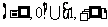 ..….….5分
..….….5分
(2) 函数
函数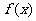 的图象在
的图象在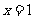 处的切线为斜率为0,
处的切线为斜率为0,
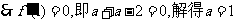 ,
,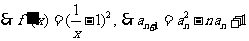 ………8分
………8分
用数学归纳法证明:(Ⅰ)当 时,
时,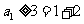 ,不等式成立;
,不等式成立;
(Ⅱ)假设当时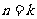 时,不等式成立,即
时,不等式成立,即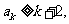 那么,
那么,
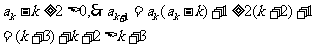
也就是说,当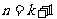 时,
时,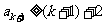 ,根据(Ⅰ)(Ⅱ)对于所有
,根据(Ⅰ)(Ⅱ)对于所有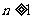 有
有
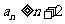 ………………………….12分
………………………….12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com