
57、(湖北省八校高2008第二次联考)已知 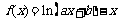 ,其中
,其中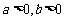 .
.
(Ⅰ)求使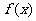 在
在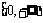 上是减函数的充要条件;
上是减函数的充要条件;
(Ⅱ)求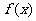 在
在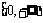 上的最大值;
上的最大值;
(Ⅲ)解不等式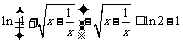 .
.
解:(1) .
. 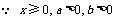 ,
, 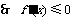 时,
时, ,即
,即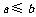 .
.
当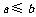 时,
时,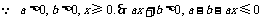 , 即
, 即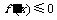 .
.
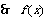 在
在 上是减函数的充要条件为
上是减函数的充要条件为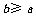 .
………(4分)
.
………(4分)
(2)由(1)知,当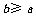 时
时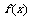 为减函数,
为减函数,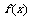 的最大值为
的最大值为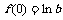 ;
;
当 时,
时, ,
, 当
当 时,
时, ,当
,当 时
时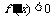 ,
,
即在 上
上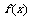 是增函数,在
是增函数,在 上
上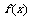 是减函数,
是减函数,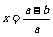 时
时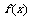 取最大值,
取最大值,
最大值为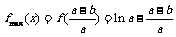 , 即
, 即 ……(13分)
……(13分)
(3)在(1)中取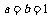 ,即
,即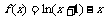 , 由(1)知
, 由(1)知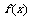 在
在 上是减函数.
上是减函数.
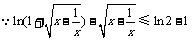 ,即
,即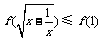 ,
,
 ,解得
,解得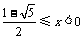 或
或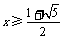 .
.
故所求不等式的解集为[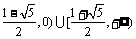 ……………(8分)
……………(8分)
56、(黑龙江省哈师大附中2008届高三上期末)已知a为实数,
(1)若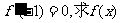 在[-4,4]上的最大值和最小值;
在[-4,4]上的最大值和最小值;
(2)若 上都是递增的,求a的取值范围。
上都是递增的,求a的取值范围。
解:(1)
|
x |
(-∞,-1) |
-1 |
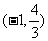 |
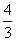 |
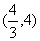 |
 |
+ |
0 |
- |
0 |
+ |
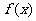 |
增 |
极大 |
减 |
极小 |
增 |
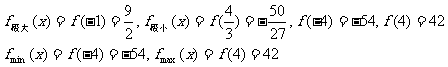
(2) 均成立,
均成立,

55、(黑龙江省哈尔滨三中2008年高三上期末)设函数
(1)如果a=1,求曲线 的切线方程;
的切线方程;
(2)当 恒成立,求a的取值范围。
恒成立,求a的取值范围。
答案:(1)
(2)a≥6
54、(黑龙江省哈尔滨三中2008年高三上期末)已知函数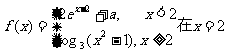 处连续。
处连续。
(1)求实数a的值;
(2)解关于x的不等式
答案:(1)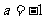
(2)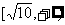
53、(黑龙江省哈尔滨九中2008年第三次模拟考试)已知函数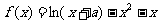 在
在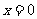 处取得极值,
处取得极值,
(1)求实数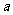 的值;
的值;
(2)若关于 的方程
的方程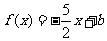 在区间
在区间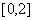 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围.
的取值范围.
解:①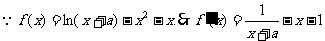
又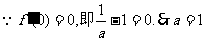 …………4分
…………4分
由
设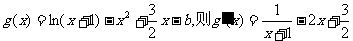
即

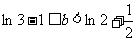 …………12分
…………12分
52、(河南省许昌市2008年上期末质量评估)已知函数f (x)= x2+2ax,g(x)=3a2lnx+b,其中a>0.设两曲线y=f (x),y=g(x)有公共点,且在公共点处的切线相同.
x2+2ax,g(x)=3a2lnx+b,其中a>0.设两曲线y=f (x),y=g(x)有公共点,且在公共点处的切线相同.
(Ⅰ)用a表示b;
(Ⅱ)求证:f (x)≥g(x),(x>0).

51、已知函数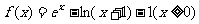 ,
,
(1)求函数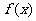 的最小值;
的最小值;
(2)若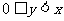 ,求证:
,求证: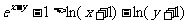 .
.
解:(1) =
=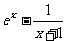 ,………………2分
,………………2分
当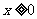 时,
时,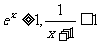 ,所以当
,所以当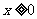 时,
时,
 ,
,
则函数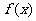 在
在 上单调递增,
上单调递增,
所以函数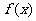 的最小值
的最小值 ;…………………………5分
;…………………………5分
(2)由(1)知,当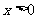 时,
时, ,
,
∵ ,
,
∴ ,
,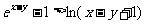 ①……7分
①……7分
∵ ,
,
∴ ②………………………10分
②………………………10分
由①②得
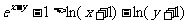 …………………………12分
…………………………12分
25、(江苏省南京市2008届高三第一次调研测试)函数f (x) = x – lnx的单调递减区间是 ▲ .
答案:(0,1]
24、(黄家中学高08级十二月月考)已知数列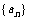 的前n项和是
的前n项和是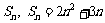 ,则
,则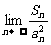 =
=
[解]:∵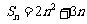 ∴
∴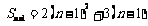
∴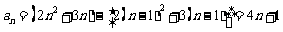 ∴
∴
23、(河南省上蔡一中2008届高三月考)
答案:3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com