7、集合概念及其基本理论是近代数学最基本的内容之一。学会用集合的思想处理数学问题。

6、反证法是中学数学的重要方法。会用反证法证明一些代数命题。

5、充分条件与必要条件

　 (1)定义：对命题“若p则q”而言，当它是真命题时，p是q的充分条件，q是p的必要条件，当它的逆命题为真时，q是p的充分条件，p是q的必要条件，两种命题均为真时，称p是q的充要条件；

　 (2)在判断充分条件及必要条件时，首先要分清哪个命题是条件，哪个命题是结论，其次，结论要分四种情况说明：充分不必要条件，必要不充分条件，充分且必要条件，既不充分又不必要条件。从集合角度看，若记满足条件p的所有对象组成集合A，满足条件q的所有对象组成集合q，则当A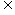B时，p是q的充分条件。B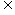A时，p是q的充分条件。A=B时，p是q的充要条件；

(3)当p和q互为充要时，体现了命题等价转换的思想。

4、命题：

(1)命题分类：真命题与假命题，简单命题与复合命题；

(2)复合命题的形式：p且q，p或q，非p；

　 (3)复合命题的真假：对p且q而言，当q、p为真时，其为真；当p、q中有一个为假时，其为假。对p或q而言，当p、q均为假时，其为假；当p、q中有一个为真时，其为真；当p为真时，非p为假；当p为假时，非p为真。

　 (3)四种命题：记“若q则p”为原命题，则否命题为“若非p则非q”，逆命题为“若q则p“，逆否命题为”若非q则非p“。其中互为逆否的两个命题同真假，即等价。因此，四种命题为真的个数只能是偶数个。

3、集合运算

　 (1)交，并，补，定义：A∩B={x|x∈A且x∈B}，A∪B={x|x∈A，或x∈B}，C_UA={x|x∈U，且x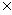A}，集合U表

示全集；

(2)运算律，如A∩(B∪C)=(A∩B)∪(A∩C)，C_U(A∩B)=(C_UA)∪(C_UB)，

C_U(A∪B)=(C_UA)∩(C_UB)等。

2、两类关系：

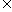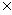(1)元素与集合的关系，用或表示；

　 (2)集合与集合的关系，用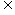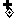，，=表示，当A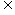B时，称A是B的子集；当A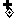B时，称A是B的真子集。

1、集合的概念：

(1)集合中元素特征，确定性，互异性，无序性；

(2)集合的分类：

①按元素个数分：有限集，无限集；

　 　②按元素特征分；数集，点集。如数集{y|y=x²}，表示非负实数集，点集{(x，y)|y=x²}表示开口向上，以y轴为对称轴的抛物线；

(3)集合的表示法：

　　 ①列举法：用来表示有限集或具有显著规律的无限集，如N₊={0，1，2，3，…}；②描述法。

5、学会用定义解题，理解数形结合，分类讨论及等价变换等思想方法。

4、理解充分条件，必要条件及充要条件的意义，会判断两个命题的充要关系；

3、理解逻辑联结词的含义，会熟练地转化四种命题，掌握反证法；