
2、掌握含绝对值不等式及一元二次不等式的解法;
1、理解集合及表示法,掌握子集,全集与补集,子集与并集的定义;
《集合与简易逻辑》复习
4.(2010年江苏23)(本小题满分10分)
已知△ABC的三边长都是有理数。
(1)求证cosA是有理数;
(2)求证:对任意正整数n,cosnA是有理数。
[解析] 本题主要考查余弦定理、数学归纳法等基础知识,考查推理论证的能力与分析问题、解决问题的能力。满分10分。
(方法一)(1)证明:设三边长分别为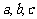 ,
, ,∵
,∵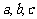 是有理数,
是有理数,
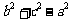 是有理数,分母
是有理数,分母 为正有理数,又有理数集对于除法的具有封闭性,
为正有理数,又有理数集对于除法的具有封闭性,
∴ 必为有理数,∴cosA是有理数。
必为有理数,∴cosA是有理数。
(2)①当 时,显然cosA是有理数;
时,显然cosA是有理数;
当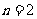 时,∵
时,∵ ,因为cosA是有理数, ∴
,因为cosA是有理数, ∴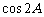 也是有理数;
也是有理数;
②假设当 时,结论成立,即coskA、
时,结论成立,即coskA、 均是有理数。
均是有理数。
当 时,
时, ,
,
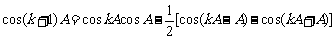 ,
,
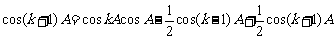 ,
,
解得:
∵cosA, ,
, 均是有理数,∴
均是有理数,∴ 是有理数,
是有理数,
∴ 是有理数。即当
是有理数。即当 时,结论成立。
时,结论成立。
综上所述,对于任意正整数n,cosnA是有理数。
(方法二)证明:(1)由AB、BC、AC为有理数及余弦定理知
 是有理数。
是有理数。
(2)用数学归纳法证明cosnA和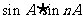 都是有理数。
都是有理数。
①当 时,由(1)知
时,由(1)知 是有理数,从而有
是有理数,从而有 也是有理数。
也是有理数。
②假设当 时,
时,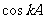 和
和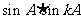 都是有理数。
都是有理数。
当 时,由
时,由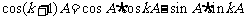 ,
,
 ,
,
及①和归纳假设,知 和
和 都是有理数。
都是有理数。
即当 时,结论成立。综合①、②可知,对任意正整数n,cosnA是有理数。
时,结论成立。综合①、②可知,对任意正整数n,cosnA是有理数。
3.(2010年上海理22)(本题满分18分)
本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分10分。
若实数 、
、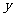 、
、 满足
满足 ,则称
,则称 比
比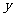 远离
远离 .
.
(1)若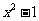 比1远离0,求
比1远离0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、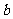 ,证明:
,证明: 比
比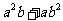 远离
远离 ;
;
(3)已知函数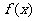 的定义域
的定义域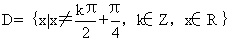 .任取
.任取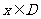 ,
,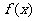 等于
等于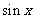 和
和 中远离0的那个值.写出函数
中远离0的那个值.写出函数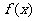 的解析式,并指出它的基本性质(结论不要求证明).
的解析式,并指出它的基本性质(结论不要求证明).
解析:(1)  ;
(2) 对任意两个不相等的正数a、b,有
;
(2) 对任意两个不相等的正数a、b,有 ,
,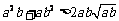 ,
因为
,
因为 ,
所以
,
所以 ,即a3+b3比a2b+ab2远离
,即a3+b3比a2b+ab2远离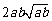 ;
(3)
;
(3)  ,
性质:1°f(x)是偶函数,图像关于y轴对称,2°f(x)是周期函数,最小正周期
,
性质:1°f(x)是偶函数,图像关于y轴对称,2°f(x)是周期函数,最小正周期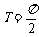 ,
3°函数f(x)在区间
,
3°函数f(x)在区间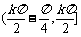 单调递增,在区间
单调递增,在区间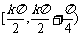 单调递减,kÎZ,
4°函数f(x)的值域为
单调递减,kÎZ,
4°函数f(x)的值域为 .
.
2.(2010年广东理21)(本小题满分14分)
设A(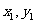 ),B(
),B( )是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离p(A,B)为
)是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离p(A,B)为 .
.

当且仅当 时等号成立,即
时等号成立,即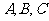 三点共线时等号成立.
三点共线时等号成立.
(2)当点C(x, y) 同时满足①P +P
+P = P
= P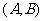 ,②P
,②P = P
= P 时,点
时,点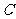 是线段
是线段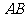 的中点.
的中点. 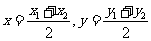 ,即存在点
,即存在点 满足条件。
满足条件。
1.(2010年北京理20)(本小题共13分)
已知集合 对于
对于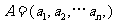 ,
,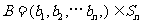 ,定义A与B的差为
,定义A与B的差为
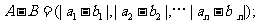
A与B之间的距离为
(Ⅰ)证明: ,且
,且 ;
;
(Ⅱ)证明: 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为 .
.
证明: ≤
≤ .
.
[分析]:这道题目的难点主要出现在读题上,这里简要分析一下。
题目所给的条件其实包含两个定义,第一个是关于 的,其实
的,其实 中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,
也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1,
第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,
也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1,
第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
第一问,因为每个数位上都是0或者1,取差的绝对值仍然是0或者1,符合 的要求。然后是减去C的数位,不管减去的是0还是1,
每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
的要求。然后是减去C的数位,不管减去的是0还是1,
每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
第二问,先比较A和B有几个不同(因为距离就是不同的有几个),然后比较A和C有几个不同,这两者重复的(就是某一位上A和B不同,A和C不同,那么这一位上B和C就相同)去掉两次(因为在前两次比较中各计算了一次),剩下的就是B和C的不同数目,很容易得到这样的关系式: ,从而三者不可能同为奇数。
,从而三者不可能同为奇数。
第三问,首先理解P中会出现 个距离,所以平均距离就是距离总和再除以
个距离,所以平均距离就是距离总和再除以 ,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来
,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来 一切就水到渠成了。
一切就水到渠成了。
此外,这个问题需要注意一下数学语言的书写规范。
解:(1)设
因 ,故
,故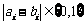 ,
, 即
即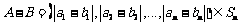
又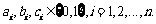 当
当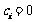 时,有
时,有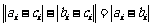 ;
;
当 时,有
时,有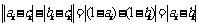 故
故
(2)设
记 记
记 ,由第一问可知:
,由第一问可知:



即 中1的个数为k,
中1的个数为k, 中1的个数为l,
中1的个数为l,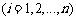
设t是使 成立的i的个数,则有
成立的i的个数,则有 ,
,
由此可知,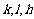 不可能全为奇数,即
不可能全为奇数,即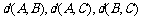 三个数中至少有一个是偶数。(3)显然P中会产生
三个数中至少有一个是偶数。(3)显然P中会产生 个距离,也就是说
个距离,也就是说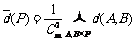 ,其中
,其中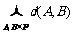 表示P中每两个元素距离的总和。分别考察第i个位置,不妨设P中第i个位置一共出现了
表示P中每两个元素距离的总和。分别考察第i个位置,不妨设P中第i个位置一共出现了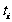 个1,
那么自然有
个1,
那么自然有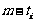 个0,因此在这个位置上所产生的距离总和为
个0,因此在这个位置上所产生的距离总和为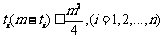 ,
,
那么n个位置的总和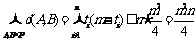 即
即
2.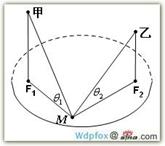 (2008年上海理10)某海域内有一孤岛,岛四周的海平面(视为平面)上有一浅水区(含边界),其边界是长轴长为2a,短轴长为2b的椭圆,已知岛上甲、乙导航灯的海拔高度分别为h1、h2,且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上,现有船只经过该海域(船只的大小忽略不计),在船上测得甲、乙导航灯的仰角分别为θ1、θ2,那么船只已进入该浅水区的判别条件是 .
(2008年上海理10)某海域内有一孤岛,岛四周的海平面(视为平面)上有一浅水区(含边界),其边界是长轴长为2a,短轴长为2b的椭圆,已知岛上甲、乙导航灯的海拔高度分别为h1、h2,且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上,现有船只经过该海域(船只的大小忽略不计),在船上测得甲、乙导航灯的仰角分别为θ1、θ2,那么船只已进入该浅水区的判别条件是 .
[答案]
[解析]依题意,
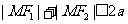
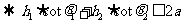 ;
;
1.(2010年北京理14)如图放置的边长为1的正方形PABC沿 轴滚动。设顶点P(
轴滚动。设顶点P( ,y)的轨迹方程是
,y)的轨迹方程是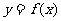 ,则
,则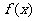 的最小正周期为
;
的最小正周期为
;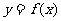 在其两个相邻零点间的图像与
在其两个相邻零点间的图像与 轴所围区域的面积为
。
轴所围区域的面积为
。
说明:“正方形PABC沿 轴滚动”包括沿
轴滚动”包括沿 轴正方向和沿
轴正方向和沿 轴负方向滚动。沿
轴负方向滚动。沿 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿 轴负方向滚动。
轴负方向滚动。
解析:不难想象,从某一个顶点(比如A)落在x轴上的时候开始计算,到下一次A点落在x轴上,这个过程中四个顶点依次落在了x轴上,而每两个顶点间距离为正方形的边长1,因此该函数的周期为4。下面考察P点的运动轨迹,不妨考察正方形向右滚动,P点从x轴上开始运动的时候,首先是围绕A点运动 个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:
个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:


因此不难算出这块的面积为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com