
1.钥匙与锁
一把坚实的大锁挂在大门上。钥匙来了,它瘦小的身子钻进锁孔,那大锁就啪的一声开了。铁棒奇怪的问:“为什么我费了那么大的力气也打不开,而你却轻而易举地打开了呢?” 钥匙说:“因为我最了解它的心啊!”
21.解:(1)当 ,
, 是增函数…1分,
是增函数…1分,
且 …………2分;
…………2分;
 ,
,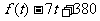 是减函数…………3分,
是减函数…………3分,
且 …………4分.
…………4分.
所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟…………5分.
(2) …………7分,
…………7分,
故讲课开始25分钟时,学生的注意力比讲课开始后5分钟更集中…………9分.
(3)当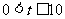 时,
时,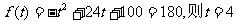 …………11分;
…………11分;
当 ,令
,令 …………12分,
…………12分,
则学生注意力在180以上所持续的时间28.57-4=24.57>24…………13分,
所以,经过适当安排,老师可以在学生达到所需要的状态下讲授完这道题…………14分.
20.解: (Ⅰ)∵ …………1分.
…………1分.
 在
在 上是增函数,在[0,3]上是减函数.
上是增函数,在[0,3]上是减函数.
∴ 当x=0时 取得极小值.∴
取得极小值.∴ . ∴b=0…………5分.
. ∴b=0…………5分.
∵方程 有三个实根, ∴a≠0…………6分.
有三个实根, ∴a≠0…………6分.
∴ =0的两根分别为
=0的两根分别为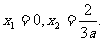 …………8分
…………8分
又 在
在 上是增函数,在[0,3]上是减函数.
上是增函数,在[0,3]上是减函数.
∴ 在
在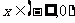 时恒成立,
时恒成立, 在
在 时恒成立…………10分.
时恒成立…………10分.
由二次函数的性质可知 …………13分.
…………13分.
∴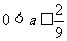 . 故实数
. 故实数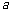 的取值范围为
的取值范围为 .…………14分
.…………14分
19.解:(Ⅰ)解法一:易知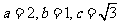 ,所以
,所以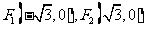 …………1分,设
…………1分,设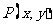 ,
,
则
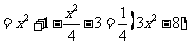 …………3分
…………3分
因为 ,故当
,故当 ,即点
,即点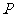 为椭圆短轴端点时,
为椭圆短轴端点时,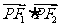 有最小值
有最小值 …………5分
…………5分
当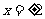 ,即点
,即点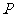 为椭圆长轴端点时,
为椭圆长轴端点时,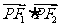 有最大值
有最大值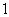 …………7分
…………7分
解法二:易知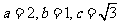 ,所以
,所以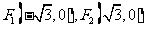 …………1分,设
…………1分,设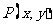 ,则
,则
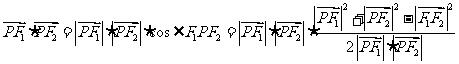
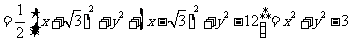 …………3分(以下同解法一)
…………3分(以下同解法一)
(Ⅱ)显然直线 不满足题设条件…………8分,
不满足题设条件…………8分,
可设直线 ,
,
联立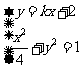 ,消2去
,消2去 ,整理得:
,整理得: …………9分
…………9分
由 >0
>0
得: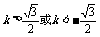 …………12分
…………12分
18.解法一
(I)直三棱柱ABC-A1B1C1中,CC1⊥平面ABC……1分
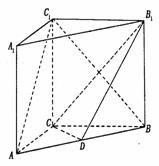 底面三边长AC=3,BC=4,AB=5,∴ AC⊥BC,……2分
底面三边长AC=3,BC=4,AB=5,∴ AC⊥BC,……2分
且BC1在平面ABC内的射影为BC,………….4分
∴ AC⊥BC1;……………….6分
 (II)设CB1与C1B的交点为E,连结DE,…………8分
(II)设CB1与C1B的交点为E,连结DE,…………8分
∵ D是AB的中点,E是BC1的中点,…………..10分
∴ DE//AC1,…………..11分
∵ DE 平面CDB1,AC1
平面CDB1,AC1 平面CDB1,………………………..13分
平面CDB1,………………………..13分
∴ AC1//平面CDB1;………………………….14分



 解法二:∵直三棱柱ABC-A1B1C1底面三边长AC=3,BC=4,AB=5,
解法二:∵直三棱柱ABC-A1B1C1底面三边长AC=3,BC=4,AB=5,
∴AC、BC、C1C两两垂直,……………2分
以C为坐标原点,直线CA、CB、C1C分别为x轴、y轴、z轴,
建立空间直角坐标系,……………3分
则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),
B1(0,4,4),D(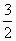 ,2,0)………
,2,0)………
(1)∵ =(-3,0,0),………4分
=(-3,0,0),………4分
 =(0,-4,0),………5分
=(0,-4,0),………5分
∴ •
• =0,……………6分
=0,……………6分
∴AC⊥BC1……………7分
(2)设CB1与C1B的交点为E,则E(0,2,2)……………8分
∵ =(-
=(-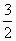 ,0,2),……………9分
,0,2),……………9分
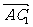 =(-3,0,4),……………10分
=(-3,0,4),……………10分
∴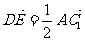 ,…………………11分
,…………………11分
∴DE∥AC1. …………………12分
DE 平面CDB1,AC1
平面CDB1,AC1 平面CDB1,………………………..13分
平面CDB1,………………………..13分
∴ AC1//平面CDB1;…………………………14分.
17.解:由 ,得
,得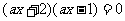 ……………………1分,
……………………1分,
显然 ……………………2分
……………………2分
所以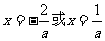 ,……………………3分
,……………………3分
因为方程 在
在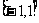 上有且仅有一解,故
上有且仅有一解,故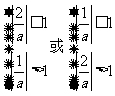 ……………………5分,
……………………5分,
所以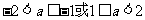 ……………………7分
……………………7分
只有一个实数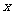 满足不等式
满足不等式 所以
所以 ……………………9分
……………………9分
因为命题 是假命题,所以命题p和命题q都是假命题……………………10分.
是假命题,所以命题p和命题q都是假命题……………………10分.
所以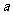 的取值范围为
的取值范围为 ……………………12分
……………………12分
16. 解:(1)当 时,
时,
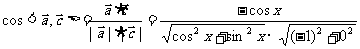 ………………2分
………………2分
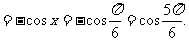 ………………3分
………………3分

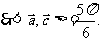 ……………………5分
……………………5分
(2) …………7分
…………7分

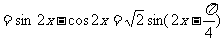 ……………………9分
……………………9分

 ……………………10分
……………………10分
故
∴当 ……………………12分
……………………12分
11. 12.①②③ 13.
12.①②③ 13.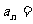 2n-4或
2n-4或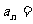 4-2n 14.
4-2n 14. 15. 700
15. 700
1.B 2.A 3.C 4.B 5.A 6.D 7.A 8.D 9.B 10.C
21.(本小题满分14分).通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f (t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知:

(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
广州市东风中学2010-2011年度高三综合训练(2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com