
2、 “达菲”是治疗甲型H1N1流感的一种药物,而合成达菲的主要原料莽草酸(化学式为C7H10O5)存在于我国盛产的八角茴香中。下列说法正确的是( )
A.莽草酸完全燃烧后的产物为CO2和H2O B.莽草酸中碳、氢元素质量比为7:10
C.莽草酸属于混合物 D.莽草酸由22个原子构成
1、2010年全国政协会议的“一号提案”是关于“低碳经济”。下列能量的获得过程中,不利于减少二氧化碳的排放且发生化学变化的是( )

A.太阳能路灯 B.燃煤取暖炉 C.水利发电站 D.风力发电站
15解(1):当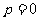 时,
时,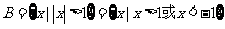 。。。。。。。。3分
。。。。。。。。3分
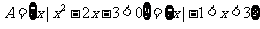 。。。。。。。。5分
。。。。。。。。5分
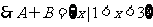 。。。。。。。。7分
。。。。。。。。7分
(2):由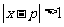 解得
解得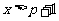 或
或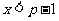
所以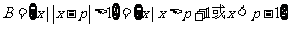 。。。。。。。。10分
。。。。。。。。10分
又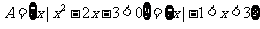
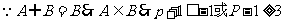
即 或
或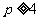 。。。。。。。。。。。。。14分
。。。。。。。。。。。。。14分
16解:(1)由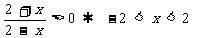
函数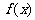 的定义域是
的定义域是 , 。。。。。。。。。。。。。。。。。。5分
, 。。。。。。。。。。。。。。。。。。5分
(2)由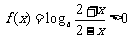
当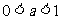 时,
时, 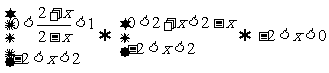 。。。。9分
。。。。9分
当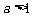 时,
时,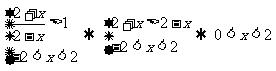 。。。。。。。。。。。。13分
。。。。。。。。。。。。13分
综上可知,当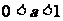 时
时 的取值范围是
的取值范围是
当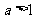 时
时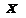 的取值范围是
的取值范围是 。。。。。。。。。。。14分
。。。。。。。。。。。14分
17解:(1)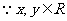 有
有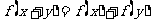
令 得
得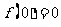 又令
又令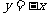 得
得
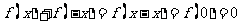
所以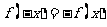 ,因此
,因此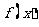 是R上的奇函数; 。。。。。。。。。。。。。。4分
是R上的奇函数; 。。。。。。。。。。。。。。4分
(2)设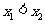 则
则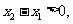
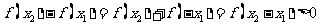
即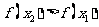 ,因此
,因此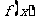 在
在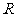 上为增函数; 。。。。。。。。。。。。。。。。9分
上为增函数; 。。。。。。。。。。。。。。。。9分
(3)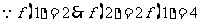 。。。。。。。。。。。。。。。11分
。。。。。。。。。。。。。。。11分
由 得
得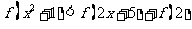
得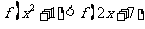 由(2)可得
由(2)可得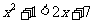
即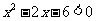 解得
解得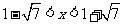 。。。。。。。。。。。。。。。。。14分
。。。。。。。。。。。。。。。。。14分
18解:(1)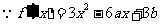 依题意知:
依题意知: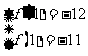
因此可得 解得
解得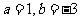 。。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。。7分
(2)由(1)知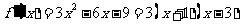
由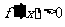 解得
解得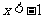 或
或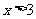 ,
,
因此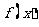 在
在 和
和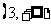 上为增函数;
上为增函数;
由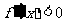 解得
解得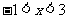 ,
,
因此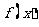 在
在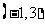 上为减函数。
。。。。。。。。。。。。。。。。14分
上为减函数。
。。。。。。。。。。。。。。。。14分
19解:(1)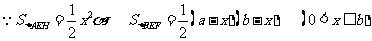

 。。。。。。。。。。。。。。。。。5分
。。。。。。。。。。。。。。。。。5分
(2)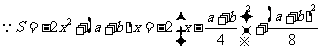 又
又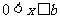
若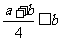 ,即
,即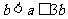 时,
时,
当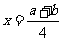 时,
时,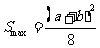 。。。。。。。。。。。。。。9分
。。。。。。。。。。。。。。9分
若 ,即
,即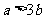 时,
时,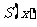 在
在 上为增函数,
上为增函数,
当 时,
时,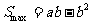 。。。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。。。12分
20解:(1) 恒成立,又
恒成立,又

解得 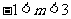 。。。。。。。。。。。。。。。。。5分
。。。。。。。。。。。。。。。。。5分
(2) 在区间
在区间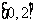 上有解,又
上有解,又
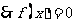 在区间
在区间 上有解
上有解
由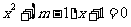 得
得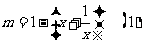 。。。。。。。。。。。。。。。8分
。。。。。。。。。。。。。。。8分
当 时,
时,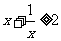 由(1)
由(1)
因此实数 的取值范围是:
的取值范围是: 。
。。。。。。。。。。。。。。。。12分
。
。。。。。。。。。。。。。。。。12分
13. 76 ; 14. 3。5 。
11.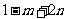 ; 12. 1 ;
; 12. 1 ;
20.(本题12分)关于二次函数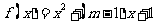
(1)若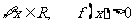 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(2)若方程 在区间
在区间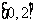 上有解,求实数
上有解,求实数 的取值范围。
的取值范围。
广州市东风中学2010-2011年度高三综合训练(3)
19.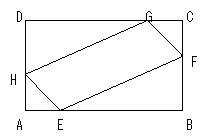 (本题12分)在矩形ABCD中,已知
(本题12分)在矩形ABCD中,已知
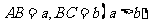 ,在AB、AD、CD、
,在AB、AD、CD、
CB上分别截取AE、AH、CG、CF都等于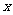 ,
,
(1)将四边形EFGH的面积S表示成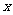 的函
的函
数,并写出函数的定义域;
(2)当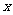 为何值时,四边形EFGH的面积最
为何值时,四边形EFGH的面积最
大?并求出最大面积。
18.(本题14分)设函数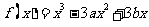 的图象与直线
的图象与直线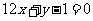 相切于点
相切于点
(1)求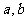 的值;(2)讨论函数
的值;(2)讨论函数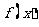 的单调性。
的单调性。
17.(本题14分)已知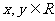 有
有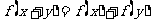
(1)判断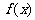 的奇偶性;
的奇偶性;
(2)若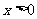 时,
时,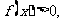 证明:
证明: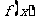 在
在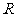 上为增函数;
上为增函数;
(3)在条件(1)下,若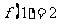 ,解不等式:
,解不等式:
16.(本题14分)已知函数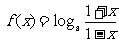 (
(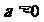 且
且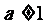 ),
),
(1)求 的定义域;
的定义域;
(2)求使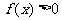 的
的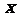 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com