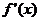
-

0

+

0

-

0

+

(1,+)

(-,-1)

-1

(-1,0)

0

(0,1)

1

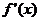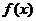、随x变化而变化情况如下：

向量（a-c）i-12bj=(a-c,-12b),故在x=2处的切线的斜率为，从而

解：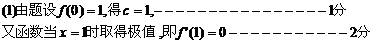

34. 已知向量i=(1,0),j=(0,1)，函数f(x)=ax⁴+bx²+c(a≠0，a≠c)的图象在y轴上的截距为1，在x=2处切线的方向向量为(a-c)i-12bj，并且函数当x=1时取得极值。

   （1）求f(x)的解析式；

   （2）求f(x)的单调递增区间和极值.