
即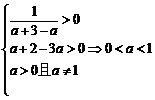
(2)f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上是接近的
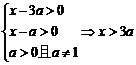
要使f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上有意义,
等价于真数的最小值大于0
28. 对于在区间[m,n]上有意义的两个函数f (x)与g (x),如果对任意x∈[m,n]均有| f
(x) ? g (x) |≤1,则称f (x)与g (x)在[m,n]上是接近的,否则称f (x)与g (x)在[m,n]上是非接近的,现有两个函数f 1(x)
= loga(x ? 3a)与f 2 (x)
= loga (a > 0,a≠1),给定区间[a
+ 2,a + 3].
(a > 0,a≠1),给定区间[a
+ 2,a + 3].
(1)若f 1(x)与f 2 (x)在给定区间[a + 2,a + 3]上都有意义,求a的取值范围;
(2)讨论f 1(x)与f 2 (x)在给定区间[a + 2,a + 3]上是否是接近的?
解:(1)要使f 1 (x)与f 2 (x)有意义,则有
(参考思路)在探求 时,要考虑以下因素:①
时,要考虑以下因素:① 在
在 上必须有意义(否则不能参加与
上必须有意义(否则不能参加与 的和运算);②由于
的和运算);②由于 和
和 都是以
都是以 为底的对数,所以构造的函数
为底的对数,所以构造的函数 可以是以
可以是以 为底的对数,这样与
为底的对数,这样与 和
和 进行的运算转化为真数的乘积运算;③以
进行的运算转化为真数的乘积运算;③以 为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去
为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去 ;⑤乘积的结果可以是
;⑤乘积的结果可以是 的二次函数,该二次函数的图像的对称轴应在直线
的二次函数,该二次函数的图像的对称轴应在直线 的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与
的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与 轴已有了一个公共点
轴已有了一个公共点 ,故对称轴又应该是
,故对称轴又应该是 轴或在
轴或在 轴的右侧(否则该二次函数的值在
轴的右侧(否则该二次函数的值在 上的值不能恒为正数),即若抛物线与
上的值不能恒为正数),即若抛物线与 轴的另一个公共点是
轴的另一个公共点是 ,则
,则 ,且抛物线开口向下.
,且抛物线开口向下.
∵ 在
在 单调递减, ∴
单调递减, ∴ 故
故  ,
,
即 有最小值
有最小值 ,但没有最大值.………………………18分
,但没有最大值.………………………18分
(其他答案请相应给分)
(3) ;或
;或 等. …………………15分
等. …………………15分
如:当 时,
时,
(根据函数 的单调性求得
的单调性求得 ,请相应给分)
,请相应给分)
(2)设 在
在 的图像上
的图像上
则 ,即
,即 ……………………………………8分
……………………………………8分
而 在
在 的图像上,∴
的图像上,∴
代入得, 为所求.…………………………………11分
为所求.…………………………………11分
解:(1)当点 坐标为(
坐标为( ),点
),点 的坐标为
的坐标为 ,…………2分
,…………2分
∵点 也在
也在 的图像上,∴
的图像上,∴ ,即
,即 .……5分
.……5分
 时有最小值而没有最大值.
时有最小值而没有最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com