
19.解析:(1)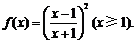
∵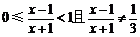 ,∴函数
,∴函数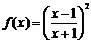 的值域为
的值域为
由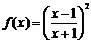 ,得
,得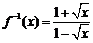 ,因此,函数
,因此,函数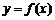 的反函数
的反函数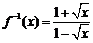
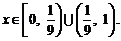
(2)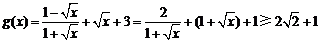 ,当且仅当
,当且仅当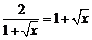 ,
,
即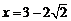 时,
时,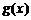 有最小值
有最小值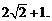
(3)由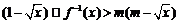 ,得
,得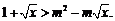
设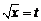 ,则
,则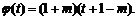
根据题意,对区间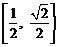 中的一切t值,
中的一切t值,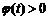 恒成立.
恒成立.
则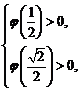 得
得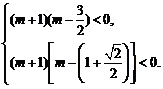 ∴
∴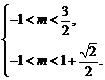
∴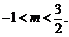 即实数m的取值范围是
即实数m的取值范围是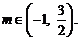
18.(1)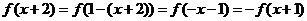
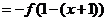
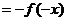
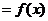 ,所以
,所以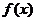 是周期为2的函数.
是周期为2的函数.
(2)∵当x∈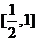 时,
时,  ,
,
∴x∈[0,1]时, 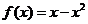
∴当x∈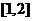 时,
时,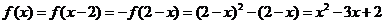 .
.
(3)由函数是以2为周期的函数,故只需要求出一个周期内的值域即可,由(2)知
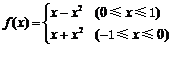 ,故在
,故在 上函数的值域是
上函数的值域是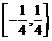 ,故值域为
,故值域为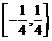
17.(1)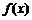 在
在 上是增函数,证明如下:
上是增函数,证明如下:
任取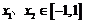 ,且
,且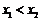 ,则
,则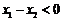 ,于是有
,于是有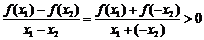 ,而
,而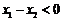 ,故
,故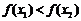 ,故
,故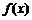 在
在 上是增函数
上是增函数
(2)由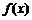 在
在 上是增函数知:
上是增函数知:
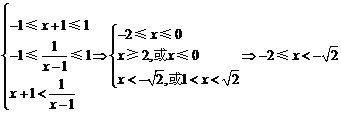 ,
,
故不等式的解集为 .
.
16. .(1)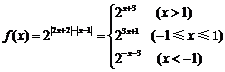 ,故函数的单增区间是
,故函数的单增区间是 ,
,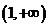 ;函数的减区间是
;函数的减区间是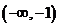
(2)由(1)知,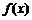 的最小值是
的最小值是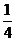 ,要
,要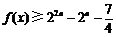 恒成立,则须
恒成立,则须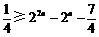 成立,解得,
成立,解得,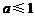
15. ①②③
20.(本小题满分13分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量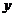 (升)关于行驶速度
(升)关于行驶速度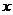 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为:
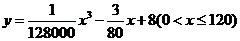 .已知甲、乙两地相距100千米
.已知甲、乙两地相距100千米
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
21(本小题满分14分)
已知函数f(x)=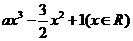 ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间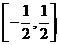 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
2011届曾都一中高三(文科)综合训练五
19.(本小题满分13分)已知函数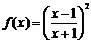 (其中x≥1且
(其中x≥1且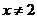 ).
).
(1)求函数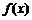 的反函数
的反函数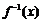 ;
;
(2)设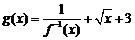 ,求函数
,求函数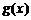 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式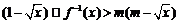 对于区间
对于区间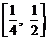 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.
18. (本题满分12分) 已知奇函数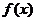 的定义域是R,且
的定义域是R,且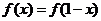 ,当0≤x≤
,当0≤x≤ 时,
时,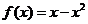 .
.
(1)求证: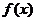 是周期为2的函数;
是周期为2的函数;
(2)求函数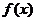 在区间
在区间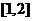 上的解析式;
上的解析式;
17.(本题满分12分)已知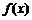 是定义在
是定义在 上的奇函数,若任意的
上的奇函数,若任意的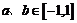 ,且
,且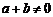 ,都有
,都有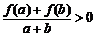 .
.
(1)判断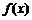 在
在 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(2)解不等式: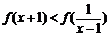 .
.
16.(本题满分12分)设函数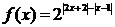 .
.
(1)求函数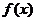 的单调区间;
的单调区间;
(2)若不等式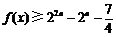 恒成立,求
恒成立,求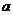 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com