
8.(天津十二区县重点中学2010年高三联考一理)两圆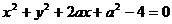 和
和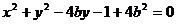 恰有三条公切线,若
恰有三条公切线,若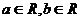 ,且
,且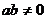 ,则
,则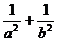 的最小值为
( C )[来源:高&考%资(源#网
的最小值为
( C )[来源:高&考%资(源#网
A.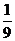 B.
B.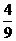 C.
C.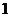 D.
D.
18. 解:(1)所有可能结果数为15.列举如下:
(1,1),(1,2),(1,3) ,(1,4),(1,5)
(2,1),(2,2),(2,3) ,(2,4),(2,5)
(3,1),(3,2),(3,3) ,(3,4),(3,5)
(4,1),(4,2),(4,3) ,(4,4),(4,5)
(5,1),(5,2),(5,3) ,(5,4),(5,5)
(2)取出球的号码之和不小于6的是:(1,5),(2,4),(2,5)(3,3),(3,4),(3,5)(4,2),(4,3),(4,4),(4,5)(5,1),(5,2),(5,3),(5,4),(5,5)共15种,
所以, .
.
(3)点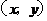 落在直线
落在直线
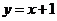 上方的有:(1,3),(1,4),(1,5),(2,4),(2,5),(3,5);共6种,
上方的有:(1,3),(1,4),(1,5),(2,4),(2,5),(3,5);共6种,
所以,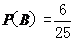 .
.
18.(天津市天津一中2010届高三第四次月考文科)一个盒子中装有5个编号依次为1、2、3、4、5的球,这5个球除号码外完全相同,有放回的连续抽取两次,每次任意地取出一个球.
(1)用列举法列出所有可能结果;
(2)求事件A=“取出球的号码之和不小于6”的概率;
(3)设第一次取出的球号码为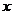 ,第二次取出的球号码为
,第二次取出的球号码为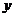 ,求事件B=“点(
,求事件B=“点(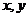 )落在直线
)落在直线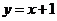 上方”的概率.
上方”的概率.
18、解:(Ⅰ)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡。设事件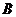 为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”, 事件
为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”, 事件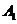 为“采访该团3人中,1人持金卡,0人持银卡”,
事件
为“采访该团3人中,1人持金卡,0人持银卡”,
事件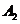 为“采访该团3人中,1人持金卡,1人持银卡”。
为“采访该团3人中,1人持金卡,1人持银卡”。
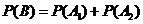 ……………………(2分)
……………………(2分)
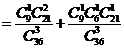
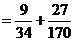 ……………………(4分)
……………………(4分)
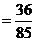
所以在该团中随机采访3人,恰有1人持金卡且持银卡者少于2人的概率是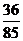 。
。
…………………………………………………………6分
(Ⅱ)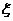 的可能取值为0,1,2,3
的可能取值为0,1,2,3
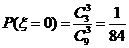 , ……………………(7分)
, ……………………(7分)
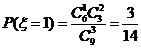 ……………………(8分)
……………………(8分)
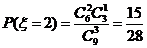 ,……………………(9分)
,……………………(9分)
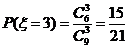 , ……………………(10分)
, ……………………(10分)
所以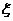 的分布列为
的分布列为
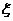 |
0 |
1 |
2 |
3 |
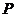 |
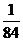 |
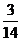 |
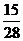 |
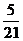 |
所以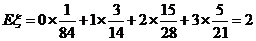 , ……………………12分
, ……………………12分
18.(天津市天津一中2010届高三第四次月考理科)为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司
组织了一个有36名游客的旅游团到四川名胜旅游,其中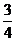 是省外游客,其余是省内游客。 在省外游客中有
是省外游客,其余是省内游客。 在省外游客中有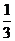 持金卡,在省内游客中有
持金卡,在省内游客中有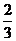 持银卡。
持银卡。
(I)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(II)在该团的省内游客中随机采访3名游客,设其中持银卡人数为随机变量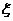 ,求
,求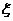 的分布列及数学期望
的分布列及数学期望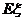 。
。
18.解:(I)记抽到的卡片标号为(x,y),所有的情况分别为,
|
(x,y) |
(1,1) |
(1,2) |
(1,3) |
(2,1) |
(2,2) |
(2,3) |
(3,1) |
(3,2) |
(3,3) |
|
P(x-2,x-y) |
(-1,0) |
(-1,-1) |
(-1,-2) |
(0,1) |
(0,0) |
(0,-1) |
(1,2) |
(1,1) |
(1,0) |
|
|OP| |
1 |
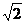 |
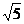 |
1 |
0 |
1 |
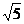 |
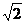 |
1 |
共9种.由表格可知|OP|的最大值为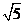 …………5分
…………5分
设事件A为“|OP|取到最大值”,则满足事件A的(x,y)有(1,3),(3,1)两种情况,
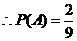 …………7分
…………7分
(II)设事件B为“P点在第一象限”
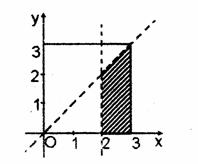 若
若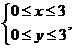 则其所表示的区域面积为
则其所表示的区域面积为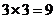
由题意可得事件B满足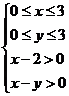 ,
,
即如图所示的阴影部分,
其区域面积为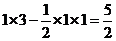
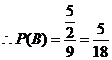 …………12分
…………12分
18.(天津市六校2010届高三第三次联考文科)(本小题满分12分)
设O为坐标原点,点P的坐标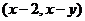
(I)在一个盒子中,放有标号为1,2,3的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为x,y,求|OP|的最大值,并求事件“|OP|取到最大值”的概率;
(II)若利用计算机随机在[0,3]上先后取两个数分别记为x,y,求P点在第一象限的概率.
18.解:若A研究所独立地研究“甲型H1N1流感”疫苗,则其经济效益的期望为
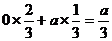 万元. …………3分
万元. …………3分
而两个研究所独立地研究时至少有一个研制成功的概率为
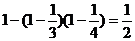 …………6分
…………6分
所以两个研究所合作研制成功的概率为
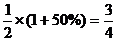 …………8分
…………8分
于是A研究所采用与B研究所合作的方式来研究疫苗,所获得的经济效益的期望为
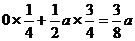 万元,而
万元,而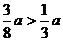 ,故应该建议A研究所采用与B研究所合作的方式来研究疫苗. …………12分
,故应该建议A研究所采用与B研究所合作的方式来研究疫苗. …………12分
18.(天津市六校2010届高三第三次联考理科)(本小题12分)
为预防“甲型H1N1流感”的扩散,某两个大国的研究所A、B均对其进行了研究.若独立地研究“甲型H1N1流感”疫苗,研究成功的概率分别为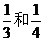 ;若资源共享,则提高了效率,即他们研究成功的概率比独立地研究时至少有一个研制成功的概率提高了50%.又疫苗研制成功获得经济效益a万元,而资源共享时所得的经济效益只能两个研究所平均分配.请你给A研究所参谋:是否应该采取与B研究所合作的方式来研究疫苗,并说明理由.
;若资源共享,则提高了效率,即他们研究成功的概率比独立地研究时至少有一个研制成功的概率提高了50%.又疫苗研制成功获得经济效益a万元,而资源共享时所得的经济效益只能两个研究所平均分配.请你给A研究所参谋:是否应该采取与B研究所合作的方式来研究疫苗,并说明理由.
18.(天津市武清区2009-2010学年高三下学期第一次模拟文)(本小题满分12分)
从1、2、3、4、5、8、9这7个数中任取三个数,共有35种不同的取法(两种取法不同,指的是一种取法中至少有一个数与另一种取法中的三个数都不相同)。
(1)求取出的三个数能够组成等比数列的概率;
(2)求取出的三个数的乘积能被2整除的概率。
解:(1)从1、2、3、4、5、8、9这7个数中任取三个数,每一种不同的取法为
一个基本事件,由题意可知共有35个基本事件。 …………………………………1分
设取出的三个数能组成等比数列的事件为A,A包含(1,2,4)、(2,4,8)、
(1,3,9)共3个基本事件。 ………………………………………………………6分
由于每个基本事件出现的可能性相等
所以,P(A)=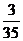 ……………………………………………………………7分
……………………………………………………………7分
(2)设取出的三个数的乘积能被2整除的事件为B,其对立事件为C,C包含
(1,3,5)、(1,3,9)、(1,5,9)、(3,5,9)共4个基本事件。 ……………9分
由于每个基本事件出现的可能性相等
所以,P(C)=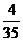 ………………………………………………………………11分
………………………………………………………………11分
所以,P(B)=1- P(C)=1-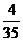 =
=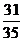 …………………………………………12分
…………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com