
1.下列各组物质的晶体中,化学键类型相同,晶体类型也相同的是
A.SiO2和SO2
B.CO2和H2O
C.NaCl和HCl
D.CCl4和KCl
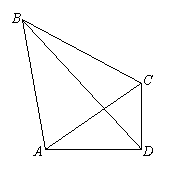
7.如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且 .
.
(1)求sin∠BAD的值;
(2)设△ABD的面积为S△ABD,△BCD的面积为S△BCD,求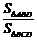 的值.
的值.
解 (1)在Rt△ADC中,AD=8,CD=6,
 则AC=10,
则AC=10,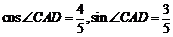 .
.
又∵ ,AB=13,
,AB=13,
∴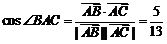 .
.
∵ ,∴
,∴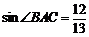 .
.
∴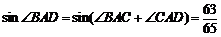 .
.
(2)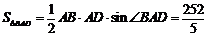 ,
,
 ,
, ,
,
则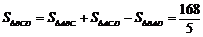 ,∴
,∴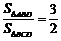 .
.
6.己知函数f(x)=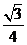 sin x一
sin x一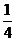 cos x。
cos x。
(1)若cosx=-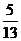 ,x
,x ,求函数f (x)的值;
,求函数f (x)的值;
(2)将函数f(x)的图像向右平移m个单位,使平移后的图像关于原点对称,
若0<m<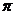 ,试求m的值。
,试求m的值。
解:(1)因为cos=-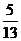 ,x
,x ,所以,sinx=
,所以,sinx=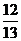
所以,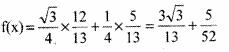
(2)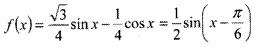 ,
,
所以,把f(x)的图象向右平移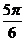 个单位,得到,y=-
个单位,得到,y=-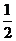 sinx的图象,其图象关于原点对称。
sinx的图象,其图象关于原点对称。
故m=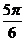
5.已知函数

 一个周期的图象如图所示,
一个周期的图象如图所示,
(1)求函数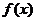 的表达式;
的表达式;
(2)若 ,且
,且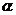 为
为 的一个内角,求
的一个内角,求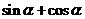 的值.
的值.
解:(1)从图知,函数的最大值为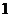 ,则
,则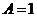
函数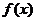 的周期为
的周期为 ,
,
而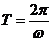 ,则
,则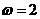 ,
,
又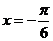 时,
时,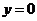 ,∴
,∴ ,
,
而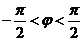 ,则
,则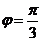 ,
,
∴函数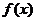 的表达式为
的表达式为 
(2)由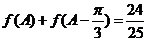 得:
得:
化简得: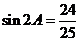 ,
,
∴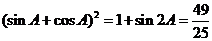
由于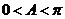 ,则
,则 ,
,
但 ,则
,则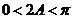 ,即A为锐角,
,即A为锐角,
从而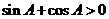
因此  .
.
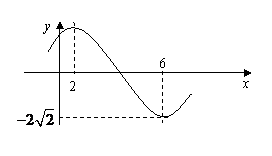
4.函数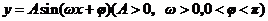 的图像一部分如图所示,
的图像一部分如图所示,
(1)求此函数解析式;
(2)将(1)中的函数图像如何变化才能得到函数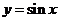 图像。
图像。
解:(1) 依题意知,
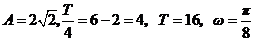 将点
将点 代入
代入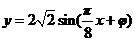 得
得 ,又
,又
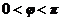 ,所以
,所以 ,所求函数解析式为
,所求函数解析式为 ;
;
(2)先把函数 的图像横坐标缩短为原来的
的图像横坐标缩短为原来的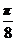 倍(纵坐标不变), 得函数
倍(纵坐标不变), 得函数 的图像,再把函数
的图像,再把函数 上所有点向右平移
上所有点向右平移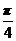 单位得到函数
单位得到函数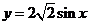 的图像,最后将
的图像,最后将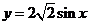 的图像上所有点的纵坐标缩短为原来的
的图像上所有点的纵坐标缩短为原来的 倍。
倍。
3.已知函数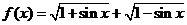 ,
,
(1)判断函数的奇偶性;(2)证明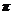 是函数的一个周期。
是函数的一个周期。
解:(1)定义域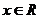 ,
,
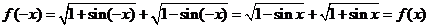 ,
,
所以函数为偶函数;
(2)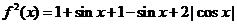 ,所以
,所以 ,
,
所以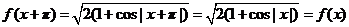 ,
,
所以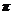 是函数的一个周期。
是函数的一个周期。
2.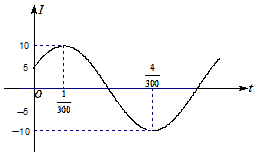 电流强度
电流强度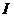 (安)随时间
(安)随时间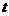 (秒)变化的函数
(秒)变化的函数
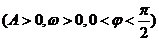 的图象如右图所示,则当
的图象如右图所示,则当 秒时,电流强度是
秒时,电流强度是
A.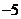 安
B.
安
B. 安
安
C.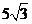 安 D.
安 D. 安
安
A
1.已知函数
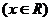 ,给出下列四个命题:
,给出下列四个命题:
①若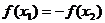 ,则
,则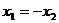 ②
②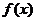 的最小正周期是
的最小正周期是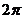
③在区间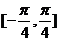 上是增函数 ④
上是增函数 ④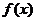 的图象关于直线
的图象关于直线 对称
对称
其中真命题是( )
 .①②④
.①②④  .①③
.①③  .②③
.②③  .③④
.③④
D
8.科网函数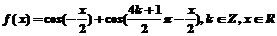 。
。
(1)求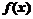 的周期;
的周期; 
(2)若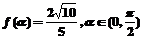 ,求
,求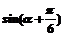 的值。
的值。
 解:(1)
解:(1)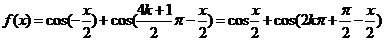
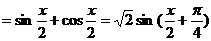 ,(
,(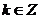 )
)
所以,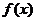 的周期
的周期 。
。
(2)由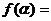
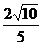 ,得
,得 ,
,
∴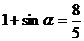 ,
∴
,
∴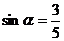
又 ,∴
,∴
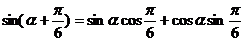 =
=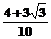
高考动车组3
三角函数2
l
正弦定理 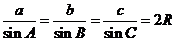 .
.
l
余弦定理 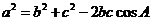 ;
;
l 面积定理
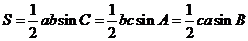
l 常见三角不等式
(1)若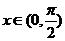 ,则
,则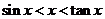 .(2) 若
.(2) 若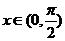 ,则
,则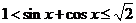 .
.
l
(3) 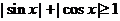
例1.已知偶函数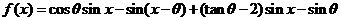 的最小值为0,求
的最小值为0,求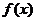 的最大值及此时x的集合。
的最大值及此时x的集合。
解: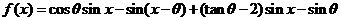
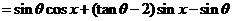 ,因为
,因为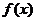 为偶函数,
为偶函数,
所以,对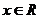 ,有
,有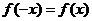 ,即
,即
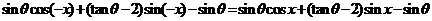 ,
,
亦即 ,所以
,所以 ,由
,由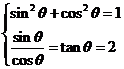 ,
,
解得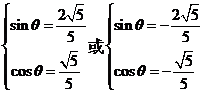 ,此时
,此时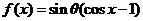 ,
,
当 时,
时,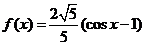 ,最大值为0,不合题意,
,最大值为0,不合题意,
当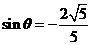 时,
时, ,最小值为0,
,最小值为0,
当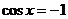 时,
时,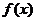 由最大值
由最大值 ,此时自变量x的集合为:
,此时自变量x的集合为:
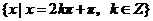 。
。
例2.已知函数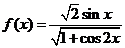 ,
,
(1)求函数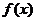 的定义域、值域、最小正周期;
的定义域、值域、最小正周期;
(2)判断函数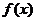 奇偶性。
奇偶性。
解:(1)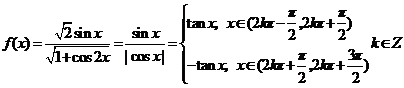 ,
,
定义域: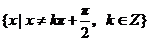 ,值域为:R,最小正周期为
,值域为:R,最小正周期为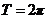 ;
;
(2) 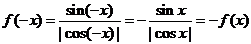 ,且定义域关于原点对称,
,且定义域关于原点对称,
所以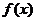 为奇函数。
为奇函数。
例3.已知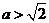 ,求
,求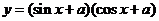 的最值。
的最值。
解: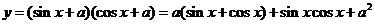 ,
,
令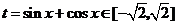 ,则有
,则有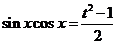 ,
,
所以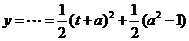 ,因为
,因为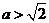 ,则
,则
当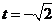 时,
时, ,当
,当 时,
时,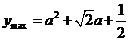 。
。
例4.已知函数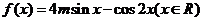 ,若函数
,若函数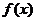 的最大值为3,求实数m的值。
的最大值为3,求实数m的值。
解: ,
,
令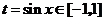 ,则函数变为
,则函数变为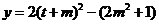 ,分类讨论如下:
,分类讨论如下:
(1)当 时,在t=1时,
时,在t=1时,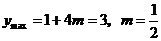 ;
;
(2)当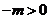 时,在t=-1时,
时,在t=-1时, ;
;
综上所述,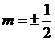 。
。
作业
7.已知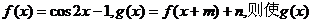 为奇函数的实数m,n的可能取值为( D
)
为奇函数的实数m,n的可能取值为( D
)
A. B.
B.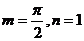
C.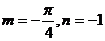 D.
D.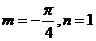
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com