
7、下列关于放射线的说法中正确的是:
A、放射线可以用来进行工业探伤
B、放射线可以使细胞发生变异
C、放射性同位素可以用来做示踪原子
D、放射线对人体无害
6、一颗子弹水平射入置于光滑水平面上的木块,并留在其中,A、B用一根弹性良好的轻质弹簧连在一起,如图所示,则在子弹打中木块A及弹簧被压缩的整个过程中,对子弹、两木块和弹簧组成的系统
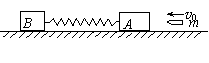 A.动量守恒、机械能守恒
A.动量守恒、机械能守恒
B.动量不守恒、机械能守恒
C.动量守恒、机械能不守恒
D.无法判断动量、机械能是否守恒
5、一物体做匀加速直线运动,在第一个ts内的位移为x1,在第二个ts内的位移为x2,则物体在第一个ts末的速度是
A、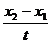 B、
B、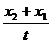
C、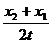 D、
D、
4、下列说法中正确的是
A、振荡电流就是一种频率很高的交流电;
B、LC振荡电路中,当电容器放电完毕时,线圈中的电流为零;
C、LC振荡电路中,电容器的充电过程就是磁场能向电场能转化的过程;
D、在振荡过程中线圈中的自感现象总是阻碍线圈中电流的变化。
3、光在某种玻璃中的传播速度是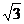 ×108m/s,要使光由玻璃射入空气时折射光线与反射光线成直角,则入射角应是
×108m/s,要使光由玻璃射入空气时折射光线与反射光线成直角,则入射角应是
A、30° B、60° C、45° D、90°
2、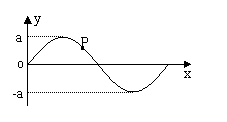 简谐横波某时刻的波形如图示,P为介质中的
简谐横波某时刻的波形如图示,P为介质中的
一个质点,以下说法正确的是
A、经过一个周期,质点P经过的路程为4a。
B、再过半个周期时,质点P的位移为负值:
C、若波沿x轴正方向传播,则质点P此时刻的加速度沿y轴正方向:
D、若波沿x轴正方向传播,则质点P此时刻的速度沿x轴正方向:
1.关于波长的下列说法中正确的是
A.在一个周期内振动在介质中传播的距离等于波长
B.在一个周期内介质的质点所走过的路程等于波长
C.在波的传播方向上位移相同的两相邻的质点间的距离是一个波长
D、对平衡位置的位移始终相同的质点间距离是一个波长
19. (本小题满分13分) 已知函数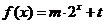 的图象经过点A(1,1),B(2,3) ,及C(n,Sn),Sn为数列
的图象经过点A(1,1),B(2,3) ,及C(n,Sn),Sn为数列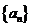 的前n项的和,
的前n项的和, (1) 求Sn及an (2)
设bn=log2an-1,数列
(1) 求Sn及an (2)
设bn=log2an-1,数列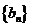 的前n项和为Tn ,求证:
的前n项和为Tn ,求证: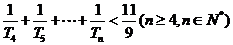
解 (1)由 2m+t=1得 t= -1
4m+t=3 m=1 2分
所以 f(x)=2x -1 则 Sn=2n -1  4分
4分
当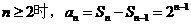
当n=1时,a1=S1=1满足上式,所以an=2n-1 ( )
6 分
)
6 分
(2)证明:因为bn=log2an-1=n-2
所以 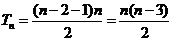 8分
8分
所以 ,当n≥4时,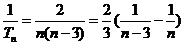 10分
10分
所以 13分
13分
20(本小题满分13分)
在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的长方体无盖容器(只有一个下底面和侧面的长方体).该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求的方案,简单说明操作过程和理由.
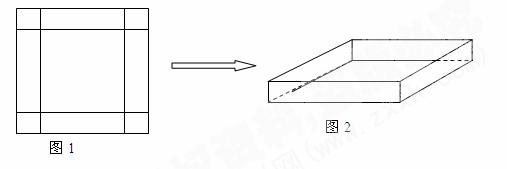
解:(1)设切去正方形边长为x,则焊接成的长方体的底面边长为4-2x,高为x ,
所以V1= (4-2x)2·x = 4(x3-4x2 + 4x) (0<x<2) .……….. ……….. ……….. 4分
∴V1/ = 4(3x2-8x + 4),……….. ……….. ……….. ……….. ……….. ………. ….5分
令V1/ = 0,即4(3x2-8x + 4) = 0,解得x1 = ,x2 = 2 (舍去) .……….. ………7分
∵ V1在(0,2)内只有一个极值,
∴ 当x = 时,V1取得最大值.<5,即不符合要求. ….…. …. 9分
(2)重新设计方案如下:
如图①,在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;如图③,将图②焊成长方体容器.新焊长方体容器底面是一个长方形,长为3,宽为2,此长方体容积V2 = 3×2×1 = 6,显然V2>5.
故第二种方案符合要求.
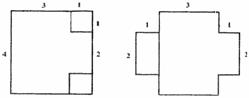
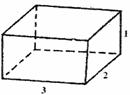
图① 图② 图③
…. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. …. ….13分
注:第二问答案不唯一。
21(本小题满分13分)
已知函数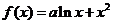 (为实常数).
(为实常数).
(Ⅰ) 若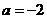 ,求证:函数
,求证:函数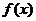 在
在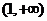 上是增函数;
上是增函数;
(Ⅱ) 若存在x∈[1,e],使得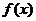 ≤
≤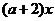 成立,求实数的取值范围.
成立,求实数的取值范围.
(Ⅲ) 求函数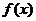 在[1,e]上的最小值及相应的x值;
在[1,e]上的最小值及相应的x值;
解:(Ⅰ)当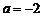 时,
时, ,当
,当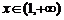 ,
, ,
,
故函数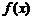 在
在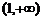 上是增函数.………………………………………………………………………2分
上是增函数.………………………………………………………………………2分
(Ⅱ) 不等式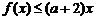 , 可化为
, 可化为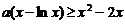 .∵
.∵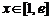 ,
,
∴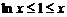 且等号不能同时取,所以
且等号不能同时取,所以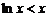 ,即
,即 ,因而
,因而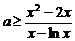 (
(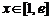 )… 4 分
)… 4 分
令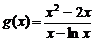 (
(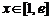 ),又
),又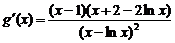 ……………………………………
……………………………………
当 时,
时,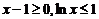 ,
,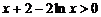 ,…………………………………………………6分
,…………………………………………………6分
从而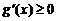 (仅当x=1时取等号),所以
(仅当x=1时取等号),所以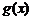 在
在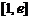 上为增函数 ………………………………
上为增函数 ………………………………
故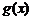 的最小值为
的最小值为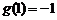 ,所以实数的取值范围是
,所以实数的取值范围是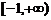 ……………………………………8分
……………………………………8分
(Ⅲ) 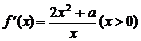 ,当
,当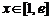 ,
, .………………………………
.………………………………
若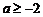 ,
,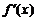 在
在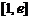 上非负(仅当
上非负(仅当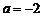 ,
,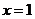 时,
时,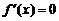 ),故函数
),故函数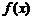 在
在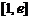 上是增函数,此时
上是增函数,此时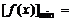
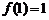 . …………………………………………9分
. …………………………………………9分
若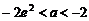 ,当
,当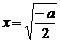 时,
时,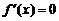 ;当
;当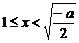 时,
时,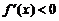 ,此时
,此时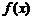 是减函数; 当
是减函数; 当 时,
时,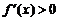 ,此时
,此时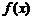 是增函数.故
是增函数.故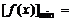
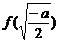
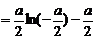 … 11…分
… 11…分
若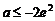 ,
,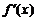 在
在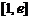 上非正(仅当
上非正(仅当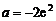 ,
,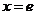 时,
时,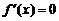 ),故函数
),故函数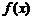 在
在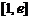 上是减函数,此时
上是减函数,此时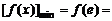
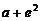 . …………………………………………………………12分…
. …………………………………………………………12分…
综上可知,当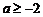 时,
时,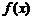 的最小值为1,相应的x值为1;
的最小值为1,相应的x值为1;
当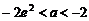 时,
时,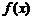 的最小值为
的最小值为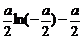 ,相应的x值为
,相应的x值为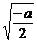 ;
;
当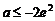 时,
时,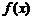 的最小值为
的最小值为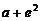 ,相应的值为……………………………………………13分
,相应的值为……………………………………………13分
18. 在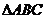 中,内角A、B、C对边的边长分别是a、b、c,已知c=2,
中,内角A、B、C对边的边长分别是a、b、c,已知c=2,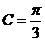
(1)若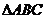 的面积等于
的面积等于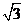 ,求a、b;(2)若sinC+sin(B-A)=2sin2A,求
,求a、b;(2)若sinC+sin(B-A)=2sin2A,求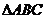 的面积
的面积
解
由余弦定理及已知条件得 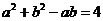 ①
2分
①
2分
又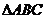 面积
面积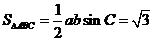 得ab=4
②
4分
得ab=4
②
4分
由①②得a=2,b=2 6分
(2) 由题意得sin(B+A)+sin(B-A)=4sinAcosA
即 sinB cosA=2sinAcosA 8分
当cosA=0时,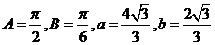 10分
10分
当cosA≠0时,将sinB =2sinA,由正弦定理得b=2a与①联立解得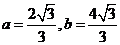
所以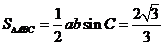 12分
12分
16 (本题满分12分)
已知向量m=(cosθ,sinθ)和n=( -sinθ,cosθ),θ∈[π,2π].
-sinθ,cosθ),θ∈[π,2π].
(1)求|m+n|的最大值;
(2)当|m+n|=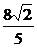 时,求cos(
时,求cos(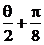 )的值.
)的值.
解:(1)m+n=(cosθ-sinθ+ ,cosθ+sinθ),
,cosθ+sinθ),
|m+n|=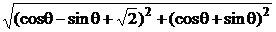
= 2分
2分
=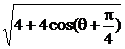
=2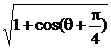 4分
4分
∵θ∈[π,2π],∴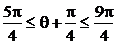 ,∴cos(θ+
,∴cos(θ+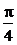 )≤1,|m+n|max=2
)≤1,|m+n|max=2 .
6分
.
6分
(2)由已知|m+n|=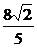 ,得cos(θ+
,得cos(θ+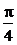 )=
)=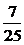 .
8分
.
8分
又cos(θ+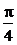 )=2cos2(
)=2cos2(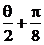 )-1,∴cos2(
)-1,∴cos2(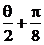 )=
)=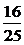 ,
10分
,
10分
∵θ∈[π,2π],∴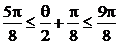 ,∴cos(
,∴cos(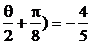 .
12分
.
12分
17.(本小题满分12分)
已知命题:“函数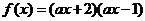 在
在 上存在零点”;
命题
上存在零点”;
命题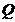 :“只有一个实数满足不等式
:“只有一个实数满足不等式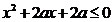 ”,若命题或
”,若命题或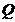 是假命题,求实数的取值范围.
是假命题,求实数的取值范围.
解:函数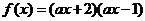 在
在 上存在零点
上存在零点
∴方程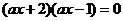 有解
有解
显然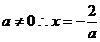 或
或 ……………………………………2分
……………………………………2分
∵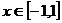 ,故
,故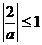 或
或
∴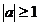 ……………………………………4分
……………………………………4分
只有一个实数满足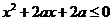 即抛物线
即抛物线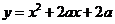 与x轴只有一个交点
与x轴只有一个交点
∴ 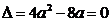
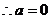 或
或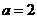 ……………………………………8分
……………………………………8分
∴命题或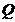 为真命题时,
为真命题时,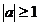 或
或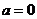
∵命题或 为假命题
为假命题
∴的取值范围为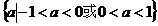 ……………………………………12分
……………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com