
8.设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
t |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωx+φ)的图象,下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
A.y=12+3sint,t∈[0,24]
B.y=12+3sin(t+π),t∈[0,24]
C.y=12+3sint,t∈[0,24]
D.y=12+3sin(t+),t∈[0,24]
解析:代入坐标验证即可选A.
答案:A
|
题组四 |
函数y=Asin(ωx+φ)的综合应用 |
7.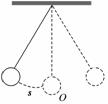 如图,单摆从某点开始来回摆动,离开平衡位置O的距离
如图,单摆从某点开始来回摆动,离开平衡位置O的距离
s cm和时间t s的函数关系式为s=6sin(2πt+),那么单摆
来回摆动一次所需的时间为 ( )
A.2π s B.π s
C.0.5 s D.1 s
解析:T==1,∴选D.
答案:D
6.(2010·黄冈模拟)已知函数f(x)=Acos(ωx+φ)的图角如图所示,f()=-,则f(0)=________.
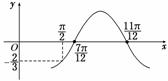
解析:由图象可得最小正周期为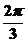 .
.
所以f(0)=f(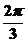 ),注意到
),注意到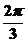 与
与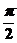 关于
关于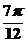 对称,
对称,
故f(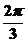 )=-f(
)=-f(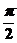 )=
)=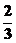 .
.
答案: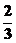
|
题组三 |
三角函数模型的应用 |
5.(2009·江苏高考)函数y=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)在闭区间[-π,0]上的图象如图所示,则ω=________.
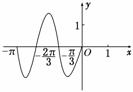
解析:由图中可以看出:
T=π,∴T=π=,
∴ω=3.
答案:3
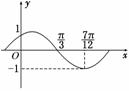
4.把函数y=sin(ωx+φ)(ω>0,|φ|<)的图象向左平移个单位长度,所得的曲线的一部分图象如图所示,则ω、φ的值分别是 ( )
A.1,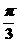 B.1,-
B.1,-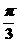
C.2,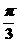 D.2,-
D.2,-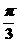
解析:y=sin(ωx+φ) 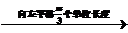
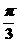 y1=sin[ω(x+
y1=sin[ω(x+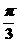 )+φ],∴T=
)+φ],∴T=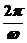 =
= 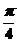 ×4,ω=2,当x=
×4,ω=2,当x=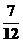 π时,2(
π时,2(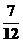 π+
π+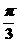 )+φ=2kπ+
)+φ=2kπ+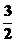 π,k∈Z,φ=2kπ-
π,k∈Z,φ=2kπ-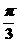 ,k∈Z,|φ|<
,k∈Z,|φ|<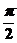 ,∴φ=-
,∴φ=-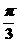 .
.
答案:D
3.已知函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,则ω=________.
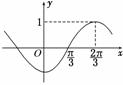
解析:由题意设函数周期为T,则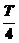 =
=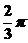 -
-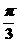 =
=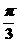 ,
,
∴T=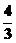 π,
π,
∴ω=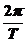 =
=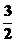 .
.
答案: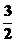
|
题组二 |
求三角函数y=Asin(ωx+φ)的解析式 |
2.(2009·全国卷Ⅱ)若将函数y=tan(ωx+)(ω>0)的图象向右平移个单位长度后,与函数y=tan(ωx+)的图象重合,则ω的最小值为 ( )
A. B. C. D.
解析:y=tan(ωx+)向右平移个单位长度后得到函数解析式y=tan,即y=tan(ωx+-),显然当-=+kπ时,两图象重合,此时ω=-6k(k∈Z).
∵ω>0,∴k=0时,ω的最小值为.
答案:D
1.(2009·天津高考)已知函数f(x)=sin(ωx+)(x∈R,ω>0)的最小正周期为π.将y=f(x)的图象向左平移|φ|个单位长度,所得图象关于y轴对称,则φ的一个值是 ( )
A. B. C. D.
解析:∵=π,∴ω=2,∴f(x)=sin(2x+),将它向左平移|φ|个单位长度,得f(x)=sin[2(x+|φ|)+],
∵它的图象关于y轴对称,
∴2(0+|φ|)+=+kπ.
∴φ=+,k∈Z.
∴φ的一个值是.
答案:D
11.已知f(x)=sin(ωx+)(ω>0),f()=f(),且f(x)在区间(,)有最小值,无最大值,则ω=________.
解析:由f()=f(),
知f(x)的图像关于x=对称.且在x=处有最小值,
∴ω+=2kπ-,
有ω=8k-(k∈Z).
又∵T=>-=,
∴ω<6,
故k=1,ω=.
10.(2009·福建四地六校联考)若函数f(x)同时满足下列三个性质:①最小正周期为π;②图象关于直线x=对称;③在区间[-,]上是增函数.则y=f(x)的解析式可以是 ( )
A.y=sin(2x-) B.y=sin(+)
C.y=cos(2x-) D.y=cos(2x+)
解析:逐一验证,由函数f(x) 的周期为π,故排除B;
又∵cos(2×-)=cos=0,故y=cos(2x-)的图象不关于直线x=对称;
令-+2kπ≤2x-≤+2kπ,得-+kπ≤x≤+kπ,k∈Z,
∴函数y=sin(2x-)在[-,]上是增函数.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com