1.(2009·广东高考)已知△ABC中，∠A，∠B，∠C的对边分别为a，b，c.若a＝c＝+，且∠A＝75°，则b＝　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．2 　　　B．4+2　　　　 C．4－2　 　　　D.－

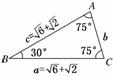解析：如图所示．

在△ABC中，由正弦定理得

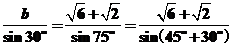=4，

∴b=2.

答案：A

3．在△ABC中，已知cos(+A)＝，则cos2A的值为________．

解析：cos(+A)＝coscosA－sinsinA

＝(cosA－sinA)＝，

∴cosA－sinA＝＞0.　　　　　　　　　　　　　　　　　　　　　　　　 ①

∴0＜A＜，∴0＜2A＜

①²得1－sin2A＝，∴sin2A＝.

∴cos2A＝＝.

2．(2010·平顶山模拟)在△ABC中，sin²A+cos²B＝1，则cosA+cosB+cosC的最大值为(　)

A.　 　　　B.　 　　　C．1 　　　　D.

解析：由sin²A+cos²B＝1，得sin²A＝sin²B，

∴A＝B，故cosA+cosB+cosC＝2cosA－cos2A

＝－cos²A+2cosA+1.

又0＜A＜，0＜cosA＜1.

∴cosA＝时，有最大值.

答案：D

1.如果α∈(，π)，且sinα＝，那么sin(α+)+cos(α+)＝　　　　　　　　　　 (　)

A.　 　　B．－　　　 C.　 　　D．－

解析：∵sinα＝，＜α＜π，∴cosα＝－，而sin(α+)+cos(α+)＝sin(α+)＝　　

cosα＝－.

答案：D

12．(文)已知点M(1+cos2x,1)，N(1，sin2x+a)(x∈R，a∈R，a是常数)，设y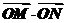＝ (O为坐标原点)．

(1)求y关于x的函数关系式y＝f(x)，并求f(x)的最小正周期；

(2)若x∈[0，]时，f(x)的最大值为4，求a的值，并求f(x)在[0，]上的最小值．

解：(1)依题意得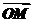：＝(1+cos2x,1)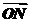，＝(1，sin2x+a)，

∴y＝1+cos2x+sin2x+a＝2sin(2x+)+1+a.

∴f(x)的最小正周期为π.

(2)若x∈[0，]，则(2x+)∈[，]，

∴－≤sin(2x+)≤1，

此时y_max＝2+1+a＝4，∴a＝1，

y_min＝－1+1+1＝1.

(理)已知α、β为锐角，向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，c＝(，－)．

(1)若a·b＝，a·c＝，求角2β－α的值；

(2)若a＝b+c，求tanα的值．

解：(1)∵a·b＝(cosα，sinα)·(cosβ，sinβ)

＝cosαcosβ+sinαsinβ

＝cos(α－β)＝，　　　　　　　　　　　　　　　　　　　　　　 ①

a·c＝(cosα，sinα)·(，－)

＝cosα－sinα＝，　　　　　　　　　　　　　　　　　　　 ②

又∵0＜α＜，0＜β＜，

∴－＜α－β＜.

由①得α－β＝±，由②得α＝.

由α、β为锐角，∴β＝.

从而2β－α＝π.

(2)由a＝b+c可得

③²+④²得cosα－sinα＝，

∴2sinαcosα＝.

又∵2sinαcosα＝

＝＝，

∴3tan²α－8tanα+3＝0.

又∵α为锐角，∴tanα＞0，

∴tanα＝

＝

＝.

11．已知cos(α－)+sinα＝，则sin(α+)的值为________．

解析：∵cos(α－)+sinα＝cosα+sinα＝，

∴cosα+sinα＝，

∴sin(α+)＝－sin(α+)＝－(sinα+cosα)

＝－.

答案：－

10.(2010·晋城模拟)已知向量a＝(sin(α+),1)，b＝(4,4cosα－)，若a⊥b，则sin(α+)等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－ 　　　　　B．－　　　　　 C. 　　　　　D.

解析：a·b＝4sin(α+)+4cosα－

＝2sinα+6cosα－＝4sin(α+)－＝0，

∴sin(α+)＝.

∴sin(α+)＝－sin(α+)＝－.

答案：B

9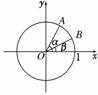．如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α、β，它们的终边分别

与单位圆相交于A、B两点．已知A、B的横坐标分别为，.

(1)求tan(α+β)的值；

(2)求α+2β的值．

解：(1)由已知条件及三角函数的定义可知，cosα＝，cosβ＝.因α为锐角，故sinα　　　

＞0，从而sinα＝＝，同理可得sinβ＝.因此tanα＝7，tanβ＝.

所以tan(α+β)＝＝＝－3.

(2)tan(α+2β)＝tan[(α+β)+β]＝＝－1.

又0＜α＜，0＜β＜，故0＜α+2β＜，

从而由tan(α+2β)＝－1得α+2β＝.

8．在△ABC中，3sinA+4cosB＝6,4sinB+3cosA＝1，则C等于　　　　 (　)

A．30° 　　B．150°　 C．30°或150° 　　D．60°或120°

解析：已知两式两边分别平方相加，得

25+24(sinAcosB+cosAsinB)＝25+24sin(A+B)＝37，

∴sin(A+B)＝sinC＝，∴C＝30°或150°.

当C＝150°时，A+B＝30°，此时3sinA+4cosB＜3sin30°+4cos0°＝，这与3sinA+4cosB＝6相矛盾，∴C＝30°.

答案：A

7.已知A、B均为钝角，且sinA＝，sinB＝，则A+B等于　　　　　　　　　 (　)

A.　 　　　B.　　　 C.或 　　　D.

解析：由已知可得cosA＝－，cosB＝－，

∴cos(A+B)＝cosAcosB－sinAsinB＝，

又∵＜A＜π，＜B＜π，

∴π＜A+B＜2π，∴A+B＝.

答案：B