
1 证明下列不等式:
证明下列不等式:
(1)a,b∈R,求证|a+b|≤|a|+|b|;
(2)已知|h|< ,|k|<
,|k|< (ε>0),求证:|hk|<ε;
(ε>0),求证:|hk|<ε;
(3)已知|h|<cε, c <|x| (c>0,ε>0),求证:| |<ε
|<ε
分析:用绝对值性质及不等式性质作推理运算 绝对值性质有:
绝对值性质有:
|ab|=|a|·|b|;|an|=|a|n,| |=
|= 等
等
证明:(1)证法1:∵-|a|≤a≤|a|,-|b|≤b≤|b|
∴-(|a|+|b|)≤a+b≤|a|+|b| 即|a+b|≤|a|+|b|
证法2:(平方作差)(|a|+|b|)2-|a+b|2=a2+2|a||b|+b2-(a2+2ab+b2)
=2[|a|·|b|-ab)=2(|ab|-ab)≥0显然成立 故(|a|+|b|)2≥|a+b|2
故(|a|+|b|)2≥|a+b|2
又∵|a|+|b|≥0,|a+b|≥0,所以|a|+|b|≥|a+b|, 即|a+b|≤|a|+|b|
(2)∵0≤|h|< ,0≤|k|<
,0≤|k|< (ε>0),∴0≤|hk|=|h|·|k|<
(ε>0),∴0≤|hk|=|h|·|k|< ·
· =ε
=ε
(3)由0<c<|x|可知:
0< 且0≤|h|<cε,∴
且0≤|h|<cε,∴ ·cε,即|
·cε,即| |<ε
|<ε
2 求证:|x+
求证:|x+ |≥2(x≠0)
|≥2(x≠0)
分析:x与 同号,因此有|x+
同号,因此有|x+ |=|x|+|
|=|x|+| |
|
证法一:∵x与 同号,∴|x+
同号,∴|x+ |=|x|+
|=|x|+
∴|x+ |=|x|+
|=|x|+ ≥2
≥2 =2,即|x+
=2,即|x+ |≥2
|≥2
证法二:当x>0时,x+ ≥2
≥2 =2
=2
当x<0时,-x>0,有
-x+
∴x∈R且x≠0时有x+ ≤-2,或x+
≤-2,或x+ ≥2
≥2
即|x+ |≥2
|≥2
方法点拨:不少同学这样解:
因为|x+ |≤|x|+
|≤|x|+ ,又|x|+
,又|x|+ ≥2
≥2 =2,所以|x+
=2,所以|x+ |≥2
|≥2
学生认为这样解答是根据不等式的传递性 实际上,上述两个不等式是异向不等式,是不符合传递性的,因而如此作解是错误的
实际上,上述两个不等式是异向不等式,是不符合传递性的,因而如此作解是错误的
3 已知:|A-a|<
已知:|A-a|< ,|B-b|<
,|B-b|< ,求证:
,求证:
(1)|(A+B)-(a+b)|<ε;(2)|(A-B)-(a-b)|<ε
分析:证明本题的关键是把结论的左边凑出条件的左边,创造利用条件的机会
证明:因为|A-a|< ,|B-b|<
,|B-b|<

所以(1)|(A+B)-(a+b)|=|(A-a)+(B-b)|≤|A-a|+|B-b|< +
+ =ε
=ε
即|(A+B)-(a+b)|<ε
(2)|(A-B)-(a-b)|=|(A-a)-(B-b)|≤|A-a|+|B-b|< +
+ =ε
=ε
即|(A-B)-(a-b)|<ε
方法点拨:本题的证明过程中运用了凑的技巧,望给予足够重视,灵活掌握
已知:|x-1|≤1,
求证:(1)|2x+3|≤7; (2)|x2-1|≤3
证明:(1)∵|2x+3|=|2(x-1)+5|≤2|x-1|+5≤2+5=7
(2)|x2-1|=|(x+1)(x-1)|=|(x-1)[(x-1)+2]|
≤|x-1||(x-1)+2|≤|x-1|+2≤1+2=3
例1 已知|x|< ,|y|<
,|y|< ,|z|<
,|z|< , 求证 |x+2y-3z|<ε
, 求证 |x+2y-3z|<ε
证明:|x+2y-3z|≤|x|+|2y|+|-3z|=|x|+2|y|+3|z|
∵|x|< ,|y|<
,|y|< ,|z|<
,|z|< ,
,
∴|x|+2|y|+3|z|<
∴|x+2y-3z|<ε
说明:此例题主要应用了推论1,其中出现的字母ε,其目的是为学生以后学习微积分作点准备
例2 设a, b, c, d都是不等于0的实数,求证 ≥4
≥4
证明:∵ 
∴ ①
①
 ②
②
又  ③
③
由①,②,③式,得

说明:此题作为一个含绝对值的不等式,在证明过程中运用了基本不等式及不等式的性质,在证法上采用的是综合法
例3
已知|a|<1,|b|<1,求证 <1
<1
证明: <1
<1 <1
<1

由|a|<1,|b|<1,可知(1-a2)(1-b2)>0成立,所以  <1
<1
说明:此题运用了|x|<a x2<a2这一等价条件将绝对值符号去掉,并采用了求差比较法证明其等价不等式的正确性,并用到了绝对值的有关性质,也体现了证明不等式的方法的综合性和灵活性
x2<a2这一等价条件将绝对值符号去掉,并采用了求差比较法证明其等价不等式的正确性,并用到了绝对值的有关性质,也体现了证明不等式的方法的综合性和灵活性
例4 设|a|<1, |b|<1 求证|a+b|+|a-b|<2
证明:当a+b与a-b同号时,|a+b|+|a-b|=|a+b+a-b|=2|a|<2
当a+b与a-b异号时,|a+b|+|a-b|=|a+b-(a-b)|=2|b|<2
∴|a+b|+|a-b|<2
例5 已知 当a¹b时 求证:
当a¹b时 求证:
证法一:


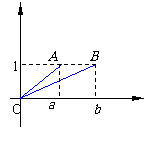 证法二:(构造法)如图
证法二:(构造法)如图 ,
,
 ,由三角形两边之差小于第三边得
,由三角形两边之差小于第三边得

定理:
证明:∵
 ①
①
又∵a=a+b-b |-b|=|b|
由①|a|=|a+b-b|≤|a+b|+|-b| 即|a|-|b|≤|a+b| ②
综合①②: 
注意:1° 左边可以“加强”同样成立,即
2° 这个不等式俗称“三角不等式”-三角形中两边之和大于第三边,两边之差小于第三边
3° a,b同号时右边取“=”,a,b异号时左边取“=”
推论1: ≤
≤
推论2:
证明:在定理中以-b代b得:
即 
前面我们已学过不等式的性质和证明方法,这一节我们再来研究一些含有绝对值的不等式的证明问题
我们知道,当a>0时,
|x|<a -a<x<a,
-a<x<a,
|x|>a x>a或x<-a
x>a或x<-a
根据上面的结果和不等式的性质,我们可以推导出含有绝对值的不等式具有下面的性质
4.状语从句的强调
not until引导的时间状语从句和because引导的原因状语从句可用于强调句型。句型构成分别是:"It was not until ... that ..."和"It is/was because ... that..."。
3.状语从句的成分省略
在时间、条件、原因、让步、方式等状语从句中,当从句的主语与主句的主语相同,且从句中含有be动词时,我们可将从句的主语(或作主语的代词it)连同be动词一起省略。
2.状语从句的语气 (见虚拟语气)
(1)as if /as though引导的从句以及if only.。.(但愿,要是……就好了)句子的虚拟情况:用一般过去时表示对现在的虚拟,用过去完成时表示对过去的虚拟。
(2)if引导的非真实条件句中的虚拟情况。
1.状语从句的时态
(1)当主句是一般将来时时,在时间、条件、让步等状语从句中用一般现在时表示将来的时间。
(2)when, before, after引导的从句的动作与主句动作的先后关系:若主从句的动作先后发生在过去,通常先发生的动作用过去完成时表示,后发生的动作用一般过去时。before, after本身已能表达动作的先后关系,所以在含有before, after从句的句子中,主从句的动作都可用一般过去时。
5."(should)+动词原形"用于其他名词性从句中。
(1)在It is ordered/desired/decided/requested/suggested/advised that.。.句型中,主语从句的谓语动词用"(should)+动词原形"。
(2)在It is necessary/ important/ strange/ natural that.。.句型中,主语从句的谓语动词用"(should)+动词原形"。
(3) 在advice, idea, order, plan, demand, proposal, suggestion, request等名词之后的表语从句或同位语从句中,谓语用"(should)+动词原形"。如:
My suggestion is that we (should) walk home instead of taking a taxi.
我的建议是我们走着回去,不用坐出租车。
通过锦囊十:状语从句中的时态、语气、强调和成分省略问题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com